Antihermitische (of antihermitische) matrix

Op deze pagina zie je wat een antihermitische matrix, ook wel antihermitische matrix genoemd, is. Je vindt voorbeelden van anti-Hermitische matrices, al hun eigenschappen en de vorm van dit soort complexe vierkante matrices. Ten slotte vindt u de uitleg over hoe u een complexe matrix kunt ontbinden in de som van een anti-Hermitische matrix plus een andere Hermitische matrix.

Wat is een antihermitische of antihermitische matrix?

Een anti-Hermitische matrix , of ook wel een anti-Hermitische matrix genoemd, is een vierkante matrix met complexe getallen waarvan de geconjugeerde transpositie gelijk is aan dezelfde matrix maar met een ander teken.

$A^*=-A$

Goud

$A^*$

is de getransponeerde geconjugeerde matrix van

$A$

Uit nieuwsgierigheid wordt dit type matrix zo genoemd omdat het voldoet aan de tegenovergestelde voorwaarde van de Hermitische matrix , wiens naam komt van de belangrijke Franse wiskundige Charles Hermite, een 19e-eeuwse professor en onderzoeker in de wiskunde die belangrijke studies maakte, onder meer in het gebied van de lineaire algebra.

Voorbeelden van antihermitische matrices

Zodra we de definitie van antihermitische matrix (of antihermitische matrix) hebben gezien, zullen we enkele voorbeelden zien van antihermitische matrices met verschillende dimensies:

Voorbeeld van een anti-Hermitische matrix van orde 2×2

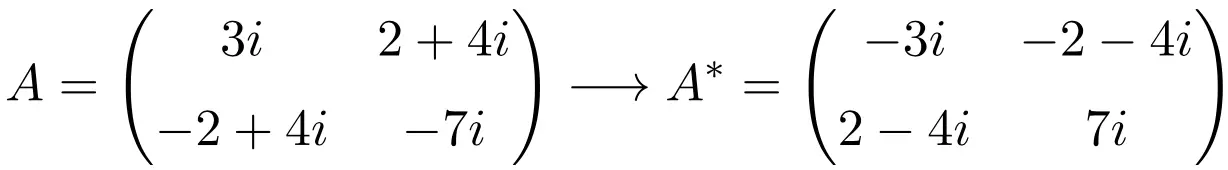
antihermitische of antihermitische matrix van afmeting 2x2

Voorbeeld van een antihermitische matrix met afmeting 3×3

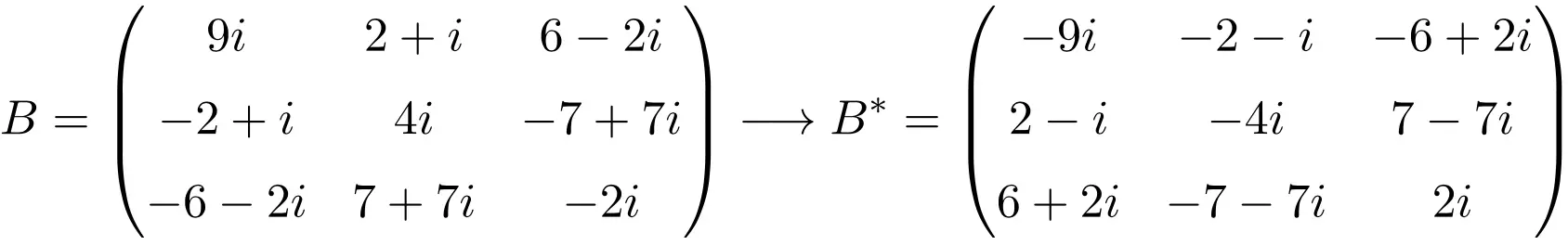
antihermitische of antihermitische matrix van dimensie 3x3

Voorbeeld van een anti-hermitische matrix van maat 4×4

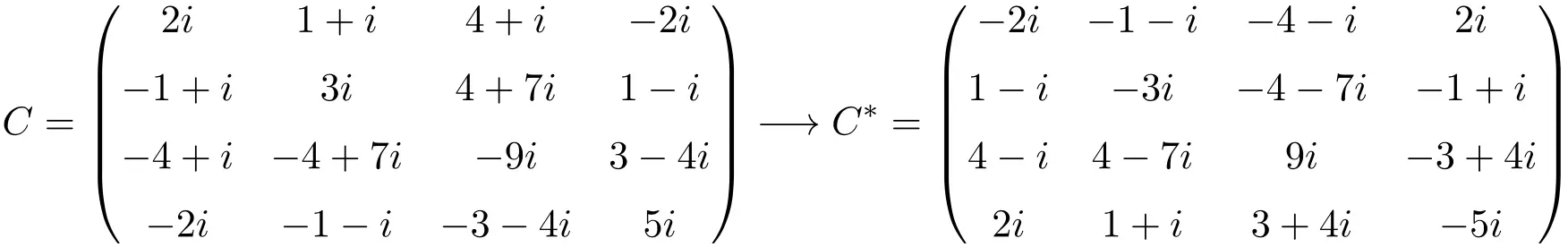
antihermitische of antihermitische matrix met afmeting 4x4

Zoals je kunt zien, zijn de matrices A, B en C anti-Hermitisch omdat de geconjugeerde getransponeerde matrix van elk gelijk is aan de matrix zelf, maar waarbij alle elementen van teken zijn veranderd.

Structuur van een antihermitische matrix

Als je al naar de voorgaande voorbeelden hebt gekeken, hebben anti-Hermitische matrices altijd dezelfde structuur: ze bestaan uit denkbeeldige getallen (zonder reëel deel) op de hoofddiagonaal, en het complexe element op de i-de lijn en de j-de lijn. lijn. kolom moet hetzelfde imaginaire deel en hetzelfde reële deel hebben, maar met een ander teken dan het element van de j-de rij en de i-de kolom.

Hoewel dit misschien een beetje ingewikkeld lijkt, wordt het zeker beter begrepen aan de hand van het volgende voorbeeld:

Structuur van een antihermitische matrix met afmeting 2×2

$\displaystyle \begin{pmatrix} ai & b+ci\\[1.1ex]-b+ci & di \end{pmatrix}$

Zoals je kunt zien, zijn de elementen van de hoofddiagonaal van een anti-Hermitische matrix volledig denkbeeldig en hebben de elementen van de secundaire diagonaal hetzelfde denkbeeldige deel en is het reële deel van teken veranderd.

Daarom moet het reële deel van een anti-Hermitische matrix antisymmetrisch zijn en het imaginaire deel symmetrisch.

Eigenschappen van de antihermitische matrix

We zullen nu zien wat de eigenschappen van dit type vierkante complexe matrix zijn:

Elke antihermitische matrix is een voorbeeld van een normale matrix . Hoewel niet alle normale matrices antihermitische matrices zijn.

Elke anti-hermitische matrix is diagonaliseerbaar. Bovendien bevat de resulterende diagonale matrix alleen puur denkbeeldige elementen.

Daarom zijn de eigenwaarden (of eigenwaarden) van een anti-Hermitische matrix altijd denkbeeldige getallen.

Op dezelfde manier zijn de eigenvectoren (of eigenvectoren) van verschillende eigenwaarden van een anti-Hermitische matrix orthogonaal.

Een matrix van reële getallen, dat wil zeggen dat geen enkel element een imaginair deel heeft, is anti-hermitisch als en slechts als het een antisymmetrische matrix is.

Een anti-hermitische matrix kan worden uitgedrukt als de som van een echte antisymmetrische matrix en een denkbeeldige symmetrische matrix .

$A =B+Ci$

De som (of aftrekking) van twee anti-Hermitische matrices is gelijk aan een andere anti-Hermitische matrix.

Het resultaat van het product van een anti-Hermitische matrix en een scalair is een andere anti-Hermitische matrix als de scalair een reëel getal is.

De kracht van een anti-Hermitische matrix is gelijk aan een anti-Hermitische matrix als de exponent oneven is; aan de andere kant, als het wordt verhoogd tot een even exponent, zal het resultaat een Hermitische matrix zijn.

Ja
$A$

een antihermitische matrix is, dan is het product

$iA$

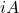
is een Hermitische matrix.

Ontleding van een complexe matrix in een anti-Hermitische matrix en een Hermitische matrix

Elke matrix die complexe getallen bevat, kan worden ontleed in de som van een anti-Hermitische matrix plus een andere Hermitische matrix . Maar hiervoor moet je de volgende kenmerken van dit soort matrices kennen:

De som van een vierkante complexe matrix plus zijn getransponeerde conjugaat is equivalent aan een Hermitische (of Hermitische) matrix:

$C + C^* = \text{Matriz Hermitiana}$

Het verschil tussen een vierkante complexe matrix en het getransponeerde conjugaat is gelijk aan een anti-hermitische matrix:

$C - C^* = \text{Matriz Antihermitiana}$

Daarom kunnen alle complexe matrices worden ontleed in de som van een Hermitische matrix en een anti-Hermitische matrix. Deze stelling staat bekend als de Teoplitz-ontbinding :

$\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}$

Waar C de complexe matrix is die we willen ontleden, is C* het getransponeerde conjugaat, en tenslotte zijn A en B respectievelijk de Hermitische en anti-Hermitische matrices waarin de matrix C wordt ontleed.

Wat is een antihermitische of antihermitische matrix?

Voorbeelden van antihermitische matrices

Structuur van een antihermitische matrix

Eigenschappen van de antihermitische matrix

Ontleding van een complexe matrix in een anti-Hermitische matrix en een Hermitische matrix

Laat een reactie achter Reactie annuleren