Analytische geometrie in de ruimte (formules)

Op deze pagina vind je de uitleg van alles over analytische meetkunde in de ruimte (en de formules): de vergelijkingen van de lijn en het vlak, de relatieve posities tussen vlakken en lijnen, hoe afstanden en hoeken berekend worden in de ruimte,…

Wat is geometrie in de ruimte?

Ruimtegeometrie is de tak van de geometrie die verantwoordelijk is voor het bestuderen van driedimensionale (3D) geometrische figuren, dat wil zeggen figuren die een plaats in de ruimte innemen. Zoals de kegel, de kubus, de piramide, de bol, de cilinder, de prisma’s, de veelvlakken, enz.

Op deze pagina zullen we ons echter concentreren op analytische geometrie in de ruimte , het deel van de ruimtegeometrie dat zich richt op de analyse van punten, lijnen, vlakken, de afstanden tussen twee geometrische figuren, de hoek die ze vormen, de snijpunten tussen verschillende geometrieën figuren. elementen, enz.

Vergelijkingen van de lijn in de ruimte

Bedenk dat de wiskundige definitie van een lijn een reeks opeenvolgende punten is die in dezelfde richting worden weergegeven, zonder krommen of hoeken.

Om elke lijn in een driedimensionale ruimte wiskundig uit te drukken (in R3) gebruiken we dus de vergelijkingen van de lijn, en om ze te vinden hebben we alleen een punt nodig dat bij de lijn hoort en de richtingsvector van die lijn.

Met alleen deze twee geometrische elementen kun je absoluut alle verschillende vergelijkingen van de lijn vinden, die als volgt zijn:

De vergelijkingen van de lijn zijn de vectorvergelijking , de parametervergelijkingen , de continue vergelijking en de impliciete (of algemene) vergelijking .

Hieronder vindt u een uitleg van de verschillende soorten vergelijkingen van de lijn.

Vectorvergelijking van lijn in de ruimte

Ja

is de richtingsvector van de lijn en

een punt dat hoort bij rechts:

De formule voor de vectorvergelijking van de lijn is:

Parametrische vergelijkingen van de lijn in de ruimte

We kunnen de formule voor de parametrische vergelijking van een lijn verkrijgen uit de vectorvergelijking door component aan component gelijk te stellen:

Continue vergelijking van de lijn in de ruimte

De formule voor de continue vergelijking van de lijn is:

Dit type vergelijking van de lijn kan ook worden verkregen uit parametrische vergelijkingen, je kunt de demonstratie op onze pagina van de continue vergelijking zien, daarnaast kun je ook voorbeelden zien en oefenen met opgeloste oefeningen van vergelijkingen aan de rechterkant.

Algemene (of impliciete) vergelijkingen van de lijn in de ruimte

Door tenslotte de fracties van de continue vergelijking van de lijn twee bij twee te vermenigvuldigen, verkrijgen we de algemene (of impliciete) vergelijkingen van de lijn :

Dit type vergelijking van de lijn wordt ook wel een cartesiaanse vergelijking genoemd.

We hebben zojuist de vier meest relevante vergelijkingen van de lijn gezien (vector, parametrisch, continu en algemeen), maar er is nog een enigszins bijzondere vergelijking en daarom kost het een hele pagina om deze uit te leggen. Dit is de canonieke vergelijking . In deze link kun je de hele uitleg ervan zien, waarom deze zo speciaal is en wat hem anders maakt dan alle anderen.

Vlakvergelijkingen in de ruimte

In de analytische meetkunde is de vergelijking van een vlak een vergelijking waarmee elk vlak analytisch kan worden uitgedrukt. Om de vergelijking van een vlak te vinden heb je dus alleen een punt en twee lineair onafhankelijke vectoren nodig die bij dat vlak horen.

Alle soorten vergelijkingen van het vlak zijn dus: de vectorvergelijking , de parametrische vergelijkingen , de impliciete (of algemene) vergelijking en de canonieke (of segmentale) vergelijking van het vlak.

Vervolgens zullen we de uitleg en formule van alle vergelijkingen van het plan zien.

Vectorvergelijking van het vlak

Gegeven een punt en twee richtingsvectoren van een vlak:

De formule voor de vectorvergelijking van een vlak is:

Of gelijkwaardig:

Goud

En

Het zijn twee scalairen, dat wil zeggen twee reële getallen.

Parametrische vergelijkingen van het vlak

Aan de andere kant is de formule voor de parametervergelijking van het vlak :

Impliciete of algemene vergelijking van het vlak

De impliciete vergelijking van een plan, ook wel de algemene vergelijking genoemd, wordt verkregen door de volgende determinant op te lossen en het resultaat op 0 te zetten:

De impliciete of algemene vergelijking van het resulterende plan zal dus de volgende vorm hebben:

Dit type vlakvergelijking wordt ook wel een cartesiaanse vlakvergelijking genoemd.

Canonieke of segmentale vergelijking van het vlak

De formule voor de canonieke of segmentale vergelijking van een vlak is als volgt:

Goud:

• 

  Dit is het snijpunt tussen het vlak en de X-as.

• 

  Dit is het snijpunt tussen het vlak en de Y-as.

• 

  Dit is waar het vlak de Z-as snijdt.

Vector normaal voor een vliegtuig

De vector loodrecht op een vlak is een vector die loodrecht staat op alle lijnen in dit vlak. Daarom betekent een vector die loodrecht op een vlak staat, dat deze loodrecht op het vlak staat.

Veel metrische problemen in de ruimtelijke analytische meetkunde hebben betrekking op vlakken en hun normaalvectoren. Om deze oefeningen op te lossen, hoef je alleen maar de wiskundige relatie tussen een vlak en zijn normaalvector te kennen:

De componenten X, Y, Z van de vector loodrecht op een vlak vallen respectievelijk samen met de coëfficiënten A, B, C van de impliciete (of algemene) vergelijking van dat vlak.

Goud

is de vector loodrecht op het vlak

Relatieve posities van twee geometrische elementen in de ruimte

Het is duidelijk dat een lijn of een vlak niet noodzakelijkerwijs alleen in de ruimte hoeft te zijn, maar integendeel, ze interageren normaal gesproken met elkaar: ze snijden elkaar, zijn evenwijdig, staan loodrecht, enz. Welnu, in deze sectie zullen we de verschillende relatieve posities van lijnen en vlakken zien en hoe deze worden bepaald.

Relatieve positie van twee lijnen in de ruimte

In de analytische meetkunde zijn er bij het werken in een driedimensionale ruimte (in R3) 4 mogelijke relatieve posities tussen twee lijnen: twee lijnen kunnen samenvallende lijnen , evenwijdige lijnen , secanslijnen of secanslijnen zijn.

Hoe u de relatieve positie van twee lijnen kunt vinden op basis van bereiken

Eén manier om de relatieve positie van twee rijen te vinden is door de bereiken van twee specifieke matrices te berekenen, zoals we hieronder zullen zien. Deze methode is erg handig wanneer de twee lijnen worden uitgedrukt in de vorm van een impliciete (of algemene) vergelijking.

Dus als we twee lijnen hebben uitgedrukt met hun impliciete (of algemene) vergelijkingen in een driedimensionale ruimte (in R3):

Laat A de matrix zijn die is samengesteld uit de coëfficiënten van de twee lijnen:

En gegeven de uitgebreide matrix A’, de matrix gevormd uit alle parameters van de twee lijnen:

Vervolgens kan de relatieve positie van de twee lijnen worden bepaald door de omvang van de twee voorgaande matrices volgens de volgende tabel:

Om de relatieve positie tussen twee rijen te vinden, zullen we daarom de bereiken van beide matrices moeten berekenen en afhankelijk van het bereik van elke matrix zal het het ene of het andere geval zijn.

Deze stelling kan worden bewezen met behulp van de stelling van Rouché-Frobenius (een methode die wordt gebruikt om stelsels van lineaire vergelijkingen op te lossen), maar op deze pagina zullen we het bewijs niet doen omdat het nogal omslachtig is en niet veel toevoegt. .

Relatieve positie van twee vlakken in de ruimte

In de analytische meetkunde zijn er slechts drie mogelijke relatieve posities tussen twee vlakken: snijdende vlakken, evenwijdige vlakken en samenvallende vlakken.

• Snijvlakken : twee vlakken snijden elkaar als ze elkaar maar op één lijn snijden.
• Parallelle vlakken : Twee vlakken zijn evenwijdig als ze elkaar op geen enkel punt snijden.
• Samenvallende vlakken : twee vlakken vallen samen als ze alle punten gemeenschappelijk hebben.

Hoe de relatieve positie van twee vlakken te bepalen aan de hand van coëfficiënten

Eén manier om de relatieve positie tussen twee vlakken te kennen, is door de coëfficiënten van hun algemene (of impliciete) vergelijkingen te gebruiken.

Beschouw dan de algemene (of impliciete) vergelijking van twee verschillende vlakken:

De relatieve positie tussen de twee vlakken in een driedimensionale ruimte hangt af van de evenredigheid van hun coëfficiënten of parameters:

De twee vlakken zullen elkaar dus snijden wanneer een van de coëfficiënten A, B of C niet evenredig is met de andere. Aan de andere kant zullen de twee vlakken evenwijdig zijn als alleen de onafhankelijke termen niet proportioneel zijn. En ten slotte zullen de plannen samenvallen als alle coëfficiënten van de twee vergelijkingen proportioneel zijn.

Afstanden in de ruimte

Hieronder vind je de formules om de afstand tussen verschillende geometrische elementen te berekenen: tussen een punt en een lijn, tussen twee vlakken, tussen een vlak en een lijn,…

Afstand tussen twee punten

De afstand tussen twee punten komt overeen met de norm van de vector die door deze 2 punten wordt bepaald.

Dus als we twee algemene punten hebben:

De formule voor de afstand tussen de twee punten is:

Afstand van een punt tot een lijn

De formule voor het berekenen van de afstand van een punt tot een lijn in de ruimte is:

Goud:

• 

  is de module van de richtingsvector van de lijn

  

• 

  is een punt aan de rechterkant

  

  

  een punt op de lijn

  

  En

  

  de vector gedefinieerd door de twee punten

• 

  is de modulus van het vectorproduct tussen de vectoren

  

  En

  

Afstand tussen twee lijnen

De afstand tussen twee lijnen hangt af van hun relatieve positie:

• Als de twee lijnen samenvallen of elkaar snijden , is de afstand tussen de twee lijnen gelijk aan nul, aangezien ze elkaar (minstens) op één punt snijden.
• Wanneer de twee lijnen evenwijdig zijn of elkaar snijden, moet afhankelijk van het geval een formule worden toegepast (beide verklaringen zijn hieronder beschikbaar).

Afstand tussen twee parallelle lijnen

Twee evenwijdige lijnen liggen altijd op dezelfde afstand van elkaar. Dus om de afstand tussen twee parallelle lijnen in de ruimte (in R3) te berekenen, gebeurt dit op dezelfde manier als in het vlak (in R2): je hoeft alleen maar een punt op een van de twee lijnen te nemen en daar de afstand te vinden Het is van dit punt naar de andere lijn.

Om de afstand tussen 2 evenwijdige lijnen te bepalen, moet je dus de formule voor de afstand tussen een punt en een lijn gebruiken.

Afstand tussen twee snijdende lijnen

Laat de richtingsvector en elk punt van twee snijdende lijnen zijn:

De formule voor de afstand tussen twee snijdende lijnen is:

Goud:

• 

  is de absolute waarde van het gemengde product van de vectoren

  

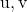
  en de vector gedefinieerd door de punten

  

  En

  

  .

• 

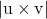
  is de modulus van het vectorproduct tussen de richtingsvectoren van de twee gekruiste lijnen.

Hoewel je hier de formule hebt, is het bepalen van de afstand tussen twee kruisende lijnen ingewikkelder dan het lijkt. Dus als je wilt oefenen, kun je in de volgende link voorbeelden en opgeloste oefeningen zien over de afstand tussen twee kruisende lijnen.

Afstand van een punt tot een vlak

Gegeven een punt en de algemene (of impliciete) vergelijking van een vlak:

De formule voor de afstand van een punt tot een vlak is:

Als we door toepassing van de formule een resultaat verkrijgen dat gelijk is aan nul, betekent dit uiteraard dat de afstand tussen het punt en het vlak nul is en dat het punt daarom deel uitmaakt van dit vlak.

Afstand tussen twee vlakken

De afstand tussen twee vlakken in de ruimte hangt af van de relatieve positie tussen deze twee vlakken:

• Als de twee vlakken elkaar snijden of samenvallen , is de afstand ertussen gelijk aan nul omdat ze elkaar op een bepaald punt snijden.
• Als de twee vlakken evenwijdig zijn, wordt de afstand tussen de twee vlakken berekend door een punt op een van de twee vlakken te nemen en de afstand tussen dat punt en het andere vlak te berekenen.

Afstand tussen twee evenwijdige vlakken

Twee evenwijdige vlakken bevinden zich altijd op dezelfde afstand van elkaar, dus om de afstand tussen twee evenwijdige vlakken te vinden, kunnen we een punt op een van de twee vlakken nemen en de afstand vanaf dat punt tot het andere vlak berekenen.

Om de afstand tussen twee evenwijdige vlakken te berekenen, moet je dus een punt op een van de twee vlakken vinden en vervolgens de formule gebruiken voor de afstand tussen een punt en een vlak.

Hoeken in de ruimte

Net als bij afstanden hangt het bepalen van de hoek tussen twee geometrische objecten in de ruimte af van hun geometrische kenmerken. Omdat het berekenen van de hoek gevormd door twee lijnen niet hetzelfde is als het berekenen van de hoek gevormd door twee vlakken. Dus hieronder heb je de formules om de hoeken tussen lijnen en vlakken te vinden.

Hoek tussen twee lijnen

Om de hoek tussen twee lijnen in de Euclidische ruimte te kennen, moeten we de hoek berekenen die wordt gevormd door hun richtingsvectoren, daarom:

Gegeven de richtingsvectoren van twee verschillende lijnen:

De hoek gevormd door deze twee lijnen kan worden berekend met de volgende formule:

Goud

En

zijn de modules van de vectoren

En

respectievelijk.

Bedenk dat de formule voor de modulus van een vector is:

Hoek tussen twee vlakken

De hoek tussen twee vlakken is gelijk aan de hoek gevormd door de normaalvectoren van die vlakken. Om de hoek tussen twee vlakken te vinden, berekenen we daarom de hoek gevormd door hun normaalvectoren, aangezien ze equivalent zijn .

Gegeven de algemene (of impliciete) vergelijking van twee verschillende vlakken:

De normaalvector van elk vlak is:

En de hoek gevormd door deze twee vlakken wordt bepaald door de hoek te berekenen die wordt gevormd door hun normaalvectoren met behulp van de volgende formule:

Hoek tussen een lijn en een vlak

De hoek gevormd door een lijn en een vlak wordt gedefinieerd als de kleinste van de twee complementaire hoeken gevormd door de richtingsvector van de lijn en de normaalvector van het vlak.

Daarom, als

is de richtingsvector van de lijn en

is de vector loodrecht op het vlak:

De formule die wordt gebruikt om de hoek te berekenen die wordt gevormd door een lijn en een vlak is: