Hier vindt u hoe de afstand van een lijn tot een vlak wordt berekend en bovendien ziet u voorbeelden en oefeningen die stap voor stap worden opgelost.
Wat is de afstand tussen een lijn en een vlak?
In de analytische meetkunde hangt de afstand tussen een lijn en een vlak in de ruimte af van de relatieve positie tussen deze twee geometrische elementen:
- Als de lijn in het vlak ligt of als de lijn en het vlak evenwijdig zijn , is de afstand tussen hen nul.
- Als de lijn evenwijdig is aan het vlak , wordt de afstand van de lijn tot het vlak bepaald door een willekeurig punt op de lijn te nemen en de afstand vanaf dat punt tot het vlak te berekenen.
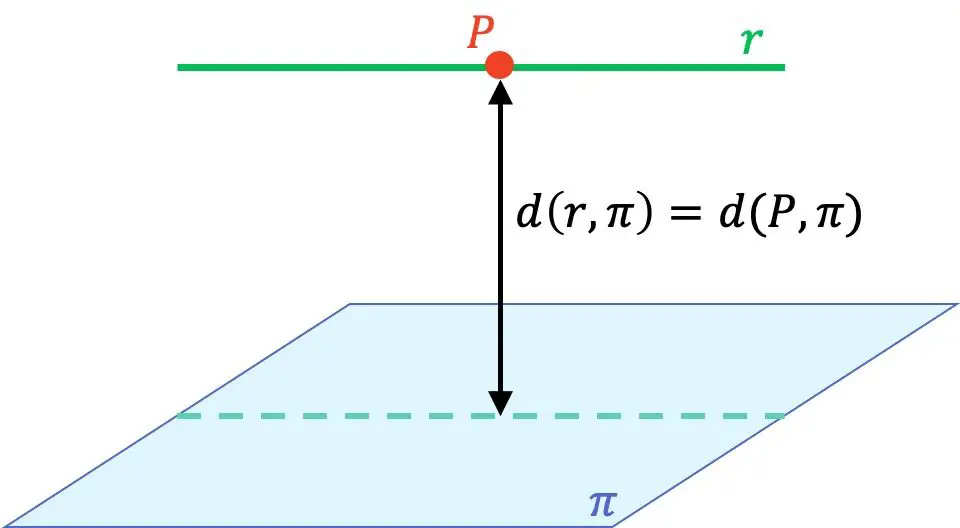
Om de afstand van een lijn tot een vlak te berekenen, is het daarom essentieel dat u weet hoe u de relatieve positie tussen een lijn en een vlak kunt bepalen en hoe u de afstand tussen een punt en een vlak kunt berekenen. Bent u dus niet helemaal duidelijk of kent u de formules niet, dan raden wij u aan eerst eens een kijkje te nemen op de gelinkte pagina’s, waar u stap voor stap uitleg, voorbeelden en opgeloste oefeningen vindt.
Voorbeeld van het berekenen van de afstand tussen een lijn en een vlak
Zodat je kunt zien hoe je de afstand tussen een lijn en een vlak in de ruimte kunt vinden (in R3), zullen we als voorbeeld een probleem oplossen:
- Hoe ver is de lijn
in het vliegtuig
?
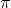
![\displaystyle r: \ \begin{cases}x=-2+t \\[1.7ex] y=1-3t \\[1.7ex] z=-1+2t\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4785f2386b4ff9387b56cf8c5645c62d_l3.png "Rendered by QuickLaTeX.com")
Om de afstand tussen de lijn en het vlak te vinden, moet u eerst de relatieve positie tussen de twee kennen.
Aan de ene kant wordt de lijn gedefinieerd in de vorm van parametrische vergelijkingen, dus de richtingsvector en het punt waar hij doorheen gaat zijn:
![\displaystyle r: \ \begin{cases} \vv{\text{v}}_r =(1,-3,2) \\[2ex] P(-2,1,-1) \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0765b71f9eead3b644fd5de150cdf321_l3.png "Rendered by QuickLaTeX.com")
En aan de andere kant is de vector loodrecht op het vlak:
Om de relatieve positie tussen het vlak en de lijn te bepalen, is het dus noodzakelijk om het scalaire product te berekenen tussen de richtingsvector van de lijn en de vector loodrecht op het vlak:
![\begin{aligned} \vv{\text{v}}_r \cdot \vv{n} & = (1,-3,2) \cdot (4,2,1) \\[2ex] & = 1 \cdot 4-3 \cdot 2 +2\cdot 1 \\[2ex] &= 4 -6 +2 \\[2ex] & = 0\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-39d2d450c32a6fdf3182a3d16cc18116_l3.png "Rendered by QuickLaTeX.com")
Het resultaat van het puntproduct is nul, dus de lijn kan alleen in het vlak liggen of evenwijdig daaraan zijn. Om erachter te komen welk geval het is, vervangen we de cartesische coördinaten van het punt op de lijn in de vergelijking van het vlak:
Door het punt van de lijn in de vergelijking van het vlak te vervangen, verkrijgen we een ongelijkheid; daarom respecteert het punt de vergelijking van het vlak niet en zijn de lijn en het vlak dus evenwijdig.
Zodra we weten dat de lijn en het vlak evenwijdig zijn, kunnen we nu de geometrische afstand daartussen berekenen. Om dit te doen, nemen we het punt op de lijn en berekenen we de afstand vanaf dat punt tot het vlak.
We gebruiken dus de formule voor de afstand van een punt tot een vlak:
Nu vervangen we de waarde van elke onbekende in de formule:
En ten slotte voeren we de bewerkingen uit:
Zodat de afstand tussen de lijn en het vlak gelijk is aan de berekende afstand tussen het punt en het vlak:
Het is duidelijk dat afstand ons altijd een positieve waarde moet geven, omdat afstanden altijd positief zijn. Als we een negatief resultaat krijgen, betekent dit dat we een fout hebben gemaakt bij het zetten van een stap.