Afstand tussen een punt en een lijn

Hier vindt u de formule waarmee u de afstand tussen een punt en een lijn kunt berekenen. Daarnaast zul je verschillende voorbeelden en opgeloste oefeningen kunnen zien van afstanden tussen punten en lijnen en zelfs de toepassingen die deze operatie heeft (bijvoorbeeld het vinden van de afstand tussen parallelle lijnen).

Formule voor de afstand tussen een punt en een lijn

De afstand tussen een punt en een lijn is de kortste afstand tussen dat punt en de lijn. Wiskundig gezien is deze minimale afstand gelijk aan de lengte van het segment dat van het punt naar de lijn wordt getrokken en dat loodrecht op de lijn staat.

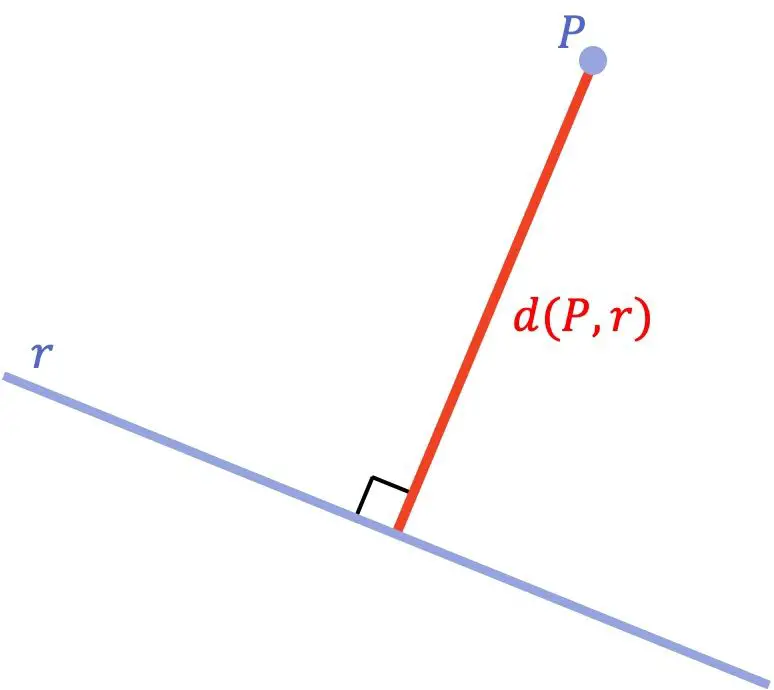
wat is de afstand tussen een punt en een lijn

Als we eenmaal het geometrische concept van de afstand tussen een punt en een lijn hebben gezien, gaan we kijken wat de formule is die wordt gebruikt om die afstand te berekenen:

Gegeven de impliciete (of algemene) vergelijking van een lijn en de coördinaten van elk punt op een vlak:

$r: \ Ax+By+C=0 \qquad \qquad P(p_x,p_y)$

De formule voor de afstand tussen een punt en een lijn is:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Belangrijk: Merk op dat de vergelijking van de lijn in de formule de vorm heeft van een impliciete (of algemene) vergelijking, dus als we de lijn in een ander type vergelijking hebben uitgedrukt, moeten we deze eerst doorgeven aan de impliciete vergelijking en dan we kunnen de formule toepassen.

Voorbeeld van het berekenen van de afstand tussen een punt en een lijn

Hieronder ziet u een voorbeeld van het berekenen van de afstand tussen een punt en een lijn:

Zoek de afstand tussen het punt
$P$

en de wet

$r:$

$P(2,-1) \qquad \qquad r: \ 3x+4y-5=0$

Om de afstand tussen het punt en de lijn te berekenen, past u eenvoudig de formule toe:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Nu vervangen we elke term door zijn waarde:

$d(P,r)= \cfrac{\lvert 3\cdot 2 + 4\cdot (-1)-5\rvert}{\sqrt{3^2+4^2}}$

En tenslotte berekenen we de afstand:

$d(P,r)= \cfrac{\lvert 6 -4-5\rvert}{\sqrt{9+16}} =\cfrac{\lvert -3 \rvert}{\sqrt{25}} = \mathbf{\cfrac{3}{5}}$

Afstand tussen twee parallelle lijnen

Een van de toepassingen van het berekenen van de afstand tussen een lijn en een punt is het vinden van de afstand tussen evenwijdige lijnen.

Om het concept te begrijpen dat we hieronder zullen uitleggen, moet je uiteraard weten wat parallelle lijnen zijn , dus als je de definitie ervan niet precies weet, laten we een link achter waar we het in detail uitleggen en kun je ook voorbeelden zien van evenwijdige lijnen.

Om de afstand tussen twee parallelle lijnen te vinden, neemt u eenvoudigweg een punt op een van de twee lijnen en berekent u de afstand vanaf dat punt tot de andere lijn.

Om de afstand tussen twee parallelle lijnen te bepalen, wordt dus ook de formule voor de afstand tussen een lijn en een punt gebruikt.

Aan de andere kant, als we bij het gebruik van de formule een afstand van 0 eenheden krijgen, betekent dit dat de lijnen elkaar op een bepaald punt raken en dat de lijnen daarom niet evenwijdig zijn, maar elkaar snijden, samenvallen of loodrecht staan. Als je wilt, kun je op onze website de verschillen tussen dit soort lijnen bekijken.

Laten we dus eens kijken hoe we een afstandsprobleem tussen twee parallelle lijnen kunnen oplossen aan de hand van een voorbeeld:

Bereken de afstand tussen de volgende twee evenwijdige lijnen:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

Het eerste wat we moeten doen is een punt op een van de lijnen krijgen (degene die je wilt). In dit geval berekenen we een punt op de lijn

$s.$

Om dit te doen, moet u een waarde aan een van de variabelen geven, zoals wij dat bijvoorbeeld zullen doen

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

En nu wissen we de andere variabele (

$y$

) van de verkregen vergelijking om te weten hoeveel het op dit punt waard is:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Daarom wordt het punt verkregen uit de lijn

$s$

Oosten:

$P(0,-2)$

En zodra we al een punt op een lijn hebben, berekenen we de afstand van dat punt tot de andere lijn met behulp van de formule:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{2}{\sqrt{20}}=\bm{0,45}$

Problemen met de afstand tussen een punt en een lijn opgelost

Oefening 1

Bereken de afstand tussen het punt

$P$

en de wet

$r:$

$P(4,2) \qquad \qquad r: \ 5x-3y+6=0$

zie oplossing

Om de afstand tussen een punt en een lijn te vinden, past u eenvoudigweg de formule toe:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

We vervangen elke term door de waarde ervan en berekenen de afstand:

$d(P,r)= \cfrac{\lvert 5\cdot 4 + (-3)\cdot 2+6\rvert}{\sqrt{5^2+(-3)^2}}=\cfrac{20}{\sqrt{34}}= \bm{3,43}$

Oefening 2

Wat is de afstand tussen het punt

$P$

en de wet

$r$

$P(-3,-1) \qquad \qquad r: \ y=-3x+5$

zie oplossing

In dit geval heeft de vergelijking van de lijn een impliciete (of algemene) vorm. Om de formule voor de afstand van een punt tot een lijn te gebruiken, moet de lijn in plaats daarvan worden uitgedrukt als een impliciete vergelijking. We moeten daarom eerst de lijn transformeren en doorgeven aan een impliciete vergelijking (geef gewoon alle termen aan dezelfde kant van de vergelijking door):

$r: \ 3x+y-5=0$

En zodra de lijn al een expliciete vorm heeft, kunnen we nu de formule gebruiken voor de afstand tussen een punt en een lijn:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

We vervangen daarom elke term door de waarde ervan en berekenen de afstand:

$d(P,r)= \cfrac{\lvert 3\cdot (-3) + 1\cdot (-1)-5\rvert}{\sqrt{3^2+1^2}}=\cfrac{\lvert -9-1-5\rvert}{\sqrt{9+1}}=\cfrac{15}{\sqrt{10}}= \bm{4,74}$

Oefening 3

Wat is de afstand tussen de volgende twee lijnen?

$r: \ x+3y-4=0 \qquad \qquad s: \ 2x+6y+6=0$

zie oplossing

Eerst zullen we verifiëren dat dit twee parallelle lijnen zijn. Hiervoor de coëfficiënten van de variabelen

$x$

$y$

moeten evenredig zijn aan elkaar, maar niet aan de onafhankelijke termen:

$\cfrac{1}{2} = \cfrac{3}{6}\neq \cfrac{-4}{6} \ \longrightarrow \ \text{Paralelas}$

De lijnen zijn inderdaad evenwijdig, we kunnen daarom de procedure toepassen.

Nu moeten we een punt uit een van de lijnen halen (degene die je wilt). In dit geval berekenen we een punt op de lijn

$s.$

Om dit te doen, moet u een waarde aan een van de variabelen toekennen, wat wij bijvoorbeeld zullen doen

$x=0:$

$2x+6y+6=0 \ \xrightarrow{x \ = \ 0} \ 2\cdot 0+6y+6=0$

En nu wissen we de andere variabele (

$y$

) van de verkregen vergelijking om de waarde ervan op dit punt te kennen:

$6y=-6$

$y= \cfrac{-6}{6}$

$y= -1$

Zodat het punt wordt verkregen uit de lijn

$s$

Oosten:

$P(0,-1)$

Zodra we een punt op een lijn kennen, berekenen we de afstand van dat punt tot de andere lijn met de formule:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 1\cdot 0 + 3\cdot (-1) +(-4)\rvert}{\sqrt{1^2+3^2}}= \cfrac{7}{\sqrt{10}}=\bm{2,21}$

Oefening 4

Bereken de waarde van het onbekende

$k$

zodat de afstand tussen het punt

$P$

en de wet

$r$

dat wil zeggen 5 eenheden.

$P(-2,5) \qquad \qquad r: \ 12x-5y+k=0$

zie oplossing

We moeten eerst de formule voor de afstand tussen een punt en een lijn toepassen:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Nu vervangen we elke term door zijn waarde en vereenvoudigen we de uitdrukking:

$d(P,r)= \cfrac{\lvert 12\cdot (-2) + (-5)\cdot 5+k\rvert}{\sqrt{12^2+(-5)^2}}= \cfrac{\lvert -24-25+k\rvert}{\sqrt{169}}=\cfrac{\lvert -49+k\rvert}{13}$

De probleemstelling vertelt ons dat de afstand tussen het punt en de lijn gelijk moet zijn aan 5, dus we stellen de vorige uitdrukking gelijk aan 5:

$\cfrac{\lvert -49+k\rvert}{13}=5$

En we lossen de resulterende vergelijking op. In de teller van de breuk zit een absolute waarde. Daarom moeten we afzonderlijk analyseren wanneer de absolute waarde positief is en wanneer deze negatief is:

$\cfrac{+(-49+k)}{13}=5$