Hoe de snijpunten van een functie met de assen te berekenen

Op deze pagina wordt uitgelegd wat de snijpunten (of kruisingen) zijn van een functie met de cartesiaanse assen en hoe u deze kunt berekenen. Daarnaast vindt u verschillende voorbeelden om volledig te begrijpen hoe ze worden gevonden en kunt u zelfs oefenen met oefeningen die stap voor stap worden opgelost.

Wat zijn de snijpunten (of snijpunten) van een functie met de assen?

Voordat we zien hoe ze worden berekend, moeten we onthouden wat de snijpunten zijn van een functie met de assen.

Snijpunten of snijpunten van de as zijn de punten waar de weergave van een functie de coördinaatassen snijdt, dat wil zeggen de punten in de grafiek die op de X-as en op de l-as samenkomen. Y-as.

De parabool in de volgende grafiek snijdt bijvoorbeeld de Y-as op punt (0,3) en snijdt de X-as op punten (-1,0) en (3,0).

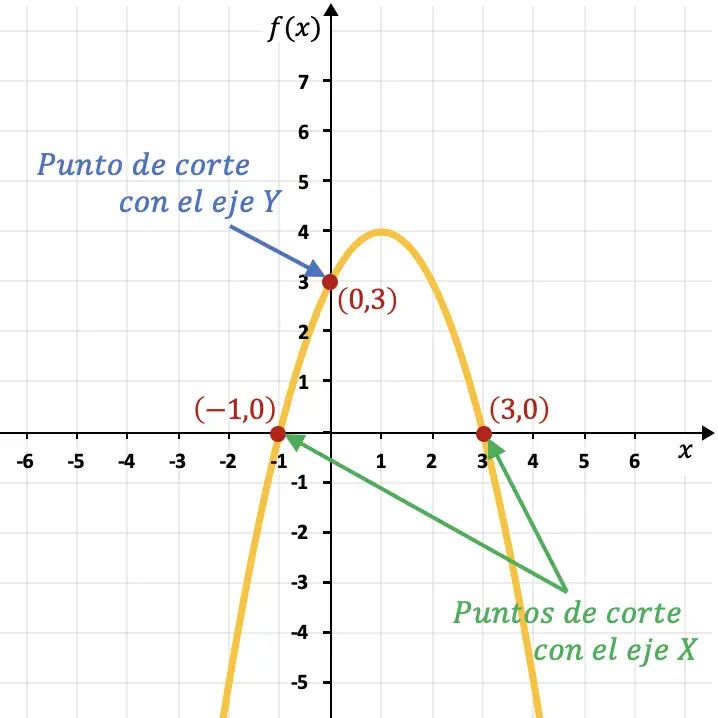
Snij- of snijpunten van een functie met de assen

Snijpunt van een functie met de X-as

De tweede coördinaat van de snijpunten van een functie met de X-as is altijd 0, dus:

De afkappunten van elke x-asfunctie OX hebben de vorm

$(a,0)$

, en kan worden berekend door de volgende vergelijking op te lossen:

$f(x)=0$

Soms kunnen we bij het oplossen van deze vergelijking twee (of meer) oplossingen krijgen, dit betekent dat de functie de X-as twee (of meer) keer snijdt. Aan de andere kant, als de vergelijking geen oplossing heeft, impliceert dit dat de functie de X-as niet snijdt.

Snijpunt van een functie met de Y-as

De eerste coördinaat van de snijpunten van een functie met de Y-as is altijd 0, dus:

Het afkappunt van elke functie met de y-as OY heeft de vorm

$(0,a)$

, en kan worden gevonden door de afbeelding van de functie op x=0 te berekenen:

$f(0)$

In tegenstelling tot breekpunten op de X-as kan er slechts één breekpunt op de Y-as zijn.

Voorbeeld van het berekenen van de afkappunten van een functie met de assen

Om ervoor te zorgen dat u geen twijfels heeft, zullen we hieronder een voorbeeld zien van hoe u de snijpunten van een functie met de cartesiaanse assen kunt vinden:

Zoek numeriek de afkappunten van de volgende functie:

$f(x)=-2x+4$

We zullen eerst het afkappunt van de functie berekenen met de x-as. Het snijpunt met de X-as zal altijd de tweede component gelijk hebben aan 0, dat wil zeggen van het type zijn

$(a,0)$

. Omdat f(x) altijd gelijk is aan 0 op de OX-as. Om de andere component van het punt te vinden, moeten we de vergelijking oplossen

$f(x)=0:$

$f(x)=0$

$-2x+4=0$

$-2x=-4$

$x=\cfrac{-4}{-2}=2$

Het snijpunt met de X-as is dus:

$\bm{(2,0)}$

Nu gaan we het snijpunt met de y-as vinden. Het snijpunt met de Y-as zal altijd de eerste component gelijk hebben aan 0, dat wil zeggen dat het punt van het type zal zijn

$(0,a)$

. Omdat de onafhankelijke variabele x altijd op de Y-as vervalt. Om de andere coördinaat van het punt te vinden, moeten we dus berekenen

$f(0):$

$f(0)=-2 \cdot 0+4=4$

Het snijpunt met de Y-as is dus:

$\bm{(0,4)}$

Hieronder heb je de voorbeeldfunctie grafisch weergegeven, je kunt zien dat de gevonden drempels overeenkomen met die in de grafiek:

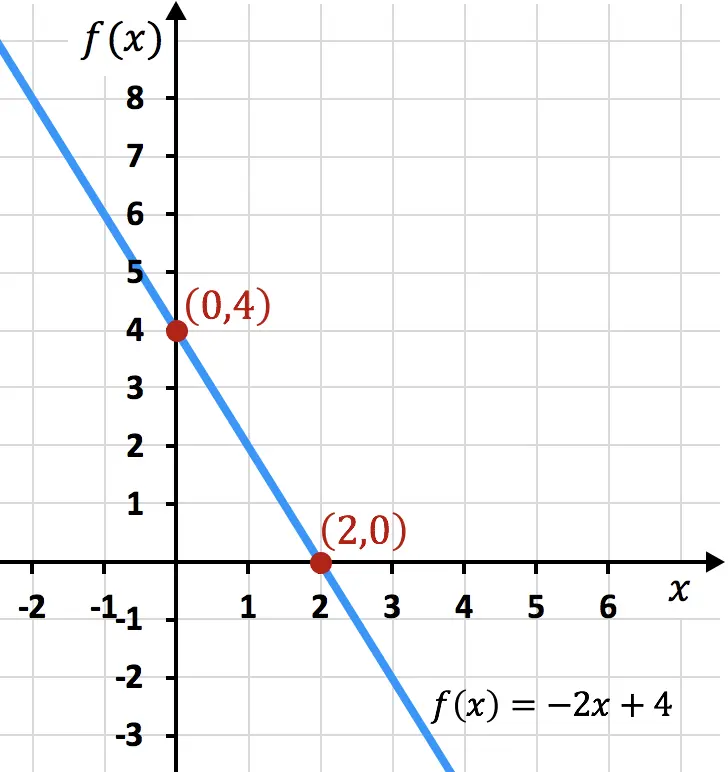
hoe je de snijpunten van een functie met assen kunt vinden

Opgeloste oefeningen voor snijpunten van een functie met assen

Oefening 1

Bepaal de snijpunten met de coördinaatassen van de volgende functie:

$f(x)=3x-3$

Zie de oplossing

Snijpunt met X-as

Om het snijpunt van de functie met de X-as te vinden, is het noodzakelijk om op te lossen

$f(x)=0:$

$f(x)=0$

$3x-3=0$

$3x=3$

$x=\cfrac{3}{3}=1$

Het snijpunt van de functie met de X-as is daarom:

$\bm{(1,0)}$

Snijpunt met Y-as

Om het snijpunt met de Y-as te vinden, moet u berekenen

$f(0):$

$f(0)=3\cdot 0 -3= -3$

Het snijpunt van de functie met de Y-as is daarom:

$\bm{(0,-3)}$

Oefening 2

Zoek de snijpunten met de cartesische assen van de volgende affiene functie:

$f(x)=2x+8$

Zie de oplossing

Snijpunt met X-as

Om het limietpunt van de functie met de OX-as te vinden, moeten we de functie gelijk stellen aan nul en de resulterende vergelijking oplossen:

$f(x)=0$

$2x+8=0$

$2x=-8$

$x=\cfrac{-8}{2}=-4$

Het snijpunt van de functie met de abscis-as is dus:

$\bm{(-4,0)}$

Snijpunt met Y-as

Om het afkappunt met de OY-as te vinden, moeten we berekenen

$f(0):$

$f(0)=2\cdot 0 +8= 8$

Het snijpunt van de functie met de computeras is daarom:

$\bm{(0,8)}$

Oefening 3

Bereken de afkappunten met de assen van de volgende kwadratische functie:

$f(x)=x^2-3x+2$

Zie de oplossing

Snijpunt met X-as

Om het snijpunt van de functie met de X-as te vinden, is het noodzakelijk om op te lossen

$f(x)=0:$

$f(x)=0$

$x^2-3x+2=0$

In dit geval moeten we een kwadratische vergelijking oplossen, dus passen we de formule toe:

$\displaystyle x =\cfrac{-b \pm \sqrt{b^2 -4ac}}{2a}$

$\displaystyle x=\cfrac{ -(-3) \pm \sqrt{(-3)^2-4\cdot 1 \cdot 2}}{2\cdot 1} = \cfrac{3 \pm 1}{2} = \begin{cases} 2 \\[2ex] 1 \end{cases}$

We hebben twee oplossingen van de kwadratische vergelijking verkregen, dus de functie snijdt de X-as op twee punten:

$\bm{(1,0)} \qquad \bm{(2,0)}$

Snijpunt met Y-as

Aan de andere kant is het noodzakelijk om te berekenen om het snijpunt met de Y-as te bepalen

$f(0):$

$f(0)=0^2-3\cdot 0+2= 2$

Daarom is het enige snijpunt van de functie met de Y-as:

$\bm{(0,2)}$

Oefening 4

Zoek de snijpunten met de assen van het cartesiaanse vlak van de volgende rationale functie:

$f(x)=\cfrac{5}{x}$

Zie de oplossing

Snijpunt met X-as

Om het snijpunt van de functie met de X-as te vinden, is het noodzakelijk om op te lossen

$f(x)=0:$

$f(x)=0$

$\cfrac{5}{x}=0$

$5=0\cdot x$

$5=0$

$5\neq 0$

5 is niet equivalent aan 0, dus de vergelijking heeft geen oplossing en daarom is er geen snijpunt tussen de functie en de X-as.

Snijpunt met Y-as

Om het snijpunt met de Y-as te vinden, moet u berekenen

$f(0):$

$f(0)=\cfrac{5}{0}= \infty$

Elk getal gedeeld door nul is een onbepaaldheid die oneindigheid oplevert. Daarom reikt de functie op geen enkel punt verder dan de Y-as.

Kortom, de oefenfunctie heeft geen snijpunten met de assen , dat wil zeggen dat de grafiek op geen enkel punt door de X-as of de Y-as gaat.

Oefening 5

Bereken de afkappunten met de assen van de volgende derdegraadsfunctie:

$f(x)=x^3-9x$

Zie de oplossing

Snijpunt met X-as

Om het snijpunt van de functie met de X-as te vinden, is het noodzakelijk om op te lossen

$f(x)=0:$

$f(x)=0$

$x^3-9x=0$

Beide termen van de vergelijking hebben een x , waarmee we een gemeenschappelijke factor kunnen extraheren:

$x(x^2-9)=0$

Om aan de vorige gelijkheid te voldoen, moet een van de factoren 0 zijn. Daarom stellen we elke factor gelijk aan nul om alle mogelijke oplossingen te verkrijgen:

$\displaystyle x(x^2-9)=0 \ \longrightarrow \begin{cases} \bm{x = 0} \\[2ex] x^2-9 = 0\ \longrightarrow \ x^2=9 \ \longrightarrow \ \bm{x=\pm 3} \end{cases}$

We hebben daarom drie oplossingen van de derdegraadsvergelijking verkregen, dus de functie snijdt de X-as in 3 punten:

$\bm{(-3,0)} \qquad \bm{(0,0)} \qquad \bm{(3,0)}$

Snijpunt met Y-as

Om het snijpunt met de Y-as te berekenen, moet u berekenen

$f(0):$

$f(0)=0^3-9\cdot 0 = 0$

Daarom is het enige snijpunt van de functie met de Y-as de coördinaatoorsprong (0,0):

$\bm{(0,0)}$

Merk op dat we dit punt al hadden gevonden bij de berekening van het snijpunt met de X-as, omdat de functie op dit punt met beide assen tegelijkertijd snijdt.

Wat zijn de snijpunten (of snijpunten) van een functie met de assen?

Snijpunt van een functie met de X-as

Snijpunt van een functie met de Y-as

Voorbeeld van het berekenen van de afkappunten van een functie met de assen

Opgeloste oefeningen voor snijpunten van een functie met assen

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Laat een reactie achter Reactie annuleren