▷ Afgeleide van een product (formule en opgeloste oefeningen)

In dit artikel leggen we uit hoe je het product van twee functies kunt afleiden (formule). Daarnaast kun je verschillende voorbeelden zien van afgeleiden van producten van functies en zelfs oefenen met opgeloste oefeningen over vermenigvuldigingsderivaten.

Formule voor de afgeleide van een product

De afgeleide van een product van twee verschillende functies is gelijk aan het product van de afgeleide van de eerste functie door de tweede ongedifferentieerde functie plus het product van de eerste ongedifferentieerde functie door de afgeleide van de tweede functie.

Met andere woorden, als f(x) en g(x) twee verschillende functies zijn, is de formule voor de afgeleide van de vermenigvuldiging tussen de twee functies als volgt:

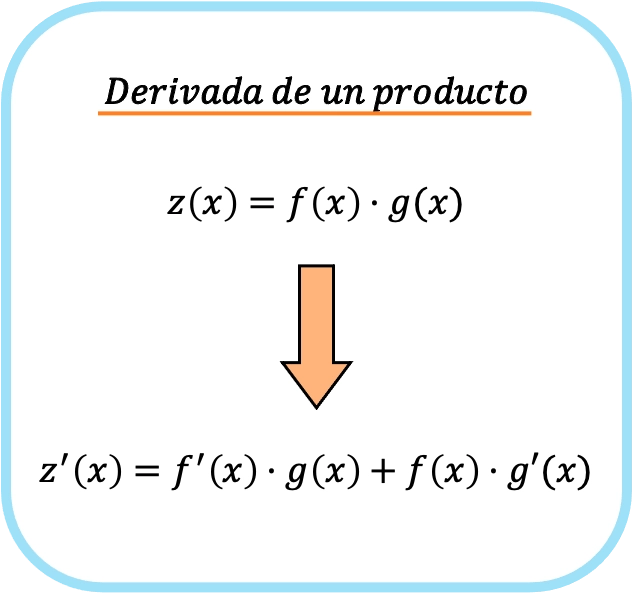
Door dus de regel van de afgeleide van een product toe te passen, gaan we van een eenvoudige vermenigvuldiging naar twee verschillende producten.

Voorbeelden van afgeleide producten

Zodra we weten wat de formule voor de afgeleide van een product (of vermenigvuldiging) is, zullen we verschillende voorbeelden van dit type afgeleide oplossen. Dit maakt het voor u veel gemakkelijker om te begrijpen hoe een product van twee functies wordt afgeleid.

voorbeeld 1

In dit voorbeeld lossen we de afgeleide van twee potentiële functies op door te vermenigvuldigen:

$f(x)=5x^2\cdot (x^3+4x-6)$

Zoals we in de vorige sectie hebben gezien, is de formule voor de afgeleide van vermenigvuldiging:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Daarom moeten we eerst de afgeleide van elke functie afzonderlijk berekenen:

$\cfrac{d}{dx}\ 5x^2=10x$

$\cfrac{d}{dx}\ (x^3+4x-6)=3x^2+4$

En zodra we de afgeleide van elke functie kennen, kunnen we de formule toepassen voor de afgeleide van het product van twee functies. Dat wil zeggen, we vermenigvuldigen de afgeleide van de eerste factor met de tweede factor zonder te differentiëren, en voegen vervolgens het product van de eerste factor toe zonder te differentiëren met de afgeleide van de tweede factor:

$\begin{array}{c}f(x)=5x^2\cdot (x^3+4x-6)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\end{array}$

Ten slotte voeren we de bewerkingen uit om het verkregen resultaat te vereenvoudigen:

$\begin{aligned}f'(x)& =10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\\[1.5ex] & = 10x^4+40x^2-60x +15x^4+20x^2 \\[1.5ex] & = 25x^4+60x^2-60x\end{aligned}$

Voorbeeld 2

In dit geval zullen we het product van een constante afleiden uit een functie:

$f(x)=7\cdot (x^2+3x)$

De afgeleide regel van een product is als volgt:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

We leiden dus afzonderlijk elke functie af die deel uitmaakt van het product:

$\cfrac{d}{dx}\ 7=0$

$\cfrac{d}{dx}\ (x^2+3x)=2x+3$

En dan passen we de regel toe voor de afgeleide van een vermenigvuldiging:

$\begin{array}{c}f(x)=7\cdot (x^2+3x)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=0\cdot (x^2+3x)+7\cdot (2x+3)=14x+21\end{array}$

Merk op dat de afgeleide van een constante altijd nul is, dus we kunnen afleiden dat de afgeleide van het vermenigvuldigen van een constante met een functie gelijk is aan het product van de constante en de afgeleide van de functie.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=k\cdot f(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=k\cdot f'(x)\end{array} \end{empheq}$

Voorbeeld 3

Laten we het product tussen een exponentiële functie en een natuurlijke logaritme oplossen:

$f(x)=4^{3x}\cdot \ln(x^2)$

De formule voor de afgeleide van een vermenigvuldiging van twee functies is:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

We moeten daarom eerst afzonderlijk de afgeleide maken van elke functie die het product vormt, die als volgt is:

$\cfrac{d}{dx}\ 4^{3x}=4^{3x}\cdot \ln (4) \cdot 3$

$\cfrac{d}{dx}\ \ln(x^2)=\cfrac{2x}{x^2}=\cfrac{2}{x}$

Het afgeleide product van de functies is daarom:

$\begin{array}{c}f(x)=4^{3x}\cdot \ln(x^2)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=4^{3x}\cdot \ln (4) \cdot 3\cdot \ln(x^2) +4^{3x}\cdot \cfrac{2}{x} \end{array}$

Opgeloste oefeningen over de afgeleide van een product

Leidt de volgende functieproducten af:

$\text{A) }f(x)=5\ln(3x)$

$\text{B) }f(x)=(4x^2+1)(6x^3-7)$

$\text{C) }f(x)=\text{cos}(4x)\cdot e^{x^2}$

$\text{D) }f(x)=(3x^3-4x^2+8x)\cdot \sqrt{6x^2+3x}$

$\text{E) }f(x)=5^{4x}\cdot \log_9(x^3-x)$

$\text{F) }f(x)=\left(10x^6-6x^5\right)^4\cdot \text{arcsen}(x^2+9x)$

Zie de oplossing

$\text{A) } f'(x)=5\cdot \cfrac{3}{3x} =\cfrac{5}{x}$

$\begin{aligned}\text{B) }f'(x)&=8x\cdot (6x^3-7)+(4x^2+1)\cdot 18x^2\\[1.2ex]&=48x^4-56x+72x^4+18x^2\\[1.2ex]&=120x^4+18x^2-56x \end{aligned}$

$\text{C) }f'(x) =-4\text{sen}(4x)\cdot e^{x^2}+\text{cos}(4x)\cdot e^{x^2}\cdot 2x$

$\text{D) }f'(x)=(9x^2-8x+8)\cdot \sqrt{6x^2+3x}+(3x^3-4x^2+8x)\cdot\cfrac{12x+3}{2\sqrt{6x^2+3x}}$

$\text{E) }f'(x)=5^{4x}\cdot \ln(5) \cdot 4 \cdot \log_9(x^3-x)+ 5^{4x}\cdot\cfrac{3x^2-1}{(x^3-x)\ln(9)}$

$\begin{aligned}\text{F) }f'(x)=& 4\left(10x^6-6x^5\right)^3\cdot (60x^5-30x^4)\cdot \text{arcsen}(x^2+9x)\ +\\[1.2ex] &+\left(10x^6-6x^5\right)^4\cdot \cfrac{2x+9}{\sqrt{1-\left(x^2+9x\right)^2}}\end{aligned}$

Afgeleid van een product met drie functies

Vervolgens laten we u de formule achter voor de afgeleide van het vermenigvuldigen van 3 functies, aangezien deze sterk lijkt op die van 2 functies en in sommige gevallen nuttig kan zijn.

De afgeleide van een product van drie functies is gelijk aan het product van de afgeleide van de eerste functie en de andere twee functies, plus het product van de afgeleide van de tweede functie en de andere twee functies, plus het product van de afgeleide van de derde functie.functie door de andere twee functies.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=1mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=f(x)\cdot g(x)\cdot h(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)\cdot h(x)+f(x)\cdot g'(x)\cdot h(x)+f(x)\cdot g(x)\cdot h'(x)\end{array} \end{empheq}$

Als we bijvoorbeeld de volgende vermenigvuldiging van drie verschillende functies willen afleiden:

$f(x)=3x\cdot e^{2x} \cdot \text{sen}(x)$

Om de afgeleide op te lossen, moeten we de regel van de afgeleide van het product van drie functies toepassen, daarom:

$f'(x)=3\cdot e^{2x} \cdot \text{sen}(x)+3x\cdot 2e^{2x} \cdot \text{sen}(x)+3x\cdot e^{2x} \cdot \text{cos}(x)$

Demonstratie van de formule voor de afgeleide van een product

Ten slotte zullen we de formule demonstreren voor de afgeleide van een vermenigvuldiging. Je hoeft het niet uit je hoofd te leren, maar het is altijd goed om te begrijpen waar de formules vandaan komen. 🙂

Uit de wiskundige definitie van de afgeleide:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Laat de functie z het product zijn van twee verschillende functies:

$z(x)=f(x)\cdot g(x)$

Dan zal de afgeleide van z volgens de definitie zijn:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)\cdot g(x+h)\bigr]-\bigl[f(x)\cdot g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x)\cdot g(x)}{h}$

Zoals we weten, heeft het toevoegen van een term door optellen en aftrekken geen invloed op het resultaat, zolang beide dezelfde term zijn. We kunnen daarom doorgaan naar de volgende stap:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)\color{orange}\bm{-f(x+h)\cdot g(x)+f(x+h)\cdot g(x)}\color{black}-f(x)\cdot g(x)}{h}$

We gebruiken nu de grenseigenschappen om de vorige grens in twee verschillende grenzen te scheiden:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x+h)\cdot g(x)}{h}+\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x)}{h}$

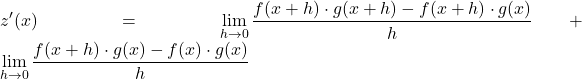
We extraheren de gemeenschappelijke factor in de teller van de twee breuken:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\bigl(g(x+h)-g(x)\bigr)}{h}+\lim_{h \to 0}\frac{g(x)\bigl(f(x+h)-f(x)\bigr)}{h}$

Aan de andere kant kennen we het resultaat van de volgende limiet:

$\displaystyle \lim_{h \to 0}f(x+h)=f(x)$

We kunnen daarom de limieten vereenvoudigen:

$\displaystyle z'(x)=\lim_{h \to 0}f(x+h)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+\lim_{h \to 0}g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

$\displaystyle z'(x)=f(x)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Als we tenslotte naar de twee resterende limieten kijken, komt elk overeen met de definitie van de afgeleide van een functie. Gelijkheid kan daarom worden vereenvoudigd:

$\displaystyle z'(x)=f(x)\cdot g'(x)+g(x)\cdot f'(x)$

Of gelijkwaardig:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x) \end{empheq}$

Afgeleide van een product (of vermenigvuldiging)

Formule voor de afgeleide van een product

Voorbeelden van afgeleide producten

voorbeeld 1

Voorbeeld 2

Voorbeeld 3

Opgeloste oefeningen over de afgeleide van een product

Afgeleid van een product met drie functies

Demonstratie van de formule voor de afgeleide van een product

Laat een reactie achter Reactie annuleren