Hier ontdekt u hoe u de secans van een functie kunt afleiden. Bovendien kunt u stap voor stap verschillende oefeningen zien die zijn opgelost op de afgeleide van de secans. En tot slot vind je de demonstratie van de formule voor dit type trigonometrische afgeleide.
Wat is de afgeleide van de secans?
De afgeleide van de secans van x is gelijk aan het product van de secans van x en de tangens van x.
![]()
Door trigonometrische formules toe te passen, kan de afgeleide van de secans van x ook worden gedefinieerd als het quotiënt van de sinus van x gedeeld door het kwadraat van de cosinus van x.
![]()
En als we de kettingregel toepassen, is de afgeleide van de secans van een functie het product van de secans van de functie maal de tangens van de functie maal de afgeleide van de functie.
![]()
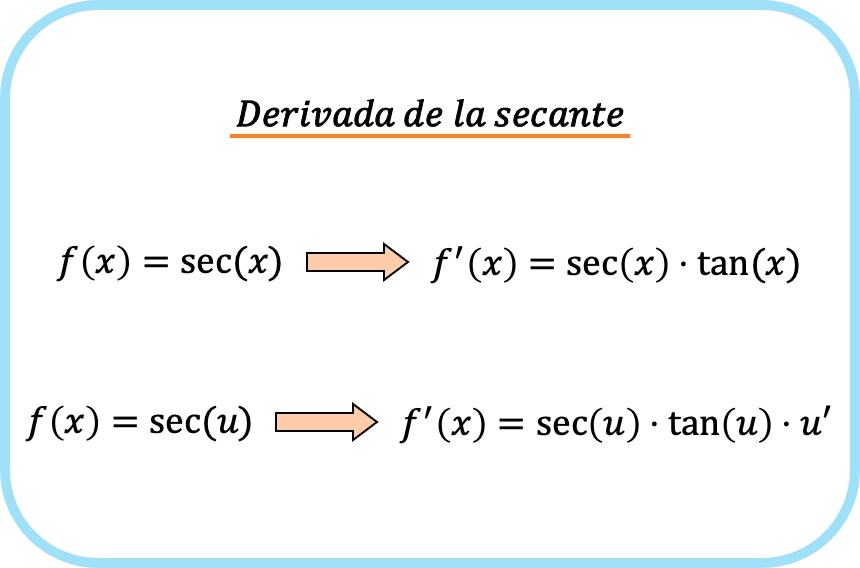
Samenvattend is de formule voor de afgeleide van de secansfunctie als volgt:
Voorbeelden van afgeleide van de secans
Zodra we hebben gezien wat de formule voor de afgeleide van de secans is, zullen we verschillende voorbeelden van dit soort trigonometrische derivaten oplossen.
Voorbeeld 1: Afgeleide van de secans van 2x
In dit voorbeeld zullen we zien hoeveel de afgeleide van de secans van 2x waard is:
![]()
Om de secans van de functie 2x af te leiden, moet u de bijbehorende formule gebruiken. Bovendien hebben we in het secansargument een andere functie dan x, dus moeten we de kettingregel toepassen.
![]()
De functie 2x is lineair, dus de afgeleide ervan is 2. Om de afgeleide te vinden, vervangen we daarom eenvoudigweg de u door 2x en de u’ door 2 in de formule:
![]()
Voorbeeld 2: Afgeleide van de secans van x kwadraat
In deze oefening zullen we zien wat de afgeleide is van de secans van x in het kwadraat:
![]()
Om de secans van een functie af te leiden, kun je een van de twee formules hierboven gebruiken, maar in dit geval zullen we de functie differentiëren met de formule voor vermenigvuldiging tussen de secans en de raaklijn.
![]()
De afgeleide van x tot de macht 2 geeft 2x, dus de afgeleide van de secans van x in het kwadraat is:
![]()
Voorbeeld 3: Afgeleide van de secanskubus van een polynoom
![]()
De regel voor de afgeleide van de secans van een functie is:
![]()
Maar in dit geval moeten we een samengestelde functie afleiden, aangezien de secans tot de derde macht wordt verheven en bovendien hebben we in zijn argumentatie een polynomiale functie. Om de hele functie te differentiëren, moeten we dus de kettingregel toepassen:
![Rendered by QuickLaTeX.com \begin{aligned}f'(x)& =3\text{sec}^2(x^5+4x^2-3)\text{sec}(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\\[1.5ex]&=3\text{sec}^3(x^5+4x^2-3)\text{tan}(x^5+4x^2-3)(5x^4+8x)\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7ab88cc23ab3fb559e2386cd52637082_l3.png)
Opgeloste oefeningen op de afgeleide van een secans
Leid de volgende secansfuncties af:
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{B) }f(x)& =4\text{sec}^3(5x^4)\cdot \text{sec}(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\\[1.5ex] &=4\text{sec}^4(5x^4)\cdot \text{tan}(5x^4)\cdot 20x^3\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-72985d8bce95d808b9070bc7b834b271_l3.png)
![]()
![]()
![]()
Demonstratie van de formule voor de afgeleide van de secans
Vervolgens zullen we de formule voor de afgeleide van de secans bewijzen. Hoewel het uiteraard niet nodig is om het bewijs uit je hoofd te kennen, is het altijd goed om te begrijpen waar de formules vandaan komen.
Wiskundig gezien is de definitie van de secans de multiplicatieve inverse van de cosinus:
![]()
Daarom kunnen we proberen de secans af te leiden met behulp van de quotiëntregel:
![]()
En zoals we in de eerste sectie hebben gezien, kan de vorige uitdrukking worden omgezet in de formule voor de afgeleide van de secans. Om dit te doen, scheiden we de breuk in twee verschillende breuken:
![]()
De deling van de sinus door de cosinus is equivalent aan de raaklijn, daarom vervangen we het genoemde quotiënt door de raaklijn:
![]()
Volgens de wiskundige definitie van de secansfunctie is de cosinus de inverse vermenigvuldiger. Dus door één gedeeld door de cosinus te vervangen door de secans, komen we tot de formule voor de afgeleide ervan:
![]()