Afgeleide van de hyperbolische cotangens

Hier leggen we uit hoe je de hyperbolische cotangens van een functie kunt afleiden. Je zult ook voorbeelden vinden van de afgeleide van de hyperbolische cotangens.

Formule voor de afgeleide van de hyperbolische cotangens

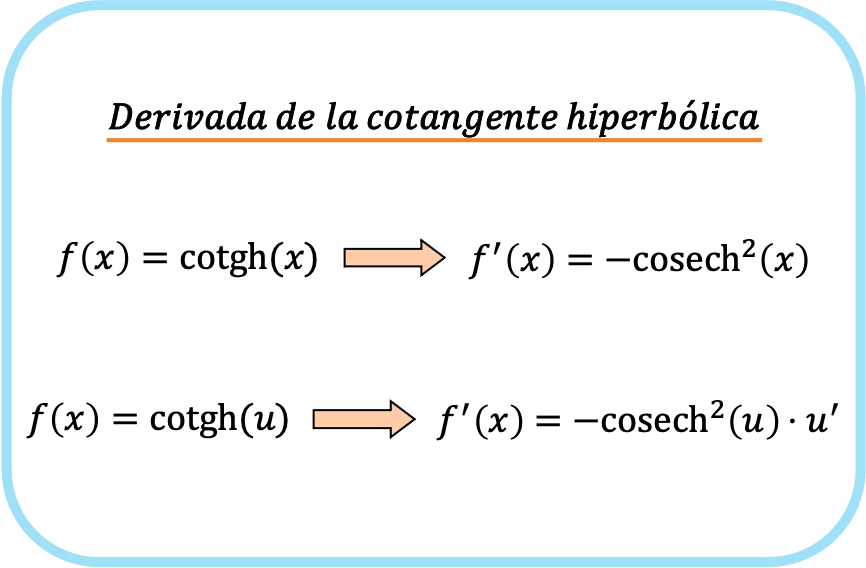
De afgeleide van de hyperbolische cotangens van x is gelijk aan minus de hyperbolische cosecans van x in het kwadraat.

f(x)=\text{cotgh}(x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(x)

Daarom is de afgeleide van de hyperbolische cotangens van een functie minus de hyperbolische cosecans van de functie maal de afgeleide van die functie.

f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'

Houd er rekening mee dat in de tweede formule de kettingregel is toegepast en dat deze formule wordt gebruikt als er een andere functie dan x voorkomt in het hyperbolische cotangens-argument.

afgeleid van de hyperbolische cotangens

In sommige wiskundeboeken zul je wellicht tegenkomen dat de afgeleide van de cotangens een andere is, aangezien de volgende drie uitdrukkingen gelijkwaardig zijn:

f'(x)=-\text{cosech}^2(x)=1-\text{cotgh}^2(x)=-\cfrac{1}{\text{senh}^2(x)}

Het is duidelijk dat je elke uitdrukking van de drie kunt gebruiken om de hyperbolische cotangens af te leiden, maar de meest gebruikte is de hyperbolische cosecans in het kwadraat.

Voorbeelden van afgeleide van de hyperbolische cotangens

Zodra we weten wat de formule is voor de afgeleide van de hyperbolische cotangens van een functie, zullen we verschillende voorbeelden van dit soort trigonometrische afgeleiden oplossen.

voorbeeld 1

In dit voorbeeld zullen we zien wat de afgeleide is van de hyperbolische cotangens van de functie 2x.

f(x)=\text{cotgh}(2x)

In het hyperbolische cotangens-argument hebben we een andere functie dan x, dus moeten we de formule met de kettingregel gebruiken om de afleiding uit te voeren:

f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'

Omdat 2x een term van de eerste graad is, is de afgeleide ervan 2. Om de afgeleide van de hyperbolische cotangens van 2x te vinden, plaatsen we eenvoudigweg 2x in het kwadraat van de cosecans hyperbolicus en vermenigvuldigen we met 2.

f(x)=\text{cotgh}(2x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(2x)\cdot 2

Voorbeeld 2

In het tweede voorbeeld zullen we de waarde bepalen van de afgeleide van de hyperbolische cotangens van een polynoomfunctie.

f(x)=\text{cotgh}(3x^4-5x)

Zoals we hierboven hebben gezien, is de regel voor het afleiden van de hyperbolische cotangens van een functie als volgt:

f(x)=\text{cotgh}(u)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(u)\cdot u'

Daarom zal de afgeleide van de hyperbolische cotangens van deze oefening als volgt zijn:

f(x)=\text{cotgh}(3x^4-5x)\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=-\text{cosech}^2(3x^4-5x)\cdot(12x^3-5)

Laat een reactie achter

Je e-mailadres wordt niet gepubliceerd. Vereiste velden zijn gemarkeerd met *

Scroll naar boven