Hier leest u hoe u de hyperbolische boogtangens van een functie kunt afleiden. Je zult ook opgeloste voorbeelden van dit soort trigonometrische afgeleiden kunnen zien en ten slotte zullen we je de formule laten zien voor de afgeleide van de hyperbolische boogtangens.
Formule voor de afgeleide van de hyperbolische boogtangens
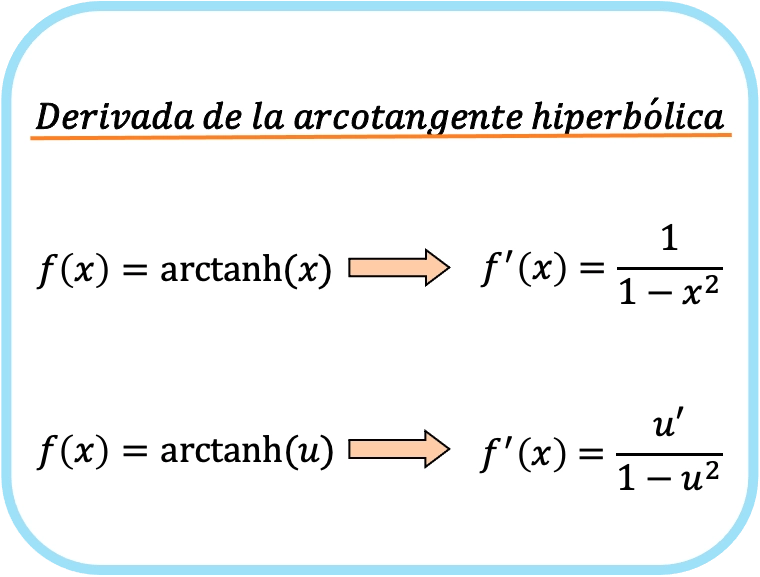
De afgeleide van de hyperbolische boogtangens van x is één gedeeld door één minus x kwadraat.
![]()
Daarom is de afgeleide van de hyperbolische boogtangens van een functie gelijk aan het quotiënt van de afgeleide van die functie gedeeld door één minus het kwadraat van de genoemde functie.
![]()
In feite zijn beide formules hetzelfde, maar in de tweede wordt de kettingregel toegepast. Als u x bijvoorbeeld vervangt door u, krijgt u precies de eerste formule, aangezien de afgeleide van x 1 is.
Net zoals boogtangens de inverse functie van tangens is, is hyperbolische boogtangens het omgekeerde van hyperbolische tangens. Toch zijn hun afgeleiden heel verschillend. Je kunt de afgeleide van deze trigonometrische functie hier bekijken:
➤ Zie: formule voor de afgeleide van de hyperbolische tangens
Voorbeelden van afgeleide van hyperbolische boogtangens
voorbeeld 1
![]()
Logischerwijs moeten we de regel van de afgeleide van de hyperbolische boogtangens toepassen:
![]()
De afgeleide van 2x is 2, dus zet een twee in de teller van de breuk en één min 2x kwadraat in de noemer:
![]()
Voorbeeld 2
![]()
Om de afgeleide van deze functie op te lossen, moeten we de formule gebruiken voor de afgeleide van de hyperbolische boogtangens.
![]()
Bovendien is de hyperbolische boogtangens-argumentfunctie een samengestelde functie, dus we zullen ook de kettingregel moeten toepassen:
![]()
Bewijs van de afgeleide van de hyperbolische boogtangens
In dit laatste deel zullen we de formule demonstreren voor de afgeleide van de hyperbolische boogtangens.
![]()
Omdat de hyperbolische boogtangens de inverse hyperbolische tangens is, kunnen we de vorige gelijkheid op een andere manier uitdrukken:
![]()
Nu differentiëren we beide kanten van de vergelijking:
![]()
Wij zuiveren u:
![]()
Aan de andere kant weten we dat het verschil tussen de kwadraten van de hyperbolische cosinus en de hyperbolische sinus 1 oplevert. We kunnen daarom de vorige uitdrukking omzetten in een breuk:
![]()
![]()
We delen alle termen van de breuk door het kwadraat van de hyperbolische cosinus:
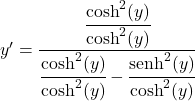
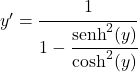
Het quotiënt van de hyperbolische sinus tussen de hyperbolische cosinus is gelijk aan de hyperbolische tangens, daarom:
![]()
![]()
Maar zoals we aan het begin van het bewijs zagen, is de hyperbolische tangens equivalent aan de variabele x. Daarom kunnen we de uitdrukking vervangen en zo de formule verkrijgen voor de afgeleide van de hyperbolische boogtangens:
![]()