▷ Ketenregel (afgeleiden): opgeloste oefeningen

Hier leert u wat kettingregel is en hoe u functies kunt afleiden met behulp van kettingregel. Daarnaast krijg je verschillende voorbeelden te zien van derivaten opgelost met de kettingregel en kun je zelfs oefenen met stapsgewijze opgeloste oefeningen over derivaten waarbij de kettingregel wordt toegepast.

Wat is de kettingregel?

De kettingregel is een formule die wordt gebruikt om samengestelde functies af te leiden. De kettingregel stelt dat de afgeleide van een samengestelde functie f(g(x)) gelijk is aan de afgeleide f'(g(x)) vermenigvuldigd met de afgeleide g'(x) .

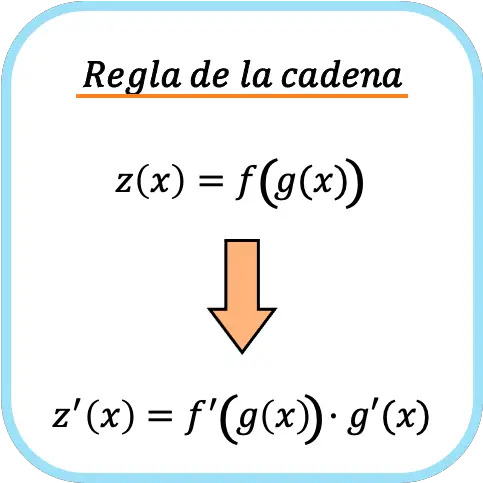
➤ Zie: samengestelde functie

Informeel wordt vaak gezegd dat de kettingregel bedoeld is om de functie te differentiëren en deze vervolgens te vermenigvuldigen met wat erin zit .

Met de kettingregelformule kunnen we samengestelde functies veel gemakkelijker differentiëren, omdat we, als we een samenstelling van functies zouden differentiëren met behulp van de limiet van de afgeleide definitie, veel berekeningen zouden moeten doen.

Aan de andere kant moet er rekening mee worden gehouden dat deze regel alleen wordt gebruikt om de afgeleide van samengestelde functies te vinden, en niet van enig type functie of bewerkingen met functies. Een veel voorkomende fout is bijvoorbeeld om het verkeerd te doen en de ketenregel toe te passen in functionele producten zoals de volgende:

$\ln(x)\cdot x^2$

❌

De kettingregel kan alleen worden gebruikt als we de ene functie binnen de andere hebben .

$\ln(x^2)$

✅

Voorbeelden van derivaten met de kettingregel

Gegeven de definitie van de kettingregel zullen we verschillende functies afleiden met de kettingregel als voorbeeld. Houd er rekening mee dat als u in een voorbeeld niet begrijpt hoe de functie wordt afgeleid met de kettingregel, u dit ons in de opmerkingen kunt vragen!

voorbeeld 1

In dit voorbeeld gebruiken we de kettingregel om de natuurlijke logaritme van x kwadraat af te leiden:

$f(x)=\ln(x^2)$

De afgeleide van de natuurlijke logaritme is gelijk aan 1 keer zijn argument, dus de afgeleide

$f'\bigl(g(x)\bigr)$

zijn:

$f(x)=\ln(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{u}$

$f\bigl(g(x)\bigr)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\cfrac{1}{x^2}$

Aan de andere kant is de afgeleide van x tot de macht twee 2x:

$g(x)=x^2\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=2x$

Ten slotte berekenen we de afgeleide van de gehele functie door de kettingregel toe te passen. De afgeleide van de samengestelde functie zal het product zijn van de twee afgeleiden die we zojuist hebben gevonden:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\ln(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{x^2}\cdot 2x = \cfrac{2x}{x^2}=\cfrac{2}{x}$

Voorbeeld 2

In dit tweede voorbeeld zullen we een potentiële functie afleiden op basis van een polynoom:

$f(x)=\left(3x^2+4x-5\right)^3$

Om een macht af te leiden, moeten we de oorspronkelijke exponent ervoor plaatsen en één eenheid van de exponent aftrekken, zodat de afgeleide van de potentiële functie zonder toepassing van de kettingregel zou zijn:

$f\bigl(g(x)\bigr)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=3\left(3x^2+4x-5\right)^2$

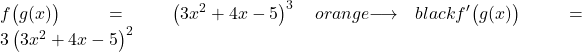
Nu leiden we af wat tussen haakjes staat:

$g(x)=3x^2+4x-5\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=6x+4$

En ten slotte gebruiken we de kettingregel om de afgeleide van de gehele functie op te lossen, wat de vermenigvuldiging zal zijn van de twee eerder berekende afgeleiden:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\left(3x^2+4x-5\right)^3 \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=3\left(3x^2+4x-5\right)^2\cdot (6x+4)$

Voorbeeld 3

In dit geval lossen we de sinusafgeleide van x in blokjes plus 7x op:

$f(x)=\text{sen}(x^3+7x)$

Het is inderdaad een samenstelling van functies omdat we de functie x ³ +7x binnen de sinusfunctie hebben, we kunnen daarom de kettingregel gebruiken om de afgeleide van de samengestelde functie te vinden.

Aan de ene kant is de afgeleide van de sinus de cosinus, dus de afgeleide van de externe functie zal de cosinus zijn met hetzelfde argument als de sinus:

$f\bigl(g(x)\bigr)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'\bigl(g(x)\bigr)=\text{cos}(x^3+7x)$

En aan de andere kant is de afgeleide van x ³ +7x 3x ² +7.

$g(x)=x^3+7x\quad\color{orange}\bm{\longrightarrow}\quad\color{black} g'(x)=3x^2+7$

Daarom is de afgeleide van de samengestelde functie het product van de twee afgeleiden:

$z(x)=f\bigl(g(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\text{sen}(x^3+7x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\text{cos}(x^3+7x)\cdot (3x^2+7)$

Opgeloste oefeningen over derivaten met de kettingregel

Oefening 1

Leid de volgende samengestelde functie af met behulp van de kettingregel:

$f(x)=\left(5x^2-6x\right)^3$

Zie de oplossing

De externe functie is een potentiële functie, dus om de afgeleide ervan te berekenen, moet u de volgende formule toepassen:

$f\bigl(g(x)\bigr)=a\bigl(g(x)\bigr)^n \ \longrightarrow \ f'\bigl(g(x)\bigr)=n\cdot a\bigl(g(x)\bigr)^{n-1}$

$f\bigl(g(x)\bigr)=\left(5x^2-6x\right)^3\ \longrightarrow \ f'\bigl(g(x)\bigr)= 3\left(5x^2-6x\right)^2$

En dan berekenen we de afgeleide van de functie binnenin. Het is een aftrekking van machten, dus om de afgeleide ervan te berekenen, moet je de volgende formule op elk van de termen toepassen:

$f(x)=ax^n \ \longrightarrow \ f'(x)=n\cdot ax^{n-1}$

$g(x)=5x^2-6x\ \longrightarrow$

$g'(x)=2\cdot 5x^1-1 \cdot 6 x^0 =10x-6$

Kortom, de afgeleide van de samengestelde functie is het product van de twee gevonden afgeleiden:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=\left(5x^2-6x\right)^3 \ \longrightarrow \ \bm{f'(x)= 3\left(5x^2-6x\right)^2\cdot (10x-6)}$

Oefening 2

Los de afgeleide van de volgende samengestelde functie op met behulp van de kettingregel:

$f(x)=-3\left(5x^5+9x^3\right)^4$

Zie de oplossing

Eerst vinden we de afgeleide van de externe functie:

$\begin{aligned} f\bigl(g(x)\bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr) & =4 \cdot ( -3) \left(5x^5+9x^3\right)^3 \\[1.5ex]&=-12\left(5x^5+9x^3\right)^3 \end{aligned}$

En nu lossen we de afgeleide van de interne functie op:

$g(x)=5x^5+9x^3\ \longrightarrow \ g'(x)=25x^4+27x^2$

De afgeleide van de gehele functie is daarom:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=-3\left(5x^5+9x^3\right)^4 \ \longrightarrow \ \bm{f'(x)=-12\left(5x^5+9x^3\right)^3\cdot \left(25x^4+27x^2\right)}$

Oefening 3

Bereken de afgeleide van de volgende samenstelling van functies met de kettingregel:

$f(x)=e^{2x^3}$

Zie de oplossing

Het is een exponentiële functie, dus om de afgeleide ervan te berekenen, moet u de volgende formule toepassen:

$f(x)=e^{x} \ \longrightarrow \ f'(x)=e^{x}$

$f\bigl(g(x)\bigr)=e^{2x^3} \ \longrightarrow \ f'\bigl(g(x)\bigr)= e^{2x^3}$

We maken ook onderscheid tussen de functie en de exponent van de functie:

$g(x)=2x^3 \ \longrightarrow \ g'(x)=6x^2$

En we gebruiken de kettingregel om de afgeleide van de samengestelde functie met gehele getallen te vinden:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=e^{2x^3} \ \longrightarrow \ \bm{f'(x)= e^{2x^3}\cdot 6x^2}$

Oefening 4

Vind de afgeleide van de volgende samengestelde functie met behulp van de kettingregel:

$f(x)=\sqrt[3]{\text{sen}(x) +x }$

Zie de oplossing

Dit is een samenstelling van functies, omdat we een sinusoïdale functie en een lineaire functie hebben in het argument van een irrationele functie. We berekenen dus eerst de afgeleide van de wortel:

$f(x)=\sqrt[n]{x} \ \longrightarrow \ f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

$f\bigl(g(x)\bigr)=\sqrt[3]{\text{sen}(x) +x } \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }}$

En nu ontlenen we het argument aan de radicaal. Het is een som van functies, dus de afgeleide is de som van de afgeleiden van elke term:

$g(x)=\text{sen}(x) +x \ \longrightarrow \ g'(x)=\cos(x) + 1$

De afgeleide van de gehele functie is dus gelijk aan de vermenigvuldiging van de twee berekende afgeleiden:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f(x)=\sqrt[3]{\text{sen}(x)+x} \ \longrightarrow \ f'(x)& = \cfrac{1}{3\sqrt[3]{\bigl(\text{sen}(x) +x\bigr)^2 }} \cdot \bigl(\cos(x) + 1 \bigr)\\[1.5ex]&=\cfrac{\bm{\cos(x) + 1}}{\bm{3\sqrt[3]{\bigl(\mathbf{sen}(x) +x\bigr)^2} }}\end{aligned}$

Oefening 5

Leid de volgende samenstelling van functies af met behulp van de kettingregel:

$f(x)=3^{x^2+5}$

Zie de oplossing

Om de kettingregel toe te passen, moet je de afgeleide van de macht en de polynoom vinden en deze vervolgens vermenigvuldigen. We leiden dus de kracht af met behulp van de overeenkomstige formule:

$f(x)=a^x \ \longrightarrow \ f'(x)=a^x\cdot \ln (a)$

$f\bigl(g(x)\bigr)=3^{x^2+5} \ \longrightarrow \ f'\bigl(g(x)\bigr)= 3^{x^2+5}\cdot \ln(3)$

Ten tweede leiden we de polynoomfunctie af van de exponent:

$g(x)=x^2+5 \ \longrightarrow \ g'(x)=2x$

En de kettingregel vertelt ons dat de afgeleide van de gehele functie het product is van de afgeleiden die we zojuist hebben gevonden:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$f(x)=3^{x^2+5} \ \longrightarrow \ \bm{f'(x)= 3^{x^2+5}\cdot \ln(3) \cdot 2x}$

Oefening 6

$f(x)=\ln \bigl(4x^2 \cdot \cos(x) \bigr)$

Zie de oplossing

Het is duidelijk dat de functie in dit probleem samengesteld is, aangezien we in het argument van de natuurlijke logaritme een product hebben van twee verschillende soorten functies. Dus differentiëren we eerst de logaritme:

$f(x)=\ln(x) \ \longrightarrow \ f'(x)=\cfrac{1}{x}$

$f\bigl(g(x)\bigr)=\ln \bigl(4x^2 \cdot \cos(x) \bigr) \ \longrightarrow \ f'\bigl(g(x)\bigr)= \cfrac{1}{4x^2 \cdot \cos(x) }$

Ten tweede leiden we de functie af uit het logaritme-argument. Dit is een vermenigvuldiging van twee functies, dus je moet de volgende formule gebruiken om de afleiding te doen:

$z(x)=f(x) \cdot g(x) \ \longrightarrow \ z'(x)=f'(x)\cdot g(x)+f(x) \cdot g'(x)$

$\begin{aligned}g(x)=4x^2 \cdot \cos(x) \ \longrightarrow \ g'(x) & = 8x\cdot \cos(x) + 4x^2 \cdot \bigl(- \text{sen}(x)\bigr) \\[2ex] & = 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x)\end{aligned}$

De afgeleide van de gehele functie zal dus, volgens de kettingregel, het product zijn van de twee afgeleiden:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f'(x)&= \cfrac{1}{4x^2 \cdot \cos(x) } \cdot \bigl( 8x\cdot \cos(x) - 4x^2 \cdot \text{sen}(x) \bigr)\\[1.5ex]&=\cfrac{8x\cdot \cos(x) - 4x^2 \cdot\text{sen}(x)}{4x^2 \cdot \cos(x)}\\[1.5ex]&=\cfrac{\bm{2\cos(x) - x \cdot }\mathbf{sen}\bm{(x)}}{\bm{x \cdot \cos(x) }}\end{aligned}$

Oefening 7

Los de afgeleide van de volgende functie op met behulp van de kettingregel:

$f(x)=\log_9 (e^{x^2}-6x^7)$

Zie de oplossing

Dit is een samenstelling van functies, dus we zullen de logaritme en het bijbehorende argument afzonderlijk differentiëren en vervolgens de afgeleiden vermenigvuldigen.

Dus differentiëren we eerst de logaritme met grondtal 9:

$f(x)=\log_a (x) \ \longrightarrow \ f'(x)=\cfrac{1}{x\cdot \ln (a)}$

$f\bigl(g(x)\bigr)=\log_9 (e^{x^2}-6x^7) \ \longrightarrow \ f'\bigl(g(x)\bigr)=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}$

En nu berekenen we de afgeleide van het argument van de logaritme. Merk op dat het getal e een functie heeft in zijn argument, dat wil zeggen dat het een samengestelde functie is, dus we moeten ook de kettingregel toepassen om deze functie af te leiden:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$h(x)=e^{x^2} \ \longrightarrow \ h'(x)=e^{x^2}\cdot \bigl(x^2\bigr)' =e^{x^2}\cdot 2x$

De afgeleide van het gehele argument van de logaritme zal dus zijn:

$g(x)= e^{x^2}-6x^7\ \longrightarrow \ g'(x)=e^{x^2}\cdot 2x - 42x^6$

En tenslotte zal de afgeleide van de gehele functie het product zijn van f'(g(x)) en g'(x):

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned}f'(x)&=\cfrac{1}{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)} \cdot \bigl(e^{x^2}\cdot 2x - 42x^6\bigr)\\[1.5ex]&=\cfrac{\bm{e^{x^2}\cdot 2x - 42x^6}}{\bm{\bigl(e^{x^2}-6x^7\bigr)\cdot \ln(9)}}\end{aligned}$

Oefening 8

Leid de volgende samengestelde functie af met behulp van de kettingregel:

$f(x)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)$

Zie de oplossing

In deze oefening hebben we een samenstelling van meerdere functies, dus we zullen de kettingregel meerdere keren moeten toepassen. We leiden eerst de trigonometrische functie af van de sinus, waarvan de afgeleide cosinus is:

$f\bigl(g(x)\bigr)=\text{sen}\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)\ \longrightarrow \ f'\bigl(g(x)\bigr)=\cos\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr)$

En nu berekenen we de afgeleide van het sinusargument met behulp van de kettingregel:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\begin{aligned} g(x)= \Bigl( 9x^5 + \cos(x) \Bigr)^2 \cdot g'(x) &= 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(9x^5 + \cos(x) \Bigr)' \\[1.5ex]&=2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-\text{sen}(x)\Bigr)\end{aligned}$

Ten slotte verkrijgen we de afgeleide van de gehele samenstelling van functies door de kettingregel opnieuw toe te passen:

$z(x)=f\bigl(g(x)\bigr) \ \longrightarrow \ z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

$\bm{f'(x)=\cos } \bm{\biggl( \Bigl(9x^5 + \cos(x) \Bigr)^2 \biggr) \cdot 2\Bigl(9x^5 + \cos(x) \Bigr) \cdot \Bigl(45x^4-}\mathbf{sen}\bm{(x)\Bigr)}$

Ketenregelbestendig

Ten slotte zullen we de kettingregelformule bewijzen. Om dit te doen, gaan we uit van de wiskundige definitie van een afgeleide:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Laat z een functie zijn die uit twee functies bestaat:

$z=f\bigl(g(x)\bigr)$

Dan zou de afgeleide van de functie z, waarbij de definitie wordt toegepast, zijn:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}$

Zoals je al weet, kun je een breuk vermenigvuldigen en delen met dezelfde term, omdat dit de uitkomst niet verandert. We kunnen daarom doorgaan naar de volgende stap:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{h}\cdot \frac{g(x+h)-g(x)}{g(x+h)-g(x)}$

We herschikken de noemers van de breuken:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \frac{g(x+h)-g(x)}{h}$

Door de eigenschappen van limieten toe te passen, kunnen we de bovenstaande limiet in tweeën splitsen. Omdat de limiet van een product gelijk is aan het product van de limieten:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f\bigl(g(x+h)\bigr)-f\bigl(g(x)\bigr)}{g(x+h)-g(x)}\cdot \lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

En deze uitdrukking is gelijk aan het volgende:

$\displaystyle z'(x)=f'\bigl(g(x)\bigr)\cdot g'(x)$

De ketenregelformule is dus bewezen, aangezien we hiertoe zijn gekomen vanuit de definitie van de afgeleide.

Ketenregel (derivaten)

Wat is de kettingregel?

Voorbeelden van derivaten met de kettingregel

voorbeeld 1

Voorbeeld 2

Voorbeeld 3

Opgeloste oefeningen over derivaten met de kettingregel

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Oefening 6

Oefening 7

Oefening 8

Ketenregelbestendig

Laat een reactie achter Reactie annuleren