▷ Hoe polynomen te verdelen (opgeloste oefeningen)

Op deze pagina ontdek je hoe je polynomen deelt, zowel de deling van een polynoom door een monomiaal als de deling van een polynoom door een andere polynoom. Je zult ook voorbeelden kunnen zien van het delen van veeltermen en oefenen met stapsgewijze opgeloste oefeningen. En bovendien vindt u de eigenschappen van deze polynomiale bewerking.

Polynomiale (of polynomiale) deling

Voordat we precies zien hoe twee polynomen verdeeld zijn, zullen we kort de concepten van polynomiale deling bespreken, zodat het gemakkelijker zal zijn om de methode die we gaan gebruiken te begrijpen.

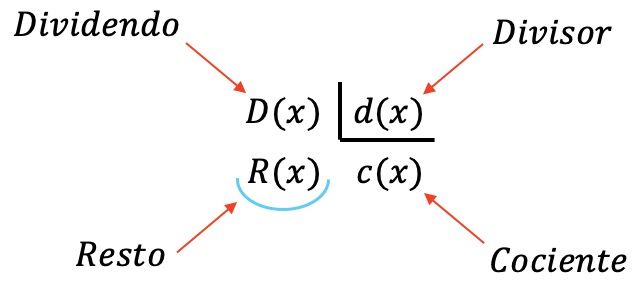
Bij een polynoomverdeling zijn vier polynomen betrokken:

Dividend : het verdeelde polynoom.
Deler : de polynoom die het deeltal deelt.
Quotiënt : resultaat van het delen van het deeltal door de deler.
Rest (of residu): de polynoom die overblijft bij het delen tussen de twee polynomen.

Aan de andere kant moet je ook weten dat er twee soorten verdelingen tussen polynomen zijn:

Exacte verdeling van polynomen : een verdeling tussen polynomen is exact als de rest nul is. In dit geval is het polynoomdividend gelijk aan de deler vermenigvuldigd met het quotiënt.

$D(x)=d(x) \cdot c(x)$

Bovendien, in dit geval, het dividend

$D(x)$

is een veelvoud van de deler

$d(x)$

en het quotiënt

$c(x).$

Op dezelfde manier zijn de polynoomdeler en het polynoomquotiënt beide delers van het deeltal.

Deling van polynomen door gehele getallen : bij een deling van polynomen met gehele getallen (of onnauwkeurig) is de rest niet nul (0). Dan wordt voldaan aan de fundamentele eigenschap van polynomiale deling:

$D(x)=d(x) \cdot c(x) + R(x)$

Nu we hebben gezien wat delende polynomen zijn, gaan we kijken hoe we polynomen door elkaar kunnen delen. Om precies te zijn, zullen we eerst de scheiding tussen een polynoom en een monomiaal uitleggen, en vervolgens de scheiding tussen 2 polynomen.

Deling van een polynoom door een monomiaal

Voordat we zien hoe we een polynoom door een monomiaal kunnen delen, moeten we ons eerst herinneren hoe monomialen onderling worden verdeeld, omdat het nodig is om dit te weten om dit soort polynoombewerkingen uit te kunnen voeren.

Het delen van twee monomialen houdt in dat hun coëfficiënten met elkaar en hun letterlijke delen met elkaar worden gedeeld, dat wil zeggen dat de coëfficiënten van de monomialen worden verdeeld en de exponenten van variabelen met dezelfde basis worden afgetrokken. Kijk naar het volgende voorbeeld:

$12x^5: 3x^2 = \cfrac{12x^5}{3x^2}=(12:3) x^{5-2} = 4x^3$

Laten we nu eens kijken wat de deling van een polynoom door een monomiaal inhoudt:

Om in de wiskunde de deling van een polynoom door een monomiaal op te lossen, wordt elke term van het polynoom gedeeld door het monomiaal.

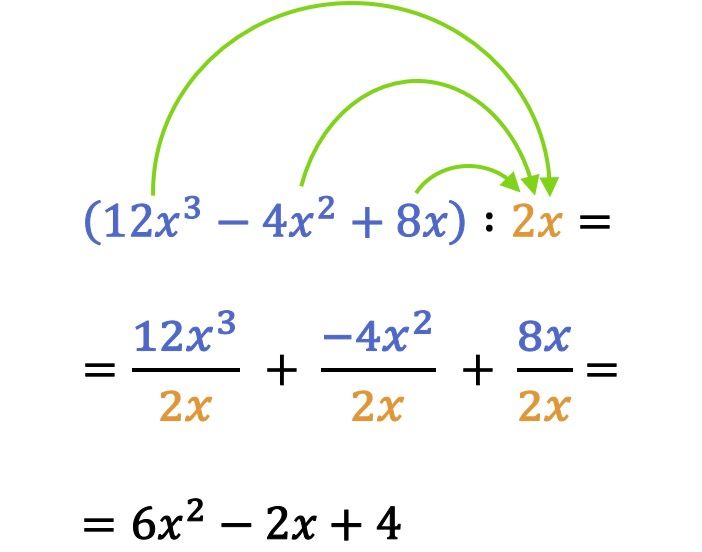
Merk in het vorige voorbeeld van deling op dat je bij het delen van monomialen of polynomen ook rekening moet houden met de tekenregel. Een veel voorkomende fout bij het verdelen van polynomen en monomialen is dat de term verkeerd wordt weergegeven.

Deling van een polynoom door een andere polynoom

Om twee polynomen te delen, moet je een procedure volgen, dus laten we eens kijken hoe de methode voor het delen van polynomen, ook wel staartdeling van polynomen genoemd, eruit ziet door stap voor stap een voorbeeld op te lossen:

Bereken het resultaat van het delen van de polynoom
$P(x)$

tussen de polynoom

$Q(x).$

Zijnde de twee polynomen:

$P(x) =x^3+4x^2+12 \qquad \qquad Q(x) =x-4$

$\cfrac{P(x)}{Q(x)} = \ ?$

Het eerste dat u moet doen, is de polynomen in delingsvorm zetten. Aan de linkerkant schrijven we de teller van de breuk (dividendpolynoom) en aan de rechterkant plaatsen we de noemer van de breuk (delerpolynoom):

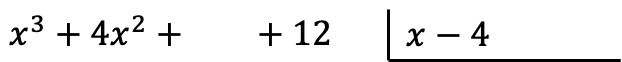
Waarschuwing: als een polynoom geen monomiaal van een bepaalde graad heeft, moeten we een spatie op zijn plaats laten. Bijvoorbeeld de polynoom

$x^3+4x^2+12$

Er is geen eerstejaarstermijn, dus er is een lege ruimte.

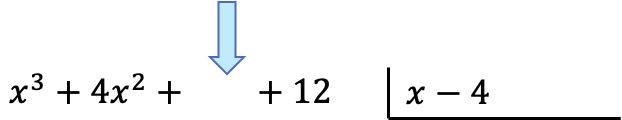
deling van polynomen wanneer een term ontbreekt

Zodra we de polynomen op hun plaats hebben, gaan we het quotiënt vinden. En om de eerste term van het quotiënt te vinden, moeten we de eerste term van het deeltal delen door de eerste term van de deler:

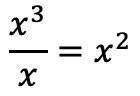
En we plaatsen het resultaat van de deling in plaats van het quotiënt:

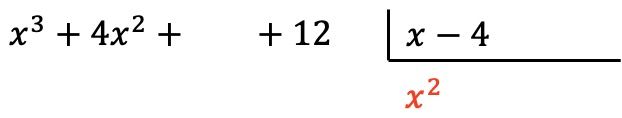
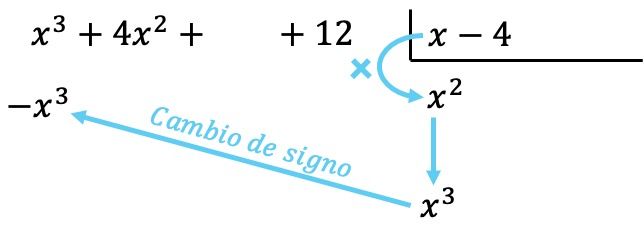
Nu vermenigvuldigen we de term die wordt gevonden door elk element van de deler, en plaatsen we elk resultaat onder het deeltal in de overeenkomstige kolom , waarbij we het teken veranderen :

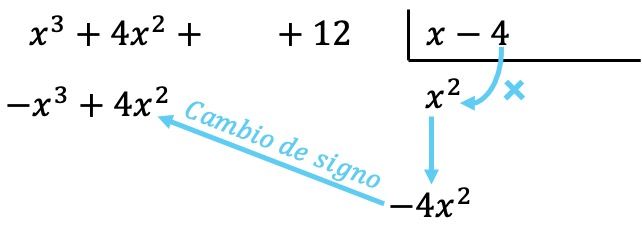
Zoals bij alle bewerkingen met polynomen is het belangrijk om de polynomen van de hoogste graad naar de laagste graad te ordenen, zodat alle termen van dezelfde graad in dezelfde kolom staan.

Zodra we de vermenigvuldigingsresultaten met het tegenovergestelde teken hebben geplaatst, moeten we de verticaal uitgelijnde termen toevoegen:

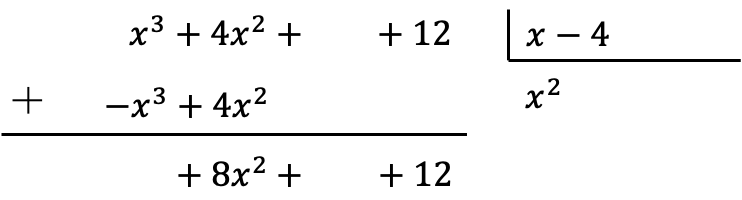
Merk op dat door deze som uit te voeren, de coëfficiënt met de hoogste graad teniet wordt gedaan en dat we daarom één term minder in het dividend hebben.

We moeten nu dezelfde procedure herhalen totdat het polynomiale deeltal één graad minder is dan de polynomiale deler.

We delen daarom de eerste term van het deeltal door de eerste term van de deler:

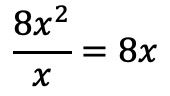
Het resultaat plaatsen we in het quotiënt:

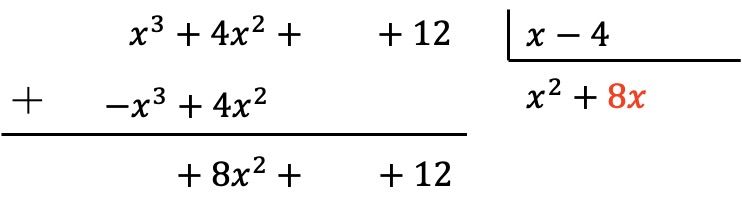
Net als voorheen vermenigvuldigen we de nieuwe term van het quotiënt met elk element van de deler en plaatsen we de resultaten van het tegengestelde teken in de overeenkomstige kolommen van het deeltal:

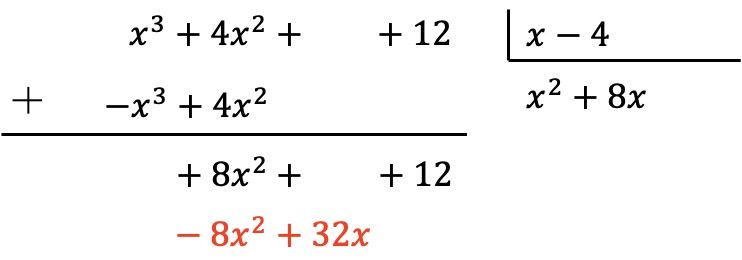
En we voegen verticaal toe:

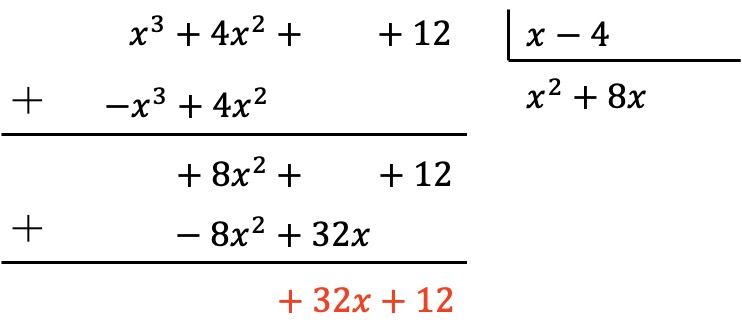
Het dividendpolynoom is nog steeds geen graad minder dan het delerpolynoom, dus we moeten hetzelfde proces blijven volgen.

Dus eerst delen we de eerste term van het deeltal door de eerste term van de deler, dan vermenigvuldigen we het resultaat met elke term van de deler, dan zetten we de gewijzigde resultaten in het teken in het deeltal en tenslotte voegen we verticaal toe:

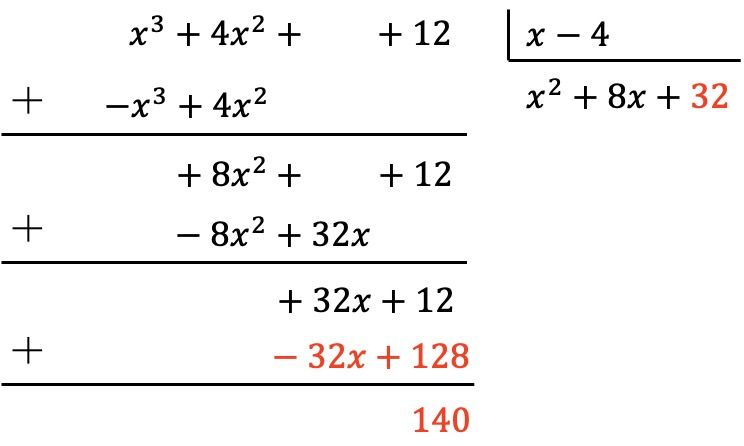
We hebben dus al vastgesteld dat het polynoom van het deeltal een graad kleiner is dan de graad van de deler, omdat het deeltal van graad 0 is en de deler van graad 1. Daarom is de deling voltooid.

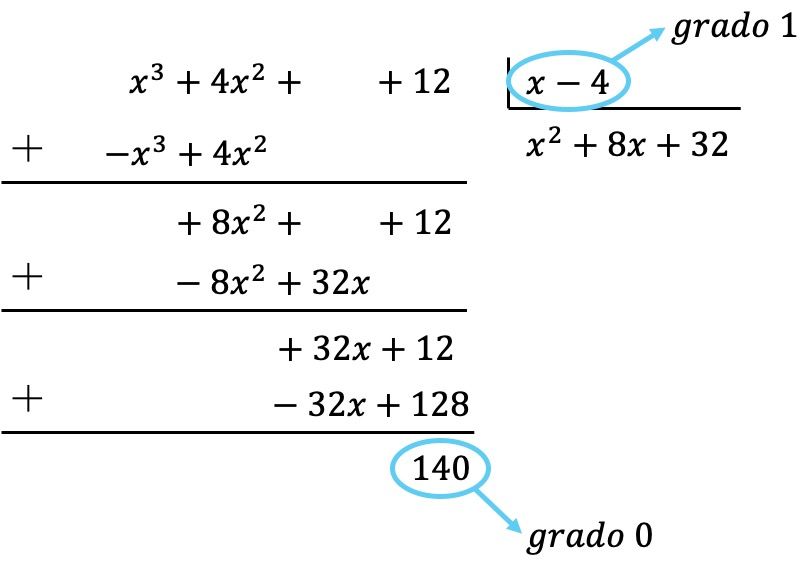
Het resultaat van de deling is dus:

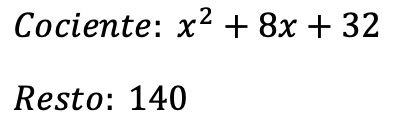
Aan de andere kant kunnen we verifiëren dat we de polynoomdeling correct hebben uitgevoerd op basis van de fundamentele voorwaarde voor de deling van polynomen:

$D(x)=d(x) \cdot c(x) + R(x)$

$x^3+4x^2+12=(x-4) \cdot (x^2+8x+32) + 140$

$x^3+4x^2+12=x^3+8x^2+32x-4x^2-32x-128+ 140$

$x^3+4x^2+12=x^3+4x^2+12$

✅

Er is aan de vergelijking voldaan, dus de polynoomdeling is correct uitgevoerd.

We hopen dat we je met deze uitleg hebben kunnen helpen, zodat we klaar zijn met het delen van veeltermen. Wat vond je van de methode om veeltermen te delen? Heeft u twijfel? Vind je het leuk? Of zou je liever hebben dat polynomiale delingen niet bestonden? 😂 We lezen je in de reacties! 👇👇👇

Eigenschappen van delende polynomen

Elke verdeling van polynomen voldoet aan de volgende kenmerken:

✓ De graad van het polynomiale deeltal moet altijd groter zijn dan de graad van de polynomiale deler.

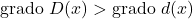$\text{grado } D(x) >\text{grado } d(x)” title=”Rendered by QuickLaTeX.com” height=”19″ width=”193″ style=”vertical-align: -5px;”></p> </p> <p> <strong><span style=$ ✓ De graad van het polynomiale deeltal is gelijk aan de som van de graden van de deler en het quotiënt.

$\text{grado } D(x) =\text{grado } d(x)+\text{grado } c(x)$

✓ De graad van de rest is altijd kleiner dan de graad van de deler (en dus ook van het deeltal).

$\text{grado } R(x) <\text{grado } d(x)$

✓ Het dividend is gelijk aan het product van de deler maal het quotiënt plus de rest. Deze voorwaarde wordt ook gesteld in de deling van getallen.

$D(x)=d(x) \cdot c(x) + R(x)$

Opgeloste oefeningen over de verdeling van veeltermen

Oefening 1

Bepaal het resultaat van de volgende deling van een polynoom door een monomiaal:

$\left(15x^5+9x^3 \right) : \left(3x^2\right)$

Zie de oplossing

Om een polynoom door een monomiaal te delen, moet je de deling van elke term van het polynoom door genoemde monomiaal oplossen:

$\begin{aligned} \left(15x^5+9x^3 \right) : \left(3x^2\right) & = \cfrac{15x^{5}}{3x^2}+ \cfrac{9x^3}{3x^2} \\[2ex] & = \bm{5x^3+3x} \end{aligned}$

Onthoud dat bij het verdelen tussen monomialen de coëfficiënten onder elkaar worden verdeeld en dat de exponenten van machten waarvan de basis hetzelfde is, worden afgetrokken.

Oefening 2

Bereken de volgende deling van een polynoom door een monomiaal:

$\left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right)$

Zie de oplossing

Om een polynoom te delen door een monomiaal, moet je elke term van het polynoom delen door het genoemde monomiaal:

$\begin{aligned} \left( 16x^5-4x^3-20x^2 \right) : \left(4x^2\right) & = \cfrac{16x^5}{4x^2}+ \cfrac{-4x^3}{4x^2} + \cfrac{-20x^2}{4x^2} \\[2ex] & = \bm{4x^3-x-5} \end{aligned}$

Onthoud dat bij monomiale deling de coëfficiënten onder elkaar worden verdeeld en dat de exponenten van machten met een gelijkwaardige basis worden afgetrokken.

Oefening 3

Los de volgende deling van een polynoom door een monomiaal op:

$\left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right)$

Zie de oplossing

Om een polynoom door een monomiaal te delen, moet je de deling van elke term van het polynoom door genoemde monomiaal oplossen:

$\begin{aligned} \left(12x^{10}-30x^7-18x^6+54x^4 \right) : \left(-6x^3\right) & = \cfrac{12x^{10}}{-6x^3}+ \cfrac{-30x^{7}}{-6x^3} + \cfrac{-18x^6}{-6x^3} + \cfrac{54x^4}{-6x^3} \\[2ex] & = \bm{-2x^7+5x^4+3x^3-9x} \end{aligned}$

Houd er rekening mee dat de verdelende monomiaal negatief is en dat daarom de tekenen van alle verdeeldheid veranderen.

Oefening 4

Voer de volgende verdeling van de polynomen uit:

$\cfrac{x^4+x^3-x^2+x+1}{x^3-5}$

Zie de oplossing

Om polynomen te delen, moet u de hierboven uitgelegde methode toepassen:

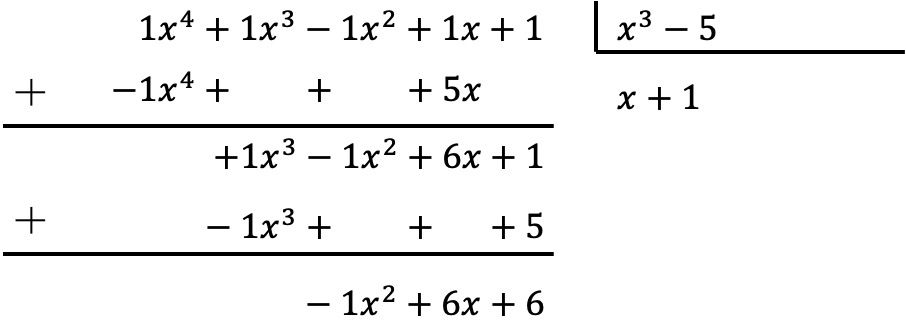
Het resultaat van de deling tussen de twee polynomen is daarom:

Quotiënt:

$x+1$

Rest:

$-x^2+6x+6$

Oefening 5

Bereken de volgende verdeling van polynomen:

$\cfrac{2x^3-3x^2-5x-5}{x-2}$

Zie de oplossing

Om de deling van de polynoom door de binominale op te lossen, moeten we de methode toepassen die we hierboven zagen:

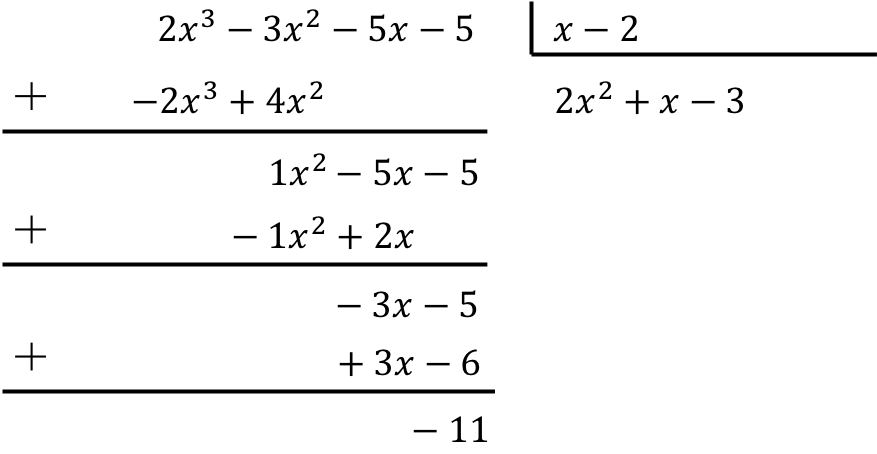
oefeningen die stap voor stap worden opgelost voor de deling van polynomen

Het resultaat van de polynomiale deling is daarom:

Quotiënt:

$2x^2+x-3$

Rest:

$-11$

Oefening 6

Los de volgende verdeling van polynomen op:

$\cfrac{x^4+x^2+3}{x^3+3x^2+2x}$

Zie de oplossing

Om de verdeling van polynomen te berekenen, moeten we de uitgelegde methode toepassen:

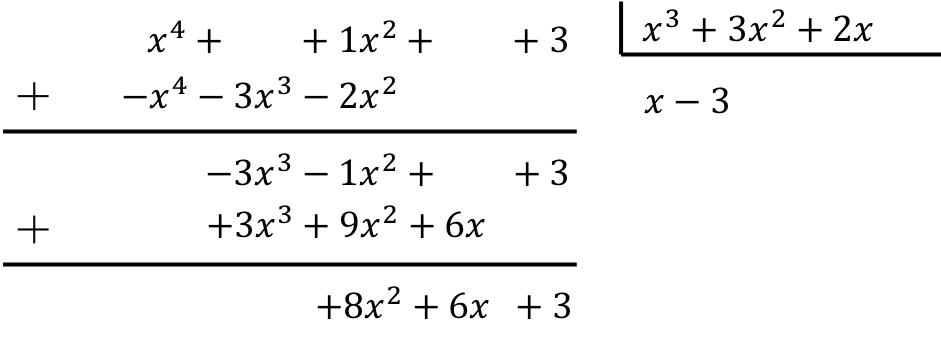
voorbeeld van een deling van 2 polynomen

Het resultaat van de deling tussen de twee polynomen is daarom:

Quotiënt:

$x-3$

Rest:

$8x^2+6x+3$

Oefening 7

Zoek het resultaat van de volgende verdeling tussen 2 polynomen:

$\cfrac{x^4-2x^3+x^2-x-3}{x^2+x+1}$

Zie de oplossing

Om de deling van de polynoom door de trinominaal te berekenen, moet je de uitgelegde methode toepassen:

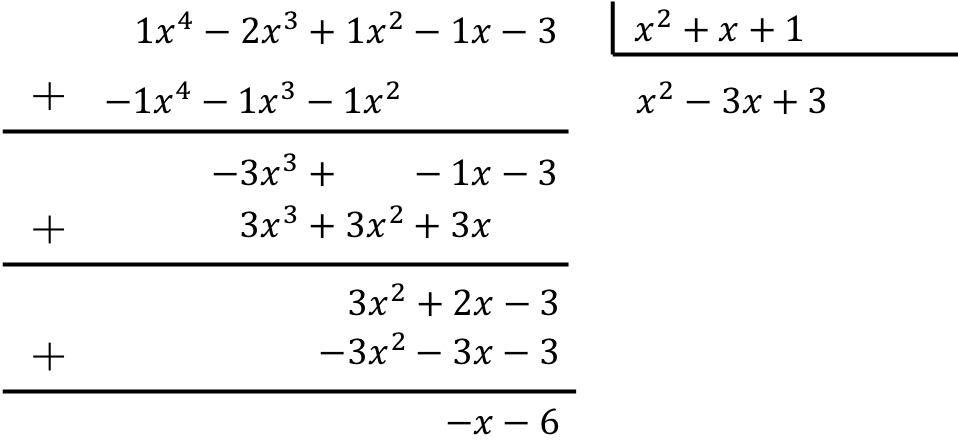
oefeningen stap voor stap opgelost om veeltermen te delen

Het resultaat van de deling tussen de twee polynomen is daarom:

Quotiënt:

$x^2-3x+3$

Rest:

$-x-6$

👉👉👉Als je zo ver bent gekomen, betekent dit dat je al weet hoe veeltermen worden verdeeld. Helder! Nu je het delen van veeltermen onder de knie hebt, weet je dat er een methode is waarmee je bepaalde delingen tussen veeltermen veel sneller kunt oplossen . Dit is een synthetische divisie of Ruffini-regel , je kunt zien hoe deze truc wordt toegepast en wanneer deze kan worden gebruikt door op de link te klikken.😉

Polynomiale deling

Polynomiale (of polynomiale) deling

Deling van een polynoom door een monomiaal

Deling van een polynoom door een andere polynoom

Eigenschappen van delende polynomen

Opgeloste oefeningen over de verdeling van veeltermen

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Oefening 6

Oefening 7

Laat een reactie achter Reactie annuleren