Vermenigvuldiging (of product) van polynomen

Op deze pagina leer je hoe polynomen worden vermenigvuldigd. Je zult ook voorbeelden zien van vermenigvuldiging van polynomen en bovendien oefeningen die stap voor stap worden opgelost. Ten slotte ontdek je wat de eigenschappen van vermenigvuldigende veeltermen zijn.

Om het concept van het vermenigvuldigen van polynomen echter volledig te begrijpen, gaan we van de meest elementaire naar de meest gecompliceerde, dat wil zeggen, we beginnen met hoe we een polynoom met een getal kunnen vermenigvuldigen, en dan zullen we zien hoe we een polynoom met een getal kunnen vermenigvuldigen. een monomial en ten slotte zullen we uitleggen hoe je twee of meer polynomen met elkaar kunt vermenigvuldigen.

Ik raad je aan deze volgorde aan te houden, maar als je denkt dat je de bewerkingen met de voorgaande polynomen al onder de knie hebt, kun je direct naar de vermenigvuldiging tussen polynomen gaan door op de index te klikken:

Vermenigvuldig een polynoom met een getal

Het product van een scalair (of een getal) en een polynoom is vrij eenvoudig op te lossen; vermenigvuldig gewoon het getal met de coëfficiënt van elke term van de polynoom .

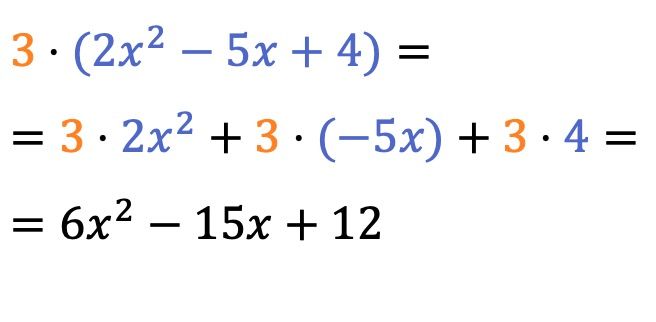
Het vermenigvuldigingsteken vóór de haakjes kan worden weggelaten.

Een polynoom vermenigvuldigen met een monomiaal

Voordat we gaan zien hoe we een polynoom met een monomiaal kunnen vermenigvuldigen, zullen we ons eerst herinneren hoe monomialen zich met elkaar vermenigvuldigen, omdat je dit moet weten om dit soort polynoombewerkingen uit te kunnen voeren.

Het product van twee monomialen bestaat uit het vermenigvuldigen van hun coëfficiënten met elkaar en hun letterlijke delen met elkaar, dat wil zeggen dat de coëfficiënten van de monomialen worden vermenigvuldigd en de exponenten van de variabelen met dezelfde basis worden opgeteld. Kijk naar het volgende voorbeeld:

Laten we nu eens kijken hoe we een monomiaal met een polynoom kunnen vermenigvuldigen:

Om in de wiskunde de vermenigvuldiging van een monomiaal met een polynoom op te lossen, wordt het monomiaal vermenigvuldigd met elke term in het polynoom.

Net als voorheen kan het vermenigvuldigingsteken ook worden weggelaten:

Merk in het vorige voorbeeld op dat je bij het vermenigvuldigen van monomialen of polynomen ook rekening moet houden met de tekenregel. Een veel voorkomende fout bij het vermenigvuldigen van monomialen en polynomen is dat je merkt dat een term verkeerd is.

Toen je op een gegeven moment iets nieuws in de wiskunde zag, vroeg je je vast af: waar is het voor ? Welnu, dit type vermenigvuldiging wordt gebruikt om de gemeenschappelijke factor van een polynoom te verkrijgen, een bewerking waarmee je polynomen kunt vereenvoudigen (erg handig). In deze link kunt u zien wat het is en hoe de gemeenschappelijke factor van een polynoom wordt berekend.

Vermenigvuldiging van twee veeltermen

Als we eenmaal weten hoe we polynomen met getallen en met monomialen moeten vermenigvuldigen, gaan we kijken wat het is en hoe we polynomen met polynomen kunnen vermenigvuldigen.

Om precies te zien wat deze methode is, lossen we stap voor stap de volgende vermenigvuldiging van polynomen op:

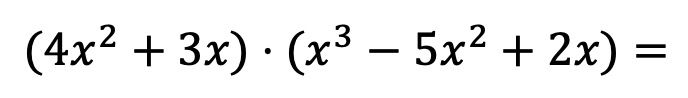
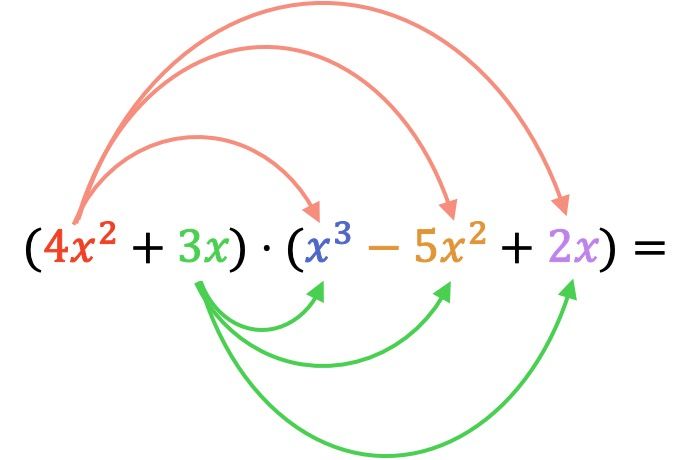
Allereerst moeten we elk element van het eerste vermenigvuldigingspolynoom vermenigvuldigen met elke term van het tweede polynoom:

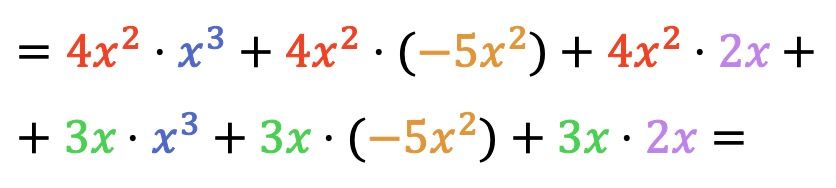
Nu doen we alle vermenigvuldigingen van monomials:

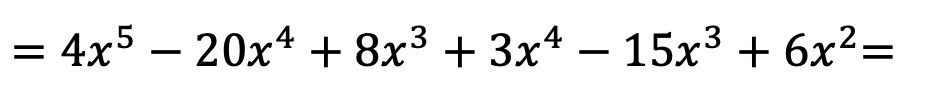
Nadat we de polynomen met elkaar hebben vermenigvuldigd, hoeven we alleen maar de resulterende termen te groeperen die vergelijkbaar zijn, dat wil zeggen de termen met dezelfde letter en dezelfde exponent:

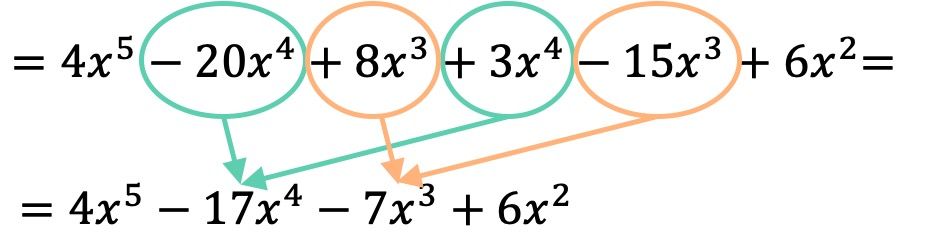
Het resultaat van de polynomiale vermenigvuldiging is daarom:

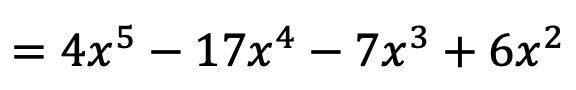
En op deze manier hebben we de vermenigvuldiging van polynomen al berekend. Misschien lijkt het je nu heel moeilijk, maar je zult zien dat als je met twee of drie oefeningen oefent, het veel gemakkelijker gaat.

Nu je hebt gezien hoe de vermenigvuldiging tussen twee polynomen wordt opgelost, wil je waarschijnlijk weten hoe je polynomen moet verdelen . In feite is het delen van veeltermen veel ingewikkelder dan het vermenigvuldigen ervan. Daarom hebben we de procedure (en tips😉) stap voor stap uitgelegd, zodat u deze volledig kunt begrijpen. Als je geïnteresseerd bent, klik dan op deze link om te zien hoe polynomen worden verdeeld.

Verticale polynomiale vermenigvuldiging

We hebben zojuist gezien hoe je een polynoom horizontaal kunt vermenigvuldigen met een andere polynoom, maar dit kan ook op een meer klassieke manier: vermenigvuldig polynomen verticaal. Laten we eens kijken hoe deze methode wordt gebruikt door een voorbeeld van polynomiale vermenigvuldiging op te lossen.

Als we de volgende twee polynomen verticaal willen vermenigvuldigen:

Het eerste dat we moeten doen is de ene polynoom onder de andere plaatsen, als een algebraïsche vermenigvuldiging van polynomen:

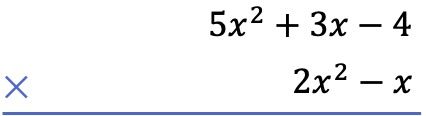
Ten tweede vermenigvuldigen we elke term van de onderstaande polynoom met elke term van de bovenstaande polynoom, en plaatsen we de resultaten gerangschikt in kolommen van de hoogste graad naar de laagste graad:

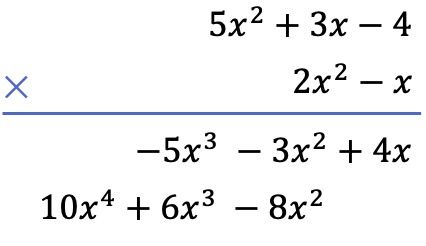
En tot slot voegen we de verticaal uitgelijnde termen toe:

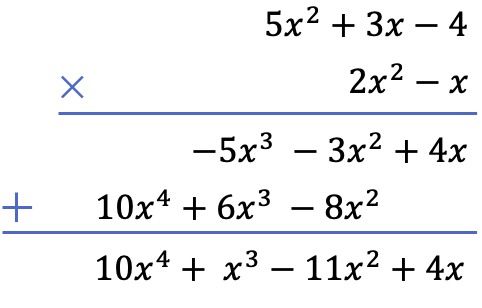
Nu je de twee methoden hebt gezien die er bestaan om een vermenigvuldiging van veeltermen op te lossen, wist je dan dat je ook breuken met veeltermen kunt vermenigvuldigen ? En niet alleen vermenigvuldigingen, maar met dit soort breuken kunnen allerlei bewerkingen worden uitgevoerd. Klik op deze link en ontdek wat algebraïsche breuken zijn.

Eigenschappen van polynomiale vermenigvuldiging

De vermenigvuldiging van polynomen heeft de volgende kenmerken:

• Commutatieve eigenschap : de volgorde van de vermenigvuldigingspolynomen verandert het resultaat van de vermenigvuldiging niet.

• Associatieve eigenschap : Wanneer drie of meer polynomen worden vermenigvuldigd, is het productresultaat hetzelfde, ongeacht hoe de factoren zijn gegroepeerd:

• Distributieve eigenschap : de som van twee polynomen vermenigvuldigd met een derde is gelijk aan de som van elke optelling vermenigvuldigd met de derde polynoom.

• De graad van de polynoom die voortkomt uit een vermenigvuldiging tussen twee polynomen is gelijk aan de som van de graden van de twee vermenigvuldigde polynomen.

Opgeloste oefeningen over vermenigvuldiging van polynomen

Zodat je kunt oefenen, laat ik je een aantal opgeloste oefeningen over de vermenigvuldiging van polynomen achter. U kunt proberen ze zelf op te lossen en uw resultaten controleren met de voorgestelde oplossing. Je kunt ons dan al je vragen stellen in de reacties, we helpen je graag verder.

Oefening 1

Bereken de volgende producten tussen polynomen en scalairen:

Om de vermenigvuldiging van een polynoom met een getal te berekenen, moet u het getal vermenigvuldigen met de coëfficiënt van elk element van de polynoom. DUS:

Oefening 2

Los de volgende vermenigvuldigingen op tussen polynomen en monomialen:

Om de vermenigvuldiging van een polynoom met een monomiaal op te lossen, moet je het genoemde monomiaal vermenigvuldigen met elke term van het polynoom. DUS:

Oefening 3

Bepaal het resultaat van de volgende vermenigvuldigingen tussen polynomen:

Om een vermenigvuldiging van twee polynomen te berekenen, moeten we elk element van de eerste polynoom vermenigvuldigen met elk element van de tweede polynoom en vervolgens soortgelijke termen samenvoegen. DUS:

Oefening 4

Zoek het resultaat van de volgende vermenigvuldigingen tussen polynomen:

Om een vermenigvuldiging van twee polynomen te berekenen, moeten we elk element van de eerste polynoom vermenigvuldigen met elk element van de tweede polynoom, en vervolgens de soortgelijke termen toevoegen. DUS:

Oefening 5

Bereken de volgende vermenigvuldigingen van polynomen:

Om een product van 2 polynomen te maken, moet je elke term van de eerste polynoom vermenigvuldigen met elke term van de tweede polynoom, en vervolgens de verkregen soortgelijke monomialen groeperen. Nog:

Oefening 6

Los de volgende vermenigvuldiging van 3 polynomen op:

De werking van het probleem bestaat uit 2 vermenigvuldigingen van polynomen, meer bepaald uit twee binomialen en een trinominaal. We moeten dus eerst een product oplossen en vervolgens het resultaat vermenigvuldigen met de resterende polynoom.

We berekenen daarom de eerste vermenigvuldiging:

En nu lossen we de resterende vermenigvuldiging op:

Oefening 7

Vermenigvuldig de volgende polynomen met rationale coëfficiënten (met breuken):

Hoewel polynomen breuken hebben, is het nog steeds een vermenigvuldiging tussen twee polynomen. Het moet daarom worden opgelost zoals elk polynoomproduct: vermenigvuldig alle elementen met elkaar en groepeer vervolgens vergelijkbare monomialen.

We vermenigvuldigen daarom de polynomen:

En ten slotte voegen we de termen toe (of trekken ze af) waarvan de letterlijke delen identiek zijn:

Om deze oefening succesvol af te ronden, was het belangrijk dat je de bewerkingen met breuken beheerst. Maar als u vragen heeft over een bepaalde stap, kunt u deze stellen in de opmerkingen en wij zullen deze zo snel mogelijk beantwoorden.