Operaties met monomials

Op deze pagina leggen we uit hoe je alle bewerkingen met monomialen uitvoert (optellen, aftrekken, vermenigvuldigen, delen en macht). Bovendien kunt u voorbeelden zien van elk type operatie met monomials en oefenen met oefeningen die stap voor stap worden opgelost.

Optellen en aftrekken van monomials

Twee of meer monomialen kunnen alleen worden opgeteld of afgetrokken als het vergelijkbare monomialen zijn, dat wil zeggen als de twee monomialen een identiek letterlijk deel hebben (dezelfde letters en dezelfde exponenten).

Vervolgens is de som (of aftrekking) van twee soortgelijke monomialen gelijk aan een andere monomial die bestaat uit hetzelfde letterlijke deel en de som (of aftrekking) van de coëfficiënten van deze twee monomialen.

Optellen en aftrekken van monomials worden ook respectievelijk optellen en aftrekken van monomials genoemd.

Voorbeelden van optellen en aftrekken van monomials

Zodat u duidelijk begrijpt hoe u twee of meer monomialen moet optellen en aftrekken, laten we hieronder enkele voorbeelden achter:

• 

• 

• 

• 

• 

De monomialen in het laatste voorbeeld kunnen niet worden opgeteld of afgetrokken omdat ze niet vergelijkbaar zijn of, met andere woorden, verschillende onbekenden of exponenten hebben.

Product van een aantal maal een monomial

Om het product van een monomiaal met een getal op te lossen, vermenigvuldigt u eenvoudigweg de coëfficiënt van het monomial met dat getal, waarbij het letterlijke deel van het monomial hetzelfde blijft.

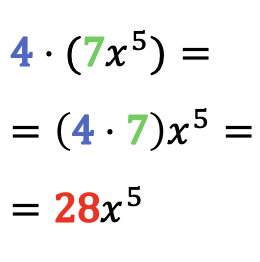
Voorbeelden van het vermenigvuldigen van getallen met monomials

• 

• 

• 

• 

Vermenigvuldiging van monomialen

Het resultaat van de vermenigvuldiging van twee monomialen is een andere monomial waarvan de coëfficiënt het product is van de coëfficiënten van de monomialen en waarvan het letterlijke deel wordt verkregen door de variabelen die dezelfde basis hebben te vermenigvuldigen, dat wil zeggen door hun exponenten op te tellen.

Om twee verschillende monomialen te vermenigvuldigen, moeten we daarom de coëfficiënten daartussen vermenigvuldigen en de exponenten van de machten met dezelfde basis optellen.

Als we echter twee monomialen met verschillende basismachten vermenigvuldigen , hoeven we alleen maar hun coëfficiënten met elkaar te vermenigvuldigen en de machten hetzelfde te laten. Bijvoorbeeld:

Aan de andere kant moet bij het vermenigvuldigen van monomialen rekening worden gehouden met de tekenregel:

• Een positieve monomial vermenigvuldigd met een positieve monomial levert nog een positieve monomial op.
• Een positieve monomial vermenigvuldigd met een negatieve monomial (of omgekeerd) is gelijk aan een negatieve monomial.
• Twee negatieve monomialen met elkaar vermenigvuldigd geven aanleiding tot een positieve monomial.

Voorbeelden van monomiale vermenigvuldigingen

Hieronder staan verschillende voorbeelden van vermenigvuldiging tussen monomialen, zodat je kunt zien hoe het werkt:

• 

• 

• 

• 

• 

Zoals je hebt gezien, is het oplossen van een vermenigvuldiging van monomialen relatief eenvoudig. Maar u moet er rekening mee houden dat monomialen ook met polynomen kunnen worden vermenigvuldigd, en dat zelfs twee of meer polynomen met elkaar kunnen worden vermenigvuldigd. Als u meer geïnteresseerd bent, kunt u zien hoe al deze bewerkingen werken door op polynomiale vermenigvuldiging te klikken.

Verdeling van monomialen

In de wiskunde is het resultaat van de deling van monomialen een andere monomial waarvan de coëfficiënt gelijk is aan het quotiënt van de coëfficiënten van de monomialen en waarvan het letterlijke deel wordt verkregen door de variabelen te delen die dezelfde basis hebben, dat wil zeggen door hun exponenten af te trekken. .

Uiteraard kan elke verdeling van monomialen ook als een breuk worden uitgedrukt:

Net als bij vermenigvuldiging is het bij de verdeling van monomialen noodzakelijk om de wet van tekens toe te passen:

• Een positieve monomial gedeeld door een positieve monomial geeft nog een positieve monomial.
• Een positieve monomial gedeeld door een negatieve monomial (of omgekeerd) is gelijk aan een negatieve monomial.
• Twee negatieve monomialen die door elkaar worden gedeeld, geven aanleiding tot een positieve monomial.

Voorbeelden van de verdeling van monomials

Hieronder kunt u meer voorbeelden zien van hoe twee of meer monomialen zijn verdeeld:

• 

• 

• 

• 

• 

Toen je op een gegeven moment iets nieuws leerde in de wiskunde, vroeg je je vast af: waar is het voor ? Welnu, monomiale deling wordt gebruikt om polynomen te verdelen. Het is zelfs heel gebruikelijk dat er een fout wordt gemaakt bij het delen van polynomen, omdat twee monomialen verkeerd zijn verdeeld. Daarom raden we aan dat je, nu je bekend bent met de deling tussen monomialen, ziet hoe de deling van polynomen wordt berekend, omdat het nu veel gemakkelijker voor je zal zijn om de procedure te leren (het is behoorlijk ingewikkeld).

De kracht van een monomial

Om de macht van een monomial te berekenen, wordt in de wiskunde elk element van de monomial verheven tot de exponent van de macht . Met andere woorden, de macht van een monomial bestaat uit het verhogen van de coëfficiënt en de variabelen (letters) ervan tot de exponent van de macht.

Onthoud uit de eigenschappen van machten dat wanneer beide een toch al hoge term verhogen, exponenten zich vermenigvuldigen. Dit is de reden waarom , tot de macht van een monomial, de exponent van elke letter altijd wordt vermenigvuldigd met de exponent die de macht aangeeft .

Aan de andere kant, om deze operatie correct uit te voeren, moet u de volgende eigenschap van bevoegdheden onthouden:

• Een negatieve monomial verhoogd tot een even exponent is gelijk aan een positieve monomial.
• In plaats daarvan resulteert een negatieve monomial verhoogd tot een oneven exponent in een negatieve monomial.

Voorbeelden van bevoegdheden van monomials

We laten u enkele voorbeelden achter, zodat u duidelijk kunt begrijpen hoe de kracht van een monomial wordt berekend:

• 

• 

• 

• 

• 

Operaties gecombineerd met monomials

Als je eenmaal hebt gezien wat alle bewerkingen met monomials zijn, weet dan dat ze ook met elkaar kunnen worden gecombineerd. Dat wil zeggen dat we oefeningen kunnen vinden waarin ons wordt gevraagd bewerkingen met monomialen op te lossen waarbij alle typen betrokken zijn: optellen, aftrekken, vermenigvuldigen, delen en machten.

Maar maak je geen zorgen, ze zijn niet zo moeilijk als ze lijken. Het enige dat u hoeft te onthouden, is de volgorde waarin de gecombineerde bewerkingen worden opgelost:

1. Ten eerste worden bewerkingen met monomialen tussen haakjes opgelost.
2. Vervolgens worden de krachten van de monomialen berekend.
3. Ten derde worden vermenigvuldigingen en delingen van monomialen uitgevoerd.
4. En ten slotte worden de optellingen en aftrekkingen van monomialen bepaald.

Ik ben er zeker van dat je door het oplossen van een voorbeeld het duidelijker zult zien:

Voorbeeld van gecombineerde werking van monomials

Allereerst moeten we de bewerkingen met monomialen tussen haakjes oplossen:

In dit geval hebben wij geen macht. Laten we nu de vermenigvuldigingen en delingen van monomialen berekenen:

En ten slotte tellen we monomialen op en af:

Opgeloste oefeningen over operaties met monomials

Als u wilt oefenen, laten we u hieronder verschillende oefeningen zien die stap voor stap zijn opgelost met de ESO-moeilijkheidsgraad bij operaties met monomials.

Oefening 1

Bereken de volgende optellingen en aftrekkingen van monomials:

Oefening 2

Los de volgende vermenigvuldigingen van monomialen op: