▷ Concaviteit en convexiteit van een functie (kromming)

Hier leert u wat concaafheid en convexiteit van een functie zijn en hoe u kunt bepalen of een functie concaaf of convex is. Daarnaast kun je oefenen met stapsgewijze oefeningen op de kromming van een functie.

Wat is de concaviteit en convexiteit van een functie?

Concaviteit en convexiteit van een functie verwijzen naar de kromming van de grafiek van een functie. Een concave functie is een functie waarvan de grafiek de vorm heeft van een berg, en een convexe functie is een functie waarvan de grafiek de vorm heeft van een vallei.

In de vorige paragraaf zijn concave en convexe functies informeel gedefinieerd voor het gemak van begrip, maar de wiskundige definitie van concave functie en convexe functie is als volgt:

Concave functie: wanneer het segment dat twee willekeurige punten van de functie verbindt, zich onder de curve bevindt.
Convexe functie: wanneer het segment dat twee willekeurige punten van de functie verbindt, zich boven de curve bevindt.

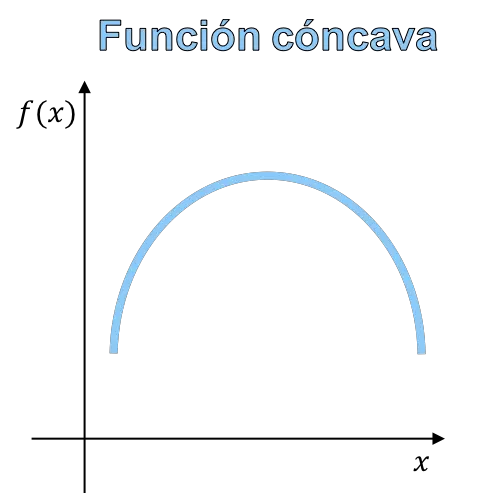
Uiteindelijk ligt het verschil tussen een concave functie en een convexe functie in de vorm van de functie en daarom kun je concaviteit van convexiteit onderscheiden in de grafiek van de functie.

Een functie hoeft echter niet noodzakelijkerwijs concaaf of convex te zijn over het gehele domein, maar kan ook concaaf zijn over het ene interval en convex over een ander interval.

Opmerking: de wiskundige gemeenschap is het er nog steeds niet helemaal mee eens en daarom zeggen sommige professoren het tegenovergestelde: ze noemen een functie concaaf en heeft de vorm van een

$\bm{\cup}$

, en een convexe functie die de vorm heeft van

$\bm{\cap}$

. Het belangrijkste is in ieder geval om te weten wat de functie is, wat de naam ook is.

Hoe de kromming van een functie te bestuderen

Het bestuderen van de kromming van een functie omvat het vinden van de concaafheid en convexiteit van de functie, dat wil zeggen het kennen van de intervallen waarin de functie concaaf is en de intervallen waarin de functie convex is.

Om de kromming van een functie te bestuderen, moeten dus de volgende stappen worden uitgevoerd:

Zoek de punten die niet tot het domein van de functie behoren .
Bereken de eerste afgeleide en tweede afgeleide van de functie.
Vind de wortels van de tweede afgeleide , dat wil zeggen, bereken de punten die de tweede afgeleide opheffen door op te lossen
$f''(x)=0$

.
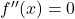
Maak intervallen met de wortels van de afgeleide en de punten die niet tot het domein van de functie behoren.
Bereken de waarde van de tweede afgeleide op een punt in elk interval.
Het teken van de tweede afgeleide bepaalt dus de concaafheid of convexiteit van de functie in dit interval:
- Als de tweede afgeleide van de functie positief is, is de functie convex op dit interval.
- Als de tweede afgeleide van de functie negatief is, is de functie op dit interval concaaf .

Voorbeeld van hoe u de kromming van een functie kunt vinden

Vervolgens zullen we stap voor stap een voorbeeld oplossen, zodat u kunt zien hoe de concaafheid en convexiteitsintervallen van een functie worden berekend.

Bestudeer de concaafheid en convexiteit van de volgende functie:

$f(x)=x^3-3x$

Het eerste dat u moet doen, is het domein van de definitie van de functie berekenen. In dit geval hebben we een polynomiale functie, dus het domein van de functie bestaat uit reële getallen:

$\text{Dom } f= \mathbb{R}$

Nadat we het domein van de functie hebben berekend, moeten we onderzoeken op welke punten de tweede afgeleide van de functie verdwijnt.

We berekenen daarom de eerste afgeleide van de functie:

$f(x)=x^3-3x \ \longrightarrow \ f'(x)= 3x^2-3$

We vinden dan de tweede afgeleide van de functie:

$f'(x)=3x^2-3 \ \longrightarrow \ f''(x)= 6x$

En nu stellen we de tweede afgeleide gelijk aan 0 en lossen we de vergelijking op:

$f''(x)=0$

$6x=0$

$x=\cfrac{0}{6}$

$x=0$

Zodra we het domein van de functie en hebben berekend

$f''(x)=0$

, vertegenwoordigen we alle kritieke punten op de lijn. In dit geval hebben we geen enkel kritisch punt gevonden in de berekening van het definitiedomein van de functie, maar hebben we een punt verkregen dat de tweede afgeleide van de functie annuleert:

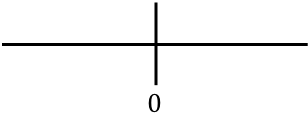
En nu evalueren we het teken van de tweede afgeleide in elk interval, om te weten of de functie concaaf of convex is. We nemen daarom in elk interval een punt (nooit de kritische punten) en kijken welk teken de tweede afgeleide op dit punt heeft:

$f''(x)=6x$

$f''(-1) = 6\cdot (-1)=-6 \ \rightarrow \ \bm{-}$

$f''(1) = 6\cdot 1=+6 \ \rightarrow \ \bm{+}$

Ten slotte leiden we de concaafheid en convexiteitsintervallen van de functie af. Als de tweede afgeleide positief is, betekent dit dat de functie convex is.

$(\bm{\cup})$

, en als de tweede afgeleide negatief is, betekent dit dat de functie concaaf is

$(\bm{\cap})$

. De concaafheid en convexiteitsintervallen van de functie zijn dus:

Convex

$(\bm{\cup})$

$\bm{(0,+\infty)}$

Concaaf

$(\bm{\cap})$

$\bm{(-\infty,0)}$

Opgeloste oefeningen over de concaviteit en convexiteit van een functie

Oefening 1

Bereken de concaafheid en convexiteitsintervallen van de volgende polynoomfunctie:

$f(x) = x^3-3x^2-2x$

Zie de oplossing

De functie in de oefening is een polynoom, dus het domein van de functie bestaat uit reële getallen:

$\text{Dom } f= \mathbb{R}$

Nadat we het domein van de functie hebben bepaald, differentiëren we deze:

$f(x)=x^3-3x^2-2x \ \longrightarrow \ f'(x)= 3x^2-6x-2$

We vinden dan de tweede afgeleide van de functie:

$f'(x)= 3x^2-6x-2 \ \longrightarrow \ f''(x)= 6x-6$

En nu stellen we de tweede afgeleide gelijk aan 0 en lossen we de vergelijking op:

$f''(x)= 0$

$6x-6= 0$

$6x= 6$

$x= \cfrac{6}{6}$

$x=1$

Zodra we het domein van de functie hebben berekend en opgelost

$f''(x)=0$

vertegenwoordigen we alle singuliere punten op de getallenlijn:

En laten we nu een punt nemen dat bij elk interval hoort en kijken welk teken op dit punt de tweede afgeleide heeft:

$f''(0)= 6\cdot 0-6 = -6 \ \rightarrow \ \bm{-}$

$f''(2)= 6\cdot 2-6 = 12-6=+6 \ \rightarrow \ \bm{+}$

Wanneer de tweede afgeleide groter is dan nul, betekent dit dat de functie convex is.

$(\bm{\cup})$

, maar als de tweede afgeleide negatief is, impliceert dit dat de functie concaaf is

$(\bm{\cap})$

. Daarom zijn de concaafheids- en convexiteitsintervallen:

Convex

$(\bm{\cup})$

$\bm{(1,+\infty)}$

Concaaf

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Oefening 2

Bestudeer de kromming van de volgende rationale functie:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Zie de oplossing

Eerst moeten we het domein van de functie berekenen. Omdat dit een rationale functie is, stellen we de noemer gelijk aan nul om te zien welke getallen niet tot het domein van de functie behoren:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Dit betekent dat wanneer x -2 of +2 is, de noemer 0 zal zijn. En daarom zal de functie niet bestaan. Het domein van de functie bestaat dus uit alle getallen behalve x=-2 en x=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

Ten tweede berekenen we de eerste afgeleide van de functie:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

En dan lossen we de tweede afgeleide op:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Alle termen worden vermenigvuldigd met

$(x^2-4)$

. We kunnen de breuk daarom vereenvoudigen:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Laten we nu de wortels van de tweede afgeleide van de functie berekenen:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

De voorwaarde

$\left(x^2-4\right)^3$

Dit houdt in dat we de hele linkerkant delen, zodat we deze met de hele rechterkant kunnen vermenigvuldigen:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

We halen de gemeenschappelijke factor eruit:

$x(8x^2+96)=0$

Om de vermenigvuldiging gelijk te maken aan 0, moet een van de twee elementen van de vermenigvuldiging nul zijn. Daarom stellen we elke factor gelijk aan 0:

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Er is geen oplossing omdat er geen negatieve wortel is van een reëel getal.

We geven nu op de lijn alle verkregen kritische punten weer, dat wil zeggen de punten die niet tot het domein behoren (x=-2 en x=+2) en die welke de tweede afgeleide opheffen (x=0):

En we evalueren het teken van de tweede afgeleide in elk interval, om te weten of de functie concaaf of convex is. We nemen dus een punt in elk interval en kijken welk teken op dat punt de tweede afgeleide heeft:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Als de tweede afgeleide positief is, betekent dit dat de functie convex is.

$(\bm{\cup})$

, en als de tweede afgeleide negatief is, betekent dit dat de functie concaaf is

$(\bm{\cap})$

. De concaviteits- en convexiteitsintervallen zijn daarom:

Convex

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

Concaaf

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

Oefening 3

Een functie

$f(x)$

heeft een relatief extreem in

$x=3$

. En bovendien is de functie convex

$(\cup )$

op ditzelfde punt. Bepaal of het relatieve uiterste een minimum of een maximum is.

➤ Zie: definitie van maxima en minima van een functie

Zie de oplossing

Laat de convexe functie

$(\cup)$

$x=3$

betekent dat de tweede afgeleide op dit punt positief is, dwz

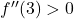$f''(3)>0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”74″ style=”vertical-align: -5px;”></p> <p> .</p> <p class=$ Daarom is het relatieve uiterste van

$\bm{x=3}$

Dit is een minimum , aangezien

$f''(3)$

Het is positief.

Wat is de concaviteit en convexiteit van een functie?

Hoe de kromming van een functie te bestuderen

Voorbeeld van hoe u de kromming van een functie kunt vinden

Opgeloste oefeningen over de concaviteit en convexiteit van een functie

Oefening 1

Oefening 2

Oefening 3

Laat een reactie achter Reactie annuleren