In dit artikel zullen we zien hoe we de vergelijking van de raaklijn aan een curve kunnen vinden . Daarnaast kun je trainen met opgeloste oefeningen van verschillende moeilijkheidsgraden.
Vergelijking van de raaklijn aan een functie in een punt
De vergelijking van de raaklijn aan de functie f(x) in het punt x=x 0 is:
![]()
Waarbij het punt P(x 0 ,y 0 ) het punt is waar de raaklijn en de functie samenvallen. En de helling van de raaklijn, m, is gelijk aan de afgeleide van de curve op het punt x 0 , dat wil zeggen m=f'(x 0 ).

In de afbeelding hierboven zie je een curve
![]()
weergegeven in blauw en een oranje lijn die raakt aan de functie
![]()
Over
![]()
, omdat ze alleen dit punt gemeen hebben. Welnu, de vergelijking van deze raaklijn is
![]()
, en de helling ervan is
![]()
.
Hoe de raaklijnvergelijking te vinden
Om de vergelijking van de raaklijn aan een functie in een punt te vinden, moet je het volgende doen:
- Vind de helling van de raaklijn door de afgeleide van de functie op het raakpunt te berekenen.
- Bepaal een punt op de raaklijn.
- Zoek de vergelijking van de raaklijn met behulp van de berekende helling en het punt van de raaklijn.
Voorbeeld van de vergelijking van de raaklijn aan een curve
Nadat we de theorie over de raaklijnvergelijking hebben gezien, gaan we kijken hoe we de vergelijking van een raaklijn kunnen berekenen door stap voor stap een voorbeeld op te lossen:
- Bereken de vergelijking van de raaklijn aan de curve
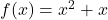
Over
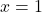
.
We weten dat de raaklijnvergelijking altijd de volgende vorm heeft:
![]()
Het eerste dat u moet doen, is de helling van de lijn berekenen. Dus de helling van de raaklijn,
![]()
, zal de waarde zijn van de afgeleide van de curve op het raakpunt x=1, dwz
![]()
We differentiëren daarom de functie en berekenen vervolgens
![]()
![]()
![]()
![]()
Zodra we de waarde ervan kennen
![]()
, we moeten een punt vinden
![]()
van de raaklijn om de vergelijking van de raaklijn te voltooien.
De vergelijking van de raaklijn en de curve hebben altijd een gemeenschappelijk punt , wat in dit geval zo is
![]()
. Daarom, zoals de curve
![]()
door dit punt gaat, kunnen we de andere component van het punt vinden door te berekenen
![]()
![]()
![]()
Het raakpunt is dus:
![]()
Zowel de curve als de raaklijn gaan door dit punt, dus we kunnen deze ook gebruiken om de vergelijking van de raaklijn te vinden.
Het enige dat overblijft is om de gevonden waarden van de helling en het punt van de raaklijn in de vergelijking te vervangen:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=3 \qquad P(1,2) \end{array} \right\} \longrightarrow \ y -2= 3(x-1)](https://mathority.org/wp-content/ql-cache/quicklatex.com-0321e19825c08a1f47a00b2cf625088f_l3.png)
Kort gezegd is de raaklijnvergelijking:
![]()
Je kunt de vergelijking van de raaklijn ook uitdrukken met de expliciete vergelijking van de lijn:
![]()
Hieronder ziet u de curve weergegeven
![]()
en de lijn die raakt aan
![]()
![]()
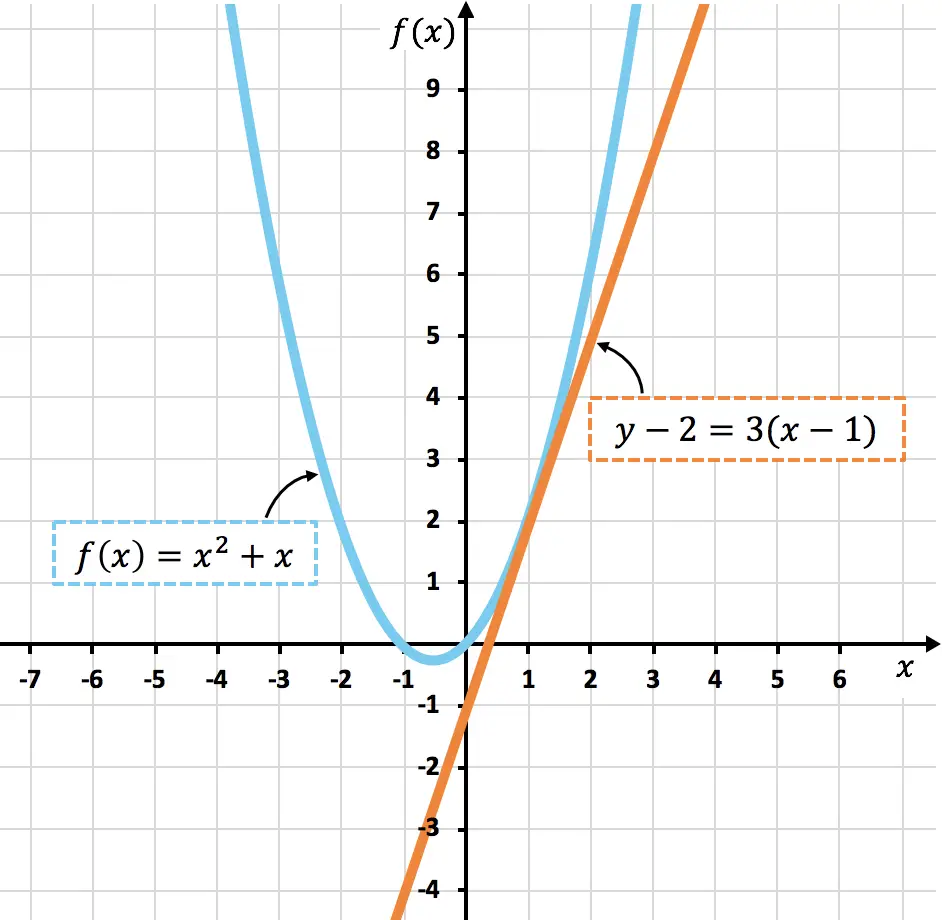
Zoals je kunt zien, de curve
![]()
en de raaklijn
![]()
ze hebben alleen het punt gemeen
![]()
, precies zoals we hadden berekend.
Opgeloste oefeningen over de raaklijnvergelijking
Oefening 1
Bereken de vergelijking van de raaklijn aan de curve
![]()
Over
![]()
De raaklijnvergelijking heeft altijd de volgende vorm:
![]()
Stap 1: Bereken de helling van de raaklijn
De helling, m , is de waarde van de afgeleide van de curve op het raakpunt. Daarom in dit geval
![]()
![]()
![]()
![]()
Stap 2: Zoek een punt op de raaklijn
De vergelijking van de raaklijn en de curve hebben altijd een gemeenschappelijk punt, wat in dit geval het geval is
![]()
. Daarom, zoals de curve
![]()
door dit punt gaat, kunnen we de andere component van het punt vinden door te berekenen
![]()
![]()
![]()
Het punt waar zowel de curve als de raaklijn doorheen gaan, is dus het punt
![]()
Stap 3: Schrijf de raaklijnvergelijking
Het enige dat overblijft is om de gevonden waarden van de helling en het punt van de raaklijn in de vergelijking te vervangen:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(2,3) \end{array} \right\} \longrightarrow \ y -3= 4(x-2)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1622c6ecd4d43bb4fc4901b437464652_l3.png)
De raaklijnvergelijking is daarom:
![]()
Oefening 2
Bereken de vergelijking van de raaklijn aan de curve
![]()
op de oorsprong van de coördinaten.
De oorsprong van de coördinaten verwijst naar het punt
![]()
We moeten daarom de raaklijn aan de functie op het punt berekenen
![]()
Eerst bepalen we de waarde van de helling van de raaklijn door de afgeleide aan de oorsprong van de coördinaten te berekenen:
![]()
![]()
![]()
In dit geval kennen we al een punt waar de raaklijn doorheen gaat. Omdat de verklaring ons vertelt dat de lijn de curve moet raken op de oorsprong van de coördinaten, dat wil zeggen op het punt
![]()
Dus het punt dat de curve en de raaklijn delen, is het punt
![]()
Vervang ten slotte eenvoudigweg de gevonden waarden voor de helling en het raakpunt in uw vergelijking:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=2 \qquad P(0,0) \end{array} \right\} \longrightarrow \ y -0= 2(x-0)](https://mathority.org/wp-content/ql-cache/quicklatex.com-de8e4e9dbb7a5bca1d591612abcf7730_l3.png)
Concluderend is de raaklijnvergelijking:
![]()
![]()
Oefening 3
Bereken de raaklijn aan de curve
![]()
die evenwijdig is aan de rechterkant
![]()
.
In dit probleem wordt ons verteld dat de raaklijn evenwijdig moet zijn aan de lijn
![]()
En twee lijnen zijn evenwijdig als ze dezelfde helling hebben. De raaklijn moet dus dezelfde helling hebben als de lijn
![]()
Dit betekent dat we de helling van de lijn moeten vinden
![]()
Om dit te doen, wissen we de variabele en:
![]()
Dus de helling van de lijn
![]()
is 4, omdat de helling van een lijn het getal is dat de x vermenigvuldigt wanneer de y helder is.
Daarom moet de helling van de raaklijn ook 4 zijn, omdat ze, om evenwijdig te zijn, dezelfde helling moeten hebben.
![]()
In dit geval vertellen ze ons niet het raakpunt tussen de curve en de raaklijn. Maar we weten dat de afgeleide van de curve op het raakpunt gelijk is aan de helling van de raaklijn, dwz
![]()
. Hoe kunnen we de waarde van weten?
![]()
, kunnen we x 0 uit de vergelijking vinden
![]()
Om dit te doen, berekenen we eerst de afgeleide van
![]()
![]()
En nu lossen we het op
![]()
wetende dat
![]()
![]()
![]()
![]()
![]()
![]()
![]()
En zodra we de x-coördinaat van het punt kennen, kunnen we de andere coördinaat van het punt vinden door te berekenen
![]()
![]()
Het punt waar zowel de curve als de raaklijn doorheen gaan, is dus het punt
![]()
Het enige dat overblijft is om de gevonden waarden van de helling en het punt van de raaklijn in de vergelijking te vervangen:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=4 \qquad P(3,2) \end{array} \right\} \longrightarrow \ y -2= 4(x-3)](https://mathority.org/wp-content/ql-cache/quicklatex.com-8f1f49e9bef505c5c71cffd15f0d29d0_l3.png)
En de vergelijking van de raaklijn is:
![]()
Oefening 4
Bereken de raaklijn aan de curve
![]()
die een hoek van 45° vormt met de X-as.
De probleemstelling vertelt ons dat de raaklijn een hoek van 45° moet vormen met de X-as. In deze gevallen moet de volgende formule worden toegepast om de waarde van de helling te vinden:
![]()
![]()
De verklaring specificeert niet het raakpunt tussen de curve en de raaklijn. Maar we weten dat de afgeleide van de curve op het raakpunt gelijk is aan de helling van de raaklijn, dwz
![]()
. We kunnen daarom x 0 berekenen door de vergelijking op te lossen
![]()
Om dit te doen, berekenen we eerst de afgeleide van
![]()
![]()
En nu lossen we het op
![]()
wetende dat
![]()
![]()
![]()
![]()
![]()
![]()
![]()
En zodra we de x-coördinaat van het punt kennen, kunnen we de andere coördinaat van het punt vinden door te berekenen
![]()
![]()
Het punt waar zowel de curve als de raaklijn doorheen gaan, is dus het punt
![]()
Het enige dat overblijft is om de gevonden waarden van de helling en het punt van de raaklijn in de vergelijking te vervangen:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} y -y_0= m(x-x_0) \\[3ex] m=1 \qquad P(-1,-2) \end{array} \right\} \longrightarrow \ y -(-2)= 1(x-(-1))](https://mathority.org/wp-content/ql-cache/quicklatex.com-8ed772b3993de50c4c67631a6fd33040_l3.png)
En ten slotte voeren we de bewerkingen uit om de vergelijking van de raaklijn te vinden:
![]()
![]()
![]()