In dit artikel leer je hoe je de differentieerbaarheid van een functie kunt bestuderen, dat wil zeggen of een functie differentieerbaar is of niet. Daarnaast zullen we de relatie zien tussen differentiatie en continuïteit van een functie. En ten slotte zullen we de differentieerbaarheid van een stuksgewijze functie bestuderen.
Differentieerbaarheid en continuïteit van een functie
De continuïteit en differentieerbaarheid van een functie op een punt zijn als volgt gerelateerd:
- Als een functie op een bepaald punt differentieerbaar is, is de functie op dat punt continu.
- Als een functie op een bepaald punt niet continu is, is deze op dat punt ook niet differentieerbaar.
Het omgekeerde van deze stelling is echter onjuist: het feit dat een functie op een bepaald punt continu is, betekent niet dat deze op dat punt altijd differentieerbaar is.
Je kunt ook zien of een functie op een bepaald punt wel of niet differentieerbaar is vanuit de grafische weergave:
- Als het een glad punt is, is de functie op dit punt differentieerbaar.
- Als het een hoekpunt is, is de functie continu maar op dit punt niet differentieerbaar.

Afvlakkingspunt op x=0:
continue en differentieerbare functie in dit stadium.

Hoekpunt op x=2:
functie continu maar niet differentieerbaar in dit stadium.
Differentieerbaarheid van een stuksgewijze functie
Zodra we de relatie tussen continuïteit en differentieerbaarheid van een functie kennen, zullen we zien hoe we de differentieerbaarheid van een stuksgewijs gedefinieerde functie kunnen bestuderen.
Je kunt zien of een stuksgewijze functie op een bepaald punt differentieerbaar is door de laterale afgeleiden op dat punt te berekenen:
- Als de laterale afgeleiden op een punt niet gelijk zijn, is de functie op dat punt niet differentieerbaar:
![]()
Het is niet aftrekbaar binnen
![]()
- Als de laterale afgeleiden op een punt samenvallen, is de functie op dat punt differentieerbaar:
![]()
Ja, het is differentieerbaar in
![]()
Opmerking: Om een functie op een bepaald punt differentieerbaar te maken, moet de functie op dat punt continu zijn. Voordat we de laterale afgeleiden berekenen, moeten we er daarom voor zorgen dat de functie op dat punt continu is. Als u niet weet hoe continuïteit op een bepaald punt wordt bestudeerd, kunt u zien hoe dit wordt gedaan in de volgende link:
Laten we nu een voorbeeld bekijken van hoe je de afgeleide kunt berekenen van een functie die stuksgewijs op een punt is gedefinieerd:
- Bestudeer de continuïteit en differentieerbaarheid van de volgende functie, stuksgewijs gedefinieerd op het punt x=2:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
De functies van de twee delen zijn continu in hun respectieve intervallen, maar het is noodzakelijk om te zien of de functie continu is op het kritieke punt x = 2. Om dit te doen, lossen we de laterale grenzen van de functie op op het punt:
![]()
![]()
De laterale grenzen op het kritieke punt gaven ons hetzelfde resultaat, dus de functie is continu op het punt x=2.
Zodra we weten dat de functie continu is op x=2, zullen we de differentieerbaarheid van de functie op dat punt bestuderen. Om dit te doen, berekenen we de laterale afgeleiden van de functie die in stukken is gedefinieerd:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
We evalueren nu elke laterale afgeleide op het kritieke punt:
![]()
![]()
De twee laterale afgeleiden gaven ons hetzelfde resultaat, dus de functie is differentieerbaar op x=2 en de waarde van de afgeleide is 6:
![]()
Aan de andere kant, als de laterale afgeleiden ons een ander resultaat hadden opgeleverd, zou dit betekenen dat de functie niet differentieerbaar is op x=2. Met andere woorden: de afgeleide zou op dit moment niet bestaan.
Bedenk ten slotte dat deze procedure ook geldig is voor het bestuderen van de differentieerbaarheid van een absolute-waardefunctie, aangezien absolute-waardefuncties ook stuksgewijs kunnen worden gedefinieerd. Je kunt hier zien hoe je een absolute-waardefunctie naar chunks converteert:
➤ Zie: hoe u een functie met een absolute waarde stuksgewijs definieert
Opgeloste oefeningen over de differentieerbaarheid van een functie
Oefening 1
Bestudeer de continuïteit en differentieerbaarheid van de volgende stuksgewijze functie:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
De functies van de twee delen zijn continu, maar we moeten kijken of de functie continu is op het kritieke punt x=1. Om dit te doen lossen we de laterale grenzen van de functie op op het punt:
![]()
![]()
De twee laterale grenzen op het kritieke punt geven hetzelfde resultaat, dus de functie is continu op x=1.
Zodra we weten dat de functie op het kritieke punt continu is, zullen we onderzoeken of deze op hetzelfde punt differentieerbaar is. We berekenen daarom de laterale afgeleiden:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
En we evalueren de twee laterale afgeleiden op x=1;
![]()
![]()
De laterale afgeleiden vallen niet samen op het punt x=1, dus de functie is op dit punt niet differentieerbaar.
![]()
Oefening 2
Analyseer de differentiatie en continuïteit van de volgende functie, gedefinieerd in secties:
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”226″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
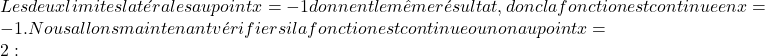
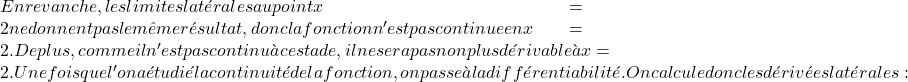
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)