Afgeleide van een quotiënt (deling): formule en opgeloste oefeningen

In dit artikel leggen we uit hoe je uit twee functies een quotiënt (of deling) kunt afleiden. Je vindt voorbeelden van afgeleiden van quotiënten van functies en daarnaast kun je oefenen met stapsgewijze oefeningen over afgeleiden van delingen.

Formule voor de afgeleide van een quotiënt

De afgeleide van een coëfficiënt (of deling) van de functies is identiek aan de afgeleide van de tellerfunctie door de noemerfunctie kleiner dan de tellerfunctie door de afgeleide van de noemerfunctie gedeeld door het kwadraat van de hoge noemerfunctie.

formule voor de afgeleide van een deling of quotiënt

Zoals je kunt zien, hebben we na differentiatie nog steeds een breuk als we de regel voor de afgeleide van een quotiënt (of deling) toepassen. Maar bovendien hebben we in de teller twee vermenigvuldigingen en een aftrekking, en de noemer wordt verheven tot de macht twee.

Voorbeelden van afgeleiden van quotiënten

We hebben zojuist gezien wat de formule is voor de afgeleide van een quotiënt van twee functies. Vervolgens zullen we verschillende voorbeelden van afgeleiden van dit soort bewerkingen oplossen. Houd er rekening mee dat als u niet begrijpt hoe een functioneel quotiënt wordt afgeleid, u ons dit kunt vragen in het opmerkingengedeelte.

voorbeeld 1

In dit voorbeeld zullen we een potentiële functie afleiden gedeeld door een trigonometrische functie:

$f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}$

De formule voor de afgeleide van een deling van twee verschillende functies is als volgt:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

We moeten dus eerst de afgeleide van elke functie afzonderlijk berekenen:

$\cfrac{d}{dx}\ (3x^2+4x)=6x+4$

$\cfrac{d}{dx}\ \text{sen}(2x)=2\text{cos}(2x)$

De afgeleide van de gehele functie is daarom:

$\begin{array}{c}f(x)=\cfrac{3x^2+4x}{\text{sen}(2x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(6x+4)\cdot\text{sen}(2x)-(3x^2+4x)\cdot 2\text{cos}(2x)}{\text{sen}^2(2x)}\end{array}$

Voorbeeld 2

In dit geval vinden we de afgeleide van een constante gedeeld door een functie:

$f(x)=\cfrac{10}{x^2+3x-9}$

Zoals we hierboven hebben gezien, is de regel voor de afgeleide van een deling van twee verschillende functies als volgt:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

We berekenen dus afzonderlijk de afgeleide van de teller en de noemer:

$\cfrac{d}{dx}\ 10=0$

$\cfrac{d}{dx}\ (x^2+3x-9)=2x+3$

En tenslotte vinden we de afgeleide van de deling van gehele getallen:

$\begin{array}{c}f(x)=\cfrac{10}{x^2+3x-9}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{0\cdot (x^2+3x-9)-10\cdot (2x+3)}{\left(x^2+3x-9\right)^2}=\cfrac{-20x+30}{\left(x^2+3x-9\right)^2}\end{array}$

In feite kunnen we een formule afleiden om direct te differentiëren als we een constante in de teller hebben gedeeld door een functie, omdat de afgeleide van de constante altijd 0 is. Daarom zal de volgende formule altijd waar zijn:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=\cfrac{k}{f(x)} \\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{-k\cdot f'(x)}{\bigl(f(x)\bigr)^2}\end{array} \end{empheq}$

Voorbeeld 3

In deze oefening zullen we een quotiënt van twee polynomen afleiden:

$f(x)=\cfrac{x^3+4x^2}{5x^2-8}$

Om de afgeleide op te lossen, moeten we de regel toepassen voor de afgeleide van een quotiënt van twee verschillende functies, die als volgt luidt:

$\begin{array}{c}z(x)=\cfrac{f(x)}{g(x)}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=\cfrac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}\end{array}$

Laten we nu de afgeleide van het tellerpolynoom en het noemerpolynoom vinden:

$\cfrac{d}{dx}\ (x^3+4x^2)=3x^2+8x$

$\cfrac{d}{dx}\ (5x^2-8)=10x$

De afgeleide van de verdeling van polyniemen is daarom:

$\begin{array}{c}f(x)=\cfrac{x^3+4x^2}{5x^2-8}\\[2.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\end{array}$

En ten slotte voeren we de bewerkingen uit en vereenvoudigen we de breuk zoveel mogelijk:

$\begin{aligned}f'(x)&=\cfrac{(3x^2+8x)\cdot (5x^2-8)-(x^3+4x^2)\cdot 10x}{\left(5x^2-8\right)^2}\\[2ex]&=\cfrac{15x^4-24x^2+40x^3-64x-10x^4-40x^3}{25x^4+64-80x^2}\\[2ex]&=\cfrac{5x^4-24x^2-64x}{25x^4-80x^2+64}\end{aligned}$

Opgeloste oefeningen over de afgeleide van een quotiënt

Leid de volgende functieverdelingen af:

$\text{A) }f(x)=\cfrac{9x^2+5x}{6x^3}$

$\text{B) }f(x)=\cfrac{19}{2x^2-2}$

$\text{C) }f(x)=\cfrac{8x^3-4x^2+3x}{e^{4x}}$

$\text{D) }f(x)=\cfrac{\text{cos}(x^2)}{\text{sen}(6x)}$

$\text{E) }f(x)=\cfrac{\ln(x^3+4)}{\left(4x^2-3x\right)^3}$

$\text{F) }f(x)=\cfrac{\sqrt{x^2+4x}}{5^{x^2}}$

Zie de oplossing

$\begin{aligned}\text{A) }f'(x)&=\cfrac{(18x+5)\cdot 6x^3-(9x^2+5x)\cdot 18x^2}{\left(6x^3\right)^2}\\[1.5ex]&=\cfrac{108x^4+30x^3-162x^4-90x^3}{36x^6}\\[1.5ex]&=\cfrac{-54x^4-60x^3}{36x^6}\\[1.5ex]&=\cfrac{-9x-10}{6x^3}\end{aligned}$

$\text{B) }f'(x)=\cfrac{-19\cdot 4x}{\left(2x^2-2\right)^2}=\cfrac{-76x}{\left(2x^2-2\right)^2}$

$\begin{aligned}\text{C) }f'(x)&=\cfrac{(24x^2-8x+3)e^{4x}-(8x^3-4x^2+3x)\cdot 4e^{4x}}{\left(e^{4x}\right)^2}\\[1.5ex]&=\cfrac{e^{4x}(24x^2-8x+3-32x^3+16x^2-12x)}{e^{8x}}\\[1.5ex]&=\cfrac{-32x^3+40x^2-20x+3}{e^{4x}}\end{aligned}$

$\text{D) }f'(x)=\cfrac{-2x\text{sen}(x^2)\cdot\text{sen}(6x)-\text{cos}(x^2)\text{cos}(6x)\cdot 6}{\text{sen}^2(6x)}$

$\begin{aligned}\text{E) }f'(x)&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(\left(4x^2-3x\right)^3\right)^2}\\[1.5ex]&=\cfrac{\cfrac{3x^2}{x^3+4}\cdot\left(4x^2-3x\right)^3-\ln(x^3+4)\cdot 3\left(4x^2-3x\right)^2\cdot (8x-3) }{\left(4x^2-3x\right)^6}\end{aligned}$

$\begin{aligned}\text{F) }f'(x)&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{\left(5^{x^2}\right)^2}\\[1.5ex]&=\cfrac{\cfrac{2x+4}{2\sqrt{x^2+4x}}\cdot 5^{x^2} - \sqrt{x^2+4x}\cdot 5^{x^2}\cdot \ln(5) \cdot 2x }{5^{2x^2}}\end{aligned}$

Demonstratie van de afgeleide van een quotiënt

Ten slotte zullen we de formule demonstreren voor de afgeleide van een deling. Om dit te doen, zullen we de algemene definitie van een derivaat gebruiken, namelijk:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Laat z een deling zijn van twee verschillende functies:

$z(x)=\cfrac{f(x)}{g(x)}$

Dan zal de afgeleide van de functie z, waarbij de wiskundige definitie wordt toegepast, zijn:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)}{g(x+h)}-\cfrac{f(x)}{g(x)}}{h}$

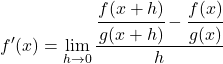
We lossen het aftrekken van breuken op van de teller van de breuk:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{\cfrac{f(x+h)\cdot g(x)}{g(x+h)\cdot g(x)}-\cfrac{f(x)\cdot g(x+h)}{g(x)\cdot g(x+h)}}{h}$

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x+h)}{h\cdot g(x)\cdot g(x+h)}$

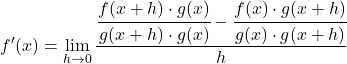
Het toevoegen van een optel- en aftrekkingsterm aan een vergelijking verandert de vergelijking niet. We kunnen daarom doorgaan naar de volgende stap:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x)\color{orange}\bm{-f(x)\cdot g(x)}\color{black}-f(x)\cdot g(x+h)\color{orange}\bm{+f(x)\cdot g(x)}\color{black}}{h\cdot g(x)\cdot g(x+h)}$

We halen de gemeenschappelijke factor eruit:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\bigl[f(x+h)-f(x)\bigr]-f(x)\bigl[g(x+h)-g(x)\bigr]}{h\cdot g(x)\cdot g(x+h)}$

Laten we nu de term h van de noemer naar de teller verplaatsen met behulp van de eigenschappen van breuken:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{g(x)\cdot \cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot g(x+h)}$

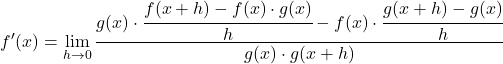
We transformeren de vergelijking door de eigenschappen van de limieten toe te passen:

$\displaystyle f'(x)=\frac{g(x)\cdot \displaystyle\lim_{h \to 0}\cfrac{f(x+h)-f(x)\cdot g(x)}{h}-f(x)\cdot\lim_{h \to 0}\cfrac{g(x+h)-g(x)}{h}}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

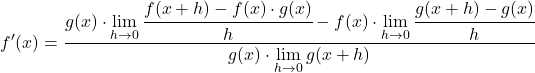
De grenzen van de teller komen precies overeen met de wiskundige definitie van de afgeleide van elke functie, dus:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot \displaystyle\lim_{h \to 0}g(x+h)}$

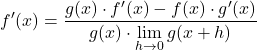
We lossen de limiet van de noemer van de breuk op:

$\displaystyle f'(x)=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{g(x)\cdot g(x)}$

En zo wordt de formule voor de afgeleide van een quotiënt van twee functies gedemonstreerd:

$\displaystyle f'(x)=\frac{f'(x)\cdot g(x)-f(x)\cdot g'(x)}{\bigl(g(x)\bigr)^2}$

Afgeleide van een quotiënt (of deling)

Formule voor de afgeleide van een quotiënt

Voorbeelden van afgeleiden van quotiënten

voorbeeld 1

Voorbeeld 2

Voorbeeld 3

Opgeloste oefeningen over de afgeleide van een quotiënt

Demonstratie van de afgeleide van een quotiënt

Laat een reactie achter Reactie annuleren