▷ Afgeleide van een aftrekking (formule en opgeloste oefeningen)

In dit artikel leggen we uit hoe je een aftrekking van functies kunt afleiden (formule). Je vindt er ook voorbeelden van aftrekkingsafgeleiden en opgeloste stap-voor-stapoefeningen om te oefenen.

Formule voor de afgeleide van een aftrekking

De afgeleide van het aftrekken van twee functies is gelijk aan het aftrekken van de afgeleide van elke functie afzonderlijk.

$z(x)=f(x)-g(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=f'(x)-g'(x)$

Met andere woorden, het afzonderlijk differentiëren van twee functies en ze vervolgens van elkaar aftrekken, komt neer op het eerst aftrekken van de functies en vervolgens het nemen van de afgeleide.

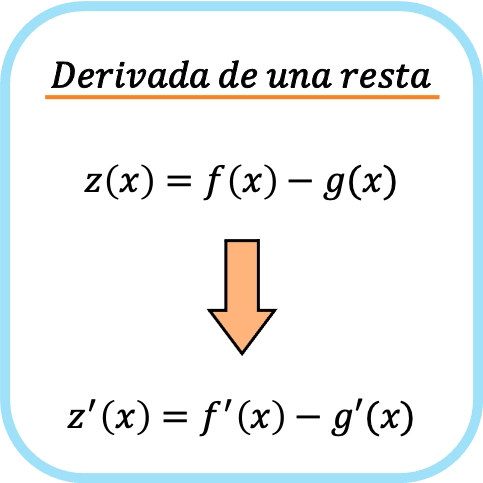
Op dezelfde manier is dezelfde differentiatieregel van toepassing op het aftrekken van twee of meer functies, dus als we een aftrekking hebben van drie, vier, vijf,… functies, moeten we ze afzonderlijk differentiëren en ze vervolgens aftrekken.

$\begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}$

Zoals je ziet lijkt de formule voor de afgeleide van een verschil tussen functies sterk op de regel voor de afgeleide van een som.

➤ Zie:afgeleide van een som van functies

Voorbeelden van afgeleide van aftrekken

Zodra we hebben gezien wat de formule voor de afgeleide van een aftrekking is, gaan we nu verder met het analyseren van verschillende voorbeelden van afgeleiden van dit soort bewerkingen om volledig te begrijpen hoe de aftrekkingen van functies worden afgeleid.

Voorbeeld 1: Afgeleide van een aftrekking van potentiële functies

$f(x)=x^3-4x$

De afgeleide van het aftrekken van twee functies is gelijk aan het verschil tussen de afgeleiden van elke functie afzonderlijk. We zullen daarom eerst de afgeleide van elke functie afzonderlijk berekenen:

$\cfrac{d}{dx} \ x^3=3x^2$

$\cfrac{d}{dx}\ 4x=4$

De afgeleide van de gehele functie is daarom als volgt:

$f'(x)=3x^2-4$

Voorbeeld 2: Afgeleide van een aftrekking van verschillende functies

$f(x)=\text{cos}(x)-\log_7(x^2)$

Om aftrekkingsfuncties van elkaar te onderscheiden, moet u eerst de twee functies afzonderlijk differentiëren en ze vervolgens van elkaar aftrekken.

$\cfrac{d}{dx} \ \text{cos}(x)=-\text{sen}(x)$

$\cfrac{d}{dx}\ \log_7 (x^2)=\cfrac{2x}{x^2\cdot \ln(7)}=\cfrac{2}{x\ln(7)}$

En nadat we de twee afgeleiden hebben gemaakt, trekken we ze af met dezelfde initiële volgorde:

$f'(x)=-\text{sen}(x)-\cfrac{2}{x\ln(7)}$

Voorbeeld 3: Afgeleide van een kwadratische aftrekking

$f(x)=\left(x^7-2x^3-9\right)^2$

In dit geval hebben we een samengestelde functie, omdat het een aftrekking is tussen drie kwadraatfuncties. We moeten daarom de formule voor de afgeleide van een potentiële functie en de kettingregel gebruiken om de afgeleide van de gehele functie te berekenen:

$f(x)=2\left(x^7-2x^3-9\right)\cdot \left(7x^6-6x^2\right)$

➤ Zie: formule voor de afgeleide van een macht

Opgeloste oefeningen over de afgeleide van een aftrekking

Leid de volgende aftrekkingen van functies af:

$\text{A) } f(x)=9x^3-5x$

$\text{B) } f(x)=4x^5-6x^4-x^2-4$

$\text{C) } f(x)=\left(-3x^7-2x^5\right)^4$

$\text{D) } f(x)=\ln(5x^2+3x)-\text{cos}(x)$

$\text{E) } f(x)=8x^3-e^{5x}-\sqrt{8x+2}$

Zie de oplossing

$\text{A) } f'(x)=27x^2-5$

$\text{B) } f'(x)=20x^4-24x^3-2x$

$\text{C) } f'(x)=4\left(-3x^7-2x^5\right)^3\cdot (-21x^6-10x^4)$

$\text{D) } f'(x)=\cfrac{10x+3}{5x^2+3x}-\bilg(-\text{sen}(x)\bigr)=\cfrac{10x+3}{5x^2+3x}+\text{sen}(x)$

$\text{E) } f'(x)=24x^2-5e^{5x}-\cfrac{8}{2\sqrt{8x+2}}=24x^2-5e^{5x}-\cfrac{4}{\sqrt{8x+2}}$

Bewijs van de afgeleide van een aftrekking

Vervolgens zullen we de formule demonstreren voor de afgeleide van een aftrekking van functies van de definitie van de afgeleide, namelijk:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Dus als z het verschil is tussen twee verschillende functies:

$z(x)=f(x)-g(x)$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{z(x+h)-z(x)}{h}$

We vervangen z door het aftrekken van de functies in de limietuitdrukking:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)-g(x+h)\bigr]-\bigl[f(x)-g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-g(x+h)-f(x)+g(x)}{h}$

We zullen nu een transformatie uitvoeren om de breuk te scheiden en een aftrekking van twee breuken te verkrijgen:

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}+\frac{-g(x+h)+g(x)}{h}\right]$

$\displaystyle z'(x)=\lim_{h \to 0}\left[\frac{f(x+h)-f(x)}{h}-\frac{g(x+h)-g(x)}{h}\right]$

Door de wetten van limieten toe te passen, kunnen we de bovenstaande uitdrukking in twee verschillende limieten verdelen. Omdat de limiet van een aftrekking gelijk is aan de aftrekking van limieten:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}-\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}$

Als je goed kijkt, komt elke limiet overeen met de afgeleide van een functie, wat betekent dat aan de formule voor de afgeleide van een verschil is voldaan:

$\displaystyle z'(x)=f'(x)-g'(x)$