▷ Afgeleide van de boogtangens (formule en voorbeelden)

In dit artikel leer je hoe je de boogtangens van een functie afleidt. Bovendien kun je voorbeelden van dit soort afgeleiden zien en zelfs oefenen met opgeloste oefeningen over de afgeleide van de boogtangens. Ten slotte laten we u ook het bewijs zien van de formule voor de afgeleide van de boogtangens.

Wat is de afgeleide van de boogtangens?

De afgeleide van de boogtangens van x is één gedeeld door één plus x kwadraat.

$f(x)=\text{arctan}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1+x^2}$

Daarom is de afgeleide van de boogtangens van een functie gelijk aan het quotiënt van de afgeleide van die functie gedeeld door één plus de genoemde functie in het kwadraat.

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

In dit geval werd de functie weergegeven door au, dus dit zou de formule zijn voor de afgeleide van de boogtangens van de functie u.

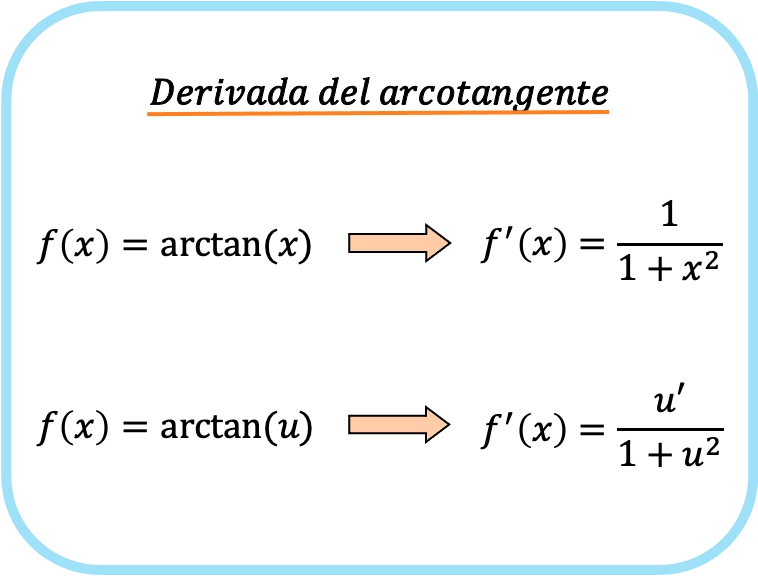
Zoals je kunt zien, lijkt de formule voor de afgeleide van de inverse tangens sterk op de formules voor de afgeleiden van arcsinus en arccosinus.

Voorbeelden van afgeleide van de boogtangens

Zodra we de formule kennen voor de afgeleide van de boogtangens, zullen we de afleiding van verschillende voorbeelden van dit soort trigonometrische afgeleiden uitleggen. Op deze manier wordt het gemakkelijker voor u om te begrijpen hoe de boogtangens van een functie wordt afgeleid.

Voorbeeld 1: Afgeleide van de boogtangens van 2x

$f(x)=\text{arctan}(2x)$

We passen de formule toe om de afgeleide op te lossen:

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

De afgeleide van 2x is 2, dus de boogtangensafgeleide van 2x is 2 gedeeld door één plus 2x kwadraat:

$f(x)=\text{arctan}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{1+(2x)^2}}=\cfrac{2}{1+ 4x^2}$

Voorbeeld 2: Afgeleide van de boogtangens van x kwadraat

$f(x)=\text{arctan}(x^2)$

Om het resultaat van de afgeleide van dit voorbeeld te vinden, moeten we de formule voor de afgeleide van de boogtangens gebruiken, namelijk:

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

De afgeleide van de functie x ² is dus 2x, dus de afgeleide van de boogtangens van x verheven tot de macht 2 is:

$f(x)=\text{arctan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{1+\left(x^2\right)^2}=\cfrac{2x}{1+x^4}$

Voorbeeld 3: Afgeleide van de boogtangens van de sinus van x

$f(x)=\text{arctan}\bigl(\text{sen}(x)\bigr)$

Om de afgeleide te berekenen, moet u logischerwijs de bijbehorende formule toepassen:

$f(x)=\text{arctan}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

In dit geval hebben we een samengestelde functie, dus moeten we de kettingregel toepassen om de afgeleide van de boogtangens te berekenen:

$f(x)=\text{arctan}\bigl(\text{sen}(x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{\text{cos}(x)}{1+\text{sen}^2(x)}$

Opgeloste oefeningen over de afgeleide van de boogtangens

Leid de volgende boogtangensfuncties af:

$\text{A) } f(x)=\text{arctan}(x^3)$

$\text{B) } f(x)=\cfrac{\text{arctan}(3x^4)}{2}$

$\text{C) } f(x)=\text{arctan}(x^5-3x^3+10)$

$\text{D) }f(x)=\text{arctan}^3(4x^2)$

$\text{E) }f(x)=\text{arctan}\bigl(\ln(x)\bigr)$

$\text{F) } f(x)=\text{arctan}\left(\sqrt{x^2+2x}\right)$

Zie de oplossing

$\text{A) } f'(x)=\cfrac{3x^2}{1+\left(x^3\right)^2}=\cfrac{3x^2}{1+x^6}$

$\text{B) } f'(x)=\cfrac{12x^3}{2\left(1+\left(3x^4\right)^2\right)}=\cfrac{6x^3}{1+9x^8}$

$\text{C) } f'(x)=\cfrac{5x^4-9x^2}{1+\left(x^5-3x^3+10\right)^2}$

$\text{D) } f'(x)=3\text{arctan}^2(4x^2)\cdot \cfrac{8x}{1+\left(4x^2\right)^2}=\cfrac{24x\cdot\text{arctan}^2(4x^2)}{1+16x^2}$

$\text{E) } f'(x)=\cfrac{\cfrac{1}{x}}{1+\bigl(\ln(x)\bigr)^2}=\cfrac{1}{x\left(1+\ln^2(x)\right)}$

$\text{F) } f'(x)=\cfrac{1}{1+\left(\sqrt{x^2+2x}\right)^2}\cdot \cfrac{2x+2}{2\sqrt{x^2+2x}}=\cfrac{x+1}{\left(1+x^2+2x\right)\sqrt{x^2+2x}}$

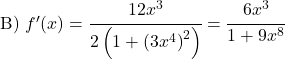
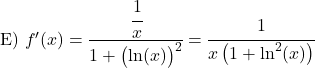
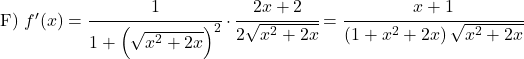
Demonstratie van de formule voor de afgeleide van de boogtangens

Vervolgens zullen we de formule bewijzen voor de afgeleide van de boogtangens.

$y=\text{arctan}(x)$

We converteren eerst de boogtangens naar een raaklijn, waarbij we profiteren van het feit dat de boogtangens de inverse functie van de raaklijn is:

$x=\text{tan}(y)$

We onderscheiden de twee kanten van de vergelijking:

$1=\cfrac{1}{\text{cos}^2(y)}\cdot y'$

We wissen en’:

$y'=\text{cos}^2(y)$

Aan de andere kant weten we dankzij de fundamentele trigonometrische identiteit dat de som van de kwadraten van de sinus en de cosinus gelijk is aan 1. We kunnen daarom de vorige uitdrukking omzetten in een breuk:

$\text{sen}^2(y)+\text{cos}^2(y)=1$

$y'=\cfrac{\text{cos}^2(y)}{1}=\cfrac{\text{cos}^2(y)}{\text{sen}^2(y)+\text{cos}^2(y)}$

We delen alle termen door het kwadraat van de cosinus:

$y'=\cfrac{\cfrac{\text{cos}^2(y)}{\text{cos}^2(y)}}{\cfrac{\text{sen}^2(y)}{\text{cos}^2(y)}+\cfrac{\text{cos}^2(y)}{\text{cos}^2(y)}}$

$y'=\cfrac{1}{\cfrac{\text{sen}^2(y)}{\text{cos}^2(y)}+1}$

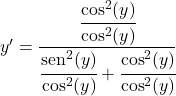
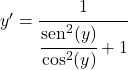
De sinus gedeeld door de cosinus is gelijk aan de tangens, dus:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

$y'=\cfrac{1}{\text{tan}^2(y)+1}$

Zoals we hierboven hebben gezien, is de raaklijn equivalent aan de variabele x. We kunnen daarom de uitdrukking vervangen om tot de formule voor de afgeleide van de boogtangens te komen:

$y'=\cfrac{1}{x^2+1}$

Wat is de afgeleide van de boogtangens?

Voorbeelden van afgeleide van de boogtangens

Voorbeeld 1: Afgeleide van de boogtangens van 2x

Voorbeeld 2: Afgeleide van de boogtangens van x kwadraat

Voorbeeld 3: Afgeleide van de boogtangens van de sinus van x

Opgeloste oefeningen over de afgeleide van de boogtangens

Demonstratie van de formule voor de afgeleide van de boogtangens

Laat een reactie achter Reactie annuleren