▷ Afgeleide van de raaklijn (formule en opgeloste oefeningen)

Hier leert u hoe de tangensfunctie wordt afgeleid. Bovendien kunt u voorbeelden zien van de afgeleide van de raaklijn en zelfs oefenen met oefeningen die stap voor stap worden opgelost. Ten slotte demonstreren we ook de raaklijnafgeleide formule en laten we u de inverse raaklijnafgeleide formule zien.

Wat is de afgeleide van de raaklijn?

De afgeleide van de raaklijn van x is gelijk aan 1 over het kwadraat van de cosinus van x. De afgeleide van de raaklijn van x is ook gelijk aan het kwadraat van de secans van x, en 1 plus het kwadraat van de raaklijn van x.

$\begin{array}{c}f(x)=\text{tan}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cos}^2(x)}=\text{sec}^2(x)=1+\text{tan}^2(x)\end{array}$

Alle uitdrukkingen zijn gelijkwaardig, dus de raaklijnfunctie heeft drie mogelijke formules om deze af te leiden.

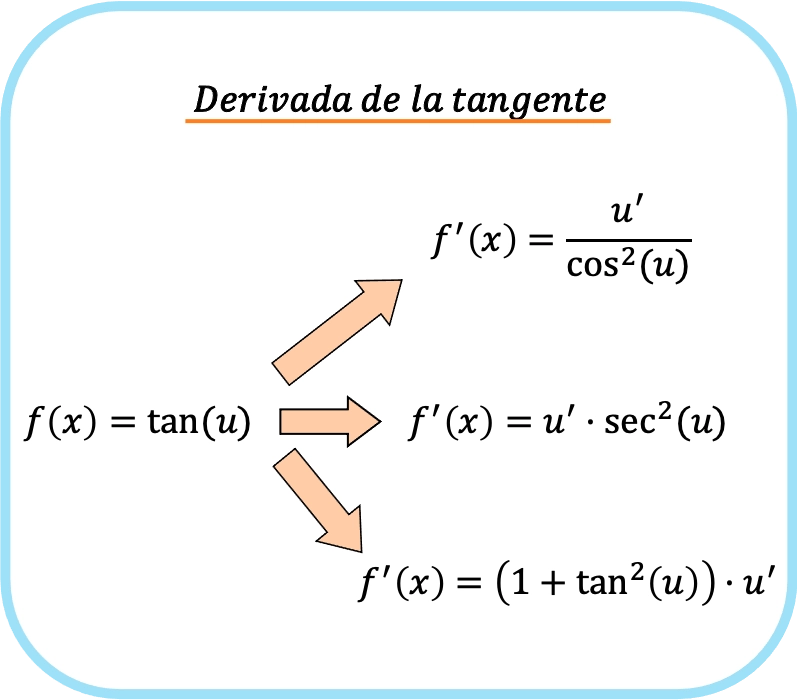
Aan de andere kant, als we in het raaklijnargument een andere functie hebben dan x (laten we het u noemen), moeten we de kettingregel toepassen. De afgeleide van de tangens van u is daarom:

$\begin{array}{c}f(x)=\text{tan}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cos}^2(u)}=\text{sec}^2(u)\cdot u'=\left(1+\text{tan}^2(u)\right)\cdot u'\end{array}$

Kort gezegd kan de raaklijnafgeleide regel als volgt worden samengevat:

Voorbeelden van raaklijnafgeleide

Gegeven de formule voor de raaklijnafgeleide, zullen we in deze sectie verschillende voorbeelden van dit soort trigonometrische afgeleiden oplossen, zodat u begrijpt hoe u de raaklijnfunctie kunt afleiden.

Voorbeeld 1: Afgeleide van de tangens van 2x

$f(x)=\text{tan}(2x)$

Om de afgeleide van de raaklijn te berekenen, kun je een van de drie formules gebruiken die we hierboven hebben gezien. In dit geval gebruiken we de cosinusformule:

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

De functie 2x is lineair, dus de afgeleide ervan is 2. Dus de afgeleide van de raaklijn van 2x is 2 over het kwadraat van de cosinus van 2x:

$f(x)=\text{tan}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\text{cos}^2(2x)}$

Voorbeeld 2: Afgeleide van de tangens van x in het kwadraat

$f(x)=\text{tan}(x^2)$

In dit voorbeeld is de tangens-argumentfunctie geen x, maar een functie met een afgeleide. Dat betekent dat we de kettingregel moeten toepassen om deze af te leiden.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

De afgeleide van x kwadraat is 2x, dus de afgeleide van de raaklijn van x ² is:

$f(x)=\text{tan}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\text{cos}^2(x^2)}$

Voorbeeld 3: Afgeleide van de raaklijn aan de kubus

$f(x)=\text{tan}^3(9x^2-4x)$

In dit probleem hebben we een samengestelde functie, dus we zullen ook de kettingregel moeten gebruiken om de raaklijn te differentiëren.

$f(x)=\text{tan}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\text{cos}^2(u)}$

Bovendien wordt de raaklijn verheven tot de macht 3, wat betekent dat voordat je de formule voor de afgeleide van de raaklijn toepast, je de formule voor de afgeleide van een macht moet gebruiken:

$\begin{aligned}f'(x)&=3\text{tan}^2(9x^2-4x)\cdot \cfrac{18x-4}{\text{cos}^2(9x^2-4x)} \\[2ex]&=\cfrac{3\text{tan}^2(9x^2-4x)\cdot(18x-4)}{\text{cos}^2(9x^2-4x)}\end{aligned}$

Afgeleide van de inverse tangens

Zoals elke inverse functie heeft de tangensfunctie ook een inverse, de arctangensfunctie. Hoewel de formule om deze af te leiden niet vergelijkbaar is met de raaklijnformule, laten we deze u zien omdat deze in sommige gevallen nuttig kan zijn.

De afgeleide van de inverse tangens van een functie is het quotiënt van de afgeleide van de functie gedeeld door één plus de genoemde functie in het kwadraat

$f(x)=\text{tan}^{-1}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1+u^2}$

De afgeleide van de inverse tangens van 3x is bijvoorbeeld:

$f(x)=\text{tan}^{-1}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{1+(3x)^2}=\cfrac{3}{1+9x^2}$

Opgeloste oefeningen over de afgeleide van de raaklijn

Bereken de afgeleide van de volgende raaklijnfuncties:

$\text{A) } f(x)=\text{tan}(3x)$

$\text{B) } f(x)=\text{tan}(x^3-10x^2+8)$

$\text{C) } \displaystyle f(x)=\text{tan}^2\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{tan}\left(e^{2x}\right)$

$\text{E) } f(x)=\text{tan}\bigl(\ln(4x)\bigr)$

$\text{F) } f(x)=\text{tan}\left(\sqrt{3x}\right)$

Zie de oplossing

$\text{A) } f'(x)=\cfrac{3}{\text{cos}^2(3x)}$

$\text{B) } f'(x)=\cfrac{3x^2-20x}{\text{cos}^2(x^3-10x^2+8)}$

$\text{C) } \displaystyle f'(x)=2\text{tan}\left(\frac{x}{2}\right)\cdot \frac{1}{\text{cos}^2\left(\frac{x}{2}\right)}\cdot \frac{1}{2}=\frac{\text{tan}\left(\frac{x}{2}\right)}{\text{cos}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=\cfrac{2e^{2x}}{\text{cos}^2(e^{2x})}$

$\text{E) } f'(x)=\cfrac{\frac{4}{4x}}{\text{cos}^2\bigl(\ln(4x)\bigr)}=\cfrac{1}{x\cdot\text{cos}^2\bigl(\ln(4x)\bigr)}$

$\text{F) } f'(x)=\cfrac{\frac{3}{2\sqrt{3x}}}{\text{cos}^2\left(\sqrt{3x}\right)}=\cfrac{3}{2\sqrt{3x}\cdot \text{cos}^2\left(\sqrt{3x}\right)}$

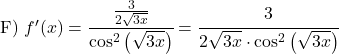
Bewijs van de afgeleide van de raaklijn

Zodat u kunt verifiëren dat dit geen verzonnen uitdrukking is, zullen we in deze sectie de formule voor de afgeleide van de raaklijn demonstreren met behulp van de wiskundige definitie van raaklijn.

Om dit te doen, gaan we uit van de trigonometrische identiteit die de drie trigonometrische verhoudingen met elkaar verbindt:

$\text{tan}(x)=\cfrac{\text{sen}(x)}{\text{cos}(x)}$

Als we de formule voor de afgeleide van een deling gebruiken, zou de afgeleide zijn:

$\displaystyle\left(\text{tan}(x)\right)'=\left(\frac{\text{sen}(x)}{\text{cos}(x)}\right)'$

$\text{tan}'(x)=\cfrac{\text{cos}(x)\cdot \text{cos}(x)+\text{sen}(x)\text{sen}(x) }{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

Maar door gebruik te maken van de fundamentele trigonometrische identiteit weten we dat het kwadraat van de sinus plus het kwadraat van de cosinus 1 is:

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{tan}'(x)=\cfrac{1}{\text{cos}^2(x)}$

En zo zijn we al aangekomen bij de eerste formule voor de afgeleide van de raaklijn. Bovendien is de secans de multiplicatieve inverse van de cosinus, dus wordt de tweede uitdrukking ook afgeleid:

$\text{tan}'(x)=\text{sec}^2(x)$

Ten slotte kan de derde regel van de raaklijnafgeleide worden bewezen door de breuk uit de vorige stap om te zetten in een som van breuken:

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)+\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=\cfrac{\text{cos}^2(x)}{\text{cos}^2(x)}+\cfrac{\text{sen}^2(x)}{\text{cos}^2(x)}$

$\text{tan}'(x)=1+\text{tan}^2(x)$

Wat is de afgeleide van de raaklijn?

Voorbeelden van raaklijnafgeleide

Voorbeeld 1: Afgeleide van de tangens van 2x

Voorbeeld 2: Afgeleide van de tangens van x in het kwadraat

Voorbeeld 3: Afgeleide van de raaklijn aan de kubus

Afgeleide van de inverse tangens

Opgeloste oefeningen over de afgeleide van de raaklijn

Bewijs van de afgeleide van de raaklijn

Laat een reactie achter Reactie annuleren