Hier leggen we uit hoe je een macht (of potentiële functie) kunt afleiden, vind je de formule voor de afgeleide van een macht, verschillende voorbeelden en kun je zelfs oefenen met oefeningen die stap voor stap worden opgelost.
Formule voor de afgeleide van een macht
De afgeleide van een macht, of potentiële functie, is het product van de exponent van de macht maal het grondtal verheven tot de exponent minus 1 maal de afgeleide van het grondtal.
![]()
Daarom, als de basis de identiteitsfunctie is, vermenigvuldigt u eenvoudigweg de functie met de exponent en trekt u één eenheid af van de exponent om de macht te krijgen:
![]()
De afgeleide van de identiteitsfunctie is inderdaad gelijk aan 1.
Samenvattend zijn er twee formules om een potentiële functie af te leiden: de eerste die altijd kan worden gebruikt en de tweede die alleen kan worden toegepast als de basis een x is.
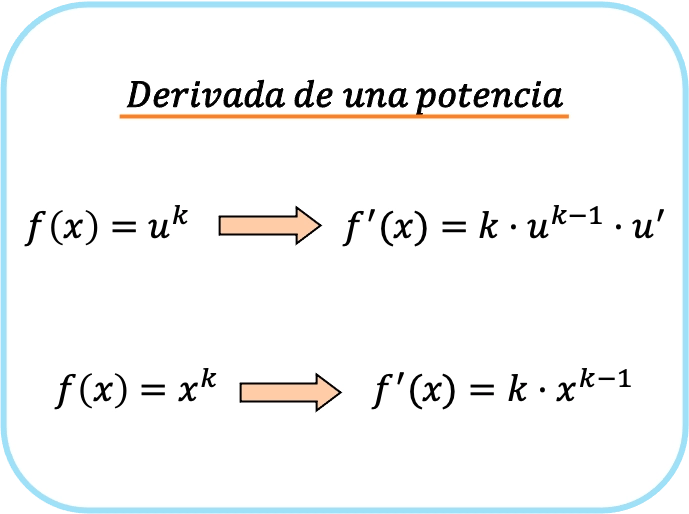
We kunnen gemakkelijk verifiëren dat de eerste formule die wordt gepresenteerd voor de afgeleide van een macht hetzelfde is als de tweede, maar dan met toepassing van de kettingregel.
Merk op dat deze formules alleen kunnen worden gebruikt als de variabele het grondtal van de macht is. Als de x in de noemer staat, moet je de regel toepassen voor de afgeleide van een exponentiële functie:
➤ Zie: afgeleide van een exponentiële functie
Voorbeelden van machtsderivaten
Zodra we de formule voor de afgeleide van een potentiële functie hebben gezien, zullen we verschillende voorbeelden van dit type afgeleide uitleggen, zodat je begrijpt hoe machten worden afgeleid.
Voorbeeld 1: Afgeleide van een basismacht x
![]()
Zoals we in de vorige sectie hebben uitgelegd, is de formule die we moeten gebruiken om de functie af te leiden als de basis van de macht slechts een x is:
![]()
De afgeleide van de macht x tot de macht 4 is daarom:
![]()
Voorbeeld 2: Afgeleide van een macht met haakjes
![]()
In dit voorbeeld is de basis niet de identiteitsfunctie, we moeten daarom de algemene formule gebruiken voor de afgeleide van een macht:
![]()
De functie tussen haakjes is een lineaire functie, dus de afgeleide ervan is 2. Daarom is de afgeleide van de gehele potentiële functie:
![]()
Voorbeeld 3: Afgeleide van een negatieve macht
![]()
In dit geval hebben we een potentiële functie waarvan de exponent negatief is en waarvan de basis een logaritme is, dus we zullen de volgende formule gebruiken om de functie te differentiëren:
![]()
Zelfs als de machtsexponent negatief is, moet er ook één van worden afgetrokken. De afgeleide van de functie is daarom:
![]()
Als u twijfelt over de oplossing, kunt u hier de formule voor de afgeleide van een logaritmische functie raadplegen:
➤ Zie: afgeleide van een logaritmische functie
Voorbeeld 4: Afgeleide van een macht met wortel
![]()
De functie in dit voorbeeld is een macht binnen een reguliere expressie. Radicalen kunnen echter worden omgezet in potentiële uitdrukkingen, dus de functie kan worden vereenvoudigd door deze om te zetten in een potentiële functie met een fractionele exponent:
![]()
We passen nu de formule toe voor de afgeleide van een macht van een variabele:
![]()
En de afgeleide is:
![]()
U kunt ook onderscheid maken tussen dit soort functies met behulp van de wortelafgeleideregel:
➤ Zie: afgeleid van een wortel
Opgeloste oefeningen over de afgeleide van een macht
Bereken de afgeleide van de volgende machten:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
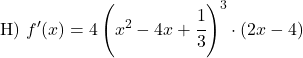
![]()