▷ Hoe limieten op oneindig op te lossen (+25 oefeningen opgelost)

Hier vindt u hoe u alle soorten limieten op oneindig kunt oplossen: polynomiale, rationale, exponentiële functies, met wortels, onbepaaldheid op oneindig… Daarnaast kunt u trainen met 25 oefeningen die stap voor stap worden opgelost over limieten wanneer x neigen naar het oneindige. .

Limiet van een functie wanneer x naar oneindig neigt

De limiet van een functie als x oneindig nadert , of deze nu positief of negatief is, kan een reële waarde zijn, plus oneindig, minus oneindig, of niet-bestaand. Om limieten op oneindig op te lossen, moet je x vervangen door oneindig.

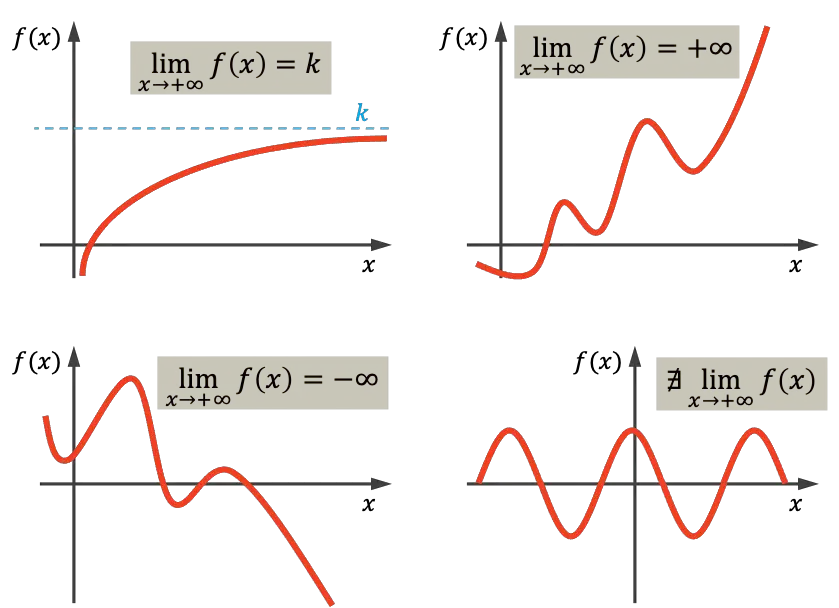
Zoals je in de eerste grafiek kunt zien, neigt de weergegeven functie naar de reële waarde k richting oneindig, omdat deze dichter bij k komt naarmate x groeit. De functie rechtsboven neigt naar oneindig naarmate x oneindig nadert, omdat deze voor onbepaalde tijd groeit naarmate x in waarde toeneemt. Aan de andere kant neemt de grafiek linksonder voortdurend af en neigt daarom naar min oneindig. Ten slotte is de laatste functie periodiek en neigt deze naar geen enkele waarde, dus er is in dit geval geen limiet aan oneindig.

Hoe limieten op oneindig op te lossen

Om een limiet tot oneindigheid in polynomiale functies op te lossen, moeten we x alleen vervangen door oneindigheid in de term van de hoogste graad van de functie.

Kijk bijvoorbeeld eens naar de volgende berekening van een limiet tot oneindigheid, waarbij we alleen oneindigheid vervangen door de monomiaal van de hoogste graad:

$\displaystyle \lim_{x \to +\infty}(3x^2-4x+6) = 3(+\infty)^2 = \bm{+\infty}$

Zoals je in het voorbeeld kunt zien, geeft +∞ kwadraat +∞, aangezien een heel groot getal (+∞) tot de macht 2 altijd een heel groot getal (+∞) oplevert.

En hetzelfde gebeurt met vermenigvuldigen: als je een heel groot getal (+∞) vermenigvuldigt, krijg je altijd een heel groot getal (+∞). Bijvoorbeeld:

$3\cdot (+\infty)= +\infty.$

Waarschuwing: om grenzen tot oneindig te berekenen is het belangrijk om rekening te houden met de volgende elementen:

→ Een negatief getal verhoogd tot een even exponent is positief. Daarom geeft min oneindig verhoogd tot een even exponent plus oneindig:

$(-\infty)^2 = +\infty$

→ Een negatief getal verheven tot een oneven exponent is negatief. Daarom is minus oneindig verhoogd tot een oneven exponent minus oneindig:

$(-\infty)^3 = -\infty$

→ Door een negatief getal te vermenigvuldigen verandert het teken van oneindig:

$-2(+\infty) = - \infty$

→ Elk getal gedeeld door

$\pm \infty$

geeft 0:

$\cfrac{5}{\infty} = 0$

Voorbeelden van limieten tot oneindig

Je kunt dus zien hoe limieten tot oneindig worden opgelost in polynomen. Hieronder zijn een aantal van dergelijke limieten opgelost:

$\begin{array}{l}\displaystyle \lim_{x \to +\infty} (x^3-x^2+4)= (+\infty) ^3 = \bm{+\infty}\\[4ex]\displaystyle\lim_{x \to +\infty} (-5x+2)= -5(+\infty)= \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^2-7x+1) = (-\infty)^2 = \bm{+\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^3-x^2+4)= (-\infty) ^3 = \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to +\infty} \ \cfrac{1}{x}= \cfrac{1}{+\infty} = \bm{0}\end{array}$

Onbepaalde grenzen tot in het oneindige

De grenzen tot het oneindige zullen niet altijd zo eenvoudig te berekenen zijn, omdat we soms de onbepaaldheid van de oneindigheid tussen oneindigheid of de onbepaaldheid van oneindigheid minus oneindigheid zullen verkrijgen.

$\cfrac{\infty}{\infty}\qquad \qquad \infty-\infty$

Wanneer we dit soort onbepaalde vormen (of onbepaalde vormen) krijgen, kunnen we het resultaat niet direct weten, maar moeten we eerder een voorbereidende procedure uitvoeren om de grenswaarde te vinden. We zullen dan zien hoe de onbepaalde grenzen op oneindig worden opgelost.

Oneindige onbepaaldheid tussen het oneindige

Om het resultaat van onbepaaldheid oneindig gedeeld door oneindig te vinden, moeten we de graad van de teller en de graad van de noemer van de breuk vergelijken:

Als de graad van het tellerpolynoom kleiner is dan de graad van het noemerpolynoom, is de oneindige onbepaaldheid over oneindig gelijk aan nul.
Als de graad van het tellerpolynoom equivalent is aan de graad van het noemerpolynoom, is de oneindige onbepaaldheid over oneindig het quotiënt van de hoofdcoëfficiënten van de twee polynomen.
Als de graad van het tellerpolynoom groter is dan de graad van het noemerpolynoom, geeft de oneindige onbepaaldheid tussen oneindigheid min of meer oneindigheid (het teken hangt af van de hoofdtermen van de twee polynomen).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> In de volgende limiet is het tellerpolynoom bijvoorbeeld van de tweede graad, terwijl het noemerpolynoom van de derde graad is, dus de oplossing voor de limiet is 0. <p class=$ $\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

Kijk naar dit andere voorbeeld, waarin de twee polynomen van de rationale functie van de tweede graad zijn, dus we moeten de coëfficiënten van de termen van hogere graad delen om de limiet op oneindig te berekenen.

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

Ten slotte heeft de functie van de teller bij de volgende limiet een grotere graad dan die van de noemer, dus de onbepaaldheid van oneindigheid op oneindig geeft oneindigheid. Bovendien wordt een positieve oneindigheid verkregen uit de teller, maar een negatieve oneindigheid uit de noemer, dus het resultaat van de limiet is negatief (het positieve tussen het negatieve is negatief).

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Oneindige onbepaaldheid tussen oneindigheid met wortels

Aan de andere kant is de mate van een irrationele functie (functie met wortels) het quotiënt tussen de mate van de hoofdterm en de index van de radicaal.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

Als de limiet van een functie met wortels een oneindige onbepaaldheid tussen oneindig geeft , moeten we daarom dezelfde regels toepassen als hierboven uitgelegd met betrekking tot de graden van de teller en de noemer, maar er rekening mee houden dat de graad van een polynoom met wortels anders wordt berekend.

Kijk naar het volgende voorbeeld van de oneindige limiet van een functie met radicalen:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

De graad van de teller is 2 en de graad van de noemer is 4 (8/2=4), dus de limiet is 0 omdat de graad van de teller kleiner is dan de graad van de noemer.

Oneindige onbepaaldheid tussen oneindigheid met exponentiële functies

De groei van een exponentiële functie is veel groter dan de groei van een polynomiale functie, dus we moeten bedenken dat de graad van een exponentiële functie groter is dan de graad van een polynomiale functie.

$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”> Dus als de onbepaaldheid oneindig gedeeld door oneindig voortvloeit uit een limiet met exponentiële functies, moeten we eenvoudigweg dezelfde regels toepassen die de graden van de teller en de noemer verklaren, maar er rekening mee houden dat een exponentiële functie van een hogere orde is dan een polynoom. Bovendien, als we exponentiële functies hebben in de teller en de noemer van de deling, zal de exponentiële functie met de grootste basis die van de hoogste orde zijn. <p class=$ $\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

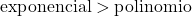
In dit voorbeeld wordt de noemer gevormd uit een exponentiële functie, dus deze is van hogere orde dan de teller. Daarom geeft de onbepaalde vorm oneindig tussen oneindigheid 0.

Oneindige minus oneindige onbepaaldheid

Het oplossen van de oneindige minus oneindige onbepaaldheid hangt af van het feit of de functie breuken of wortels heeft. Laten we dus eens kijken hoe we dit soort onbepaaldheid voor deze twee verschillende gevallen kunnen oplossen.

Onbepaaldheid oneindig min oneindig met breuken

Wanneer oneindig min oneindige onbepaaldheid optreedt bij het optellen of aftrekken van algebraïsche breuken , moeten we eerst de breuken optellen of aftrekken en vervolgens de limiet berekenen.

Laten we eens kijken hoe we de onbepaaldheid oneindig min oneindig kunnen berekenen in een functie met breuken door stap voor stap een voorbeeld op te lossen:

$\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)$

We proberen eerst de limiet te berekenen:

$\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}$

Maar we verkrijgen de onbepaaldheid ∞-∞.

We moeten eerst de breuken aftrekken. Om dit te doen, reduceren we breuken tot een gemeenschappelijke noemer, dat wil zeggen, we vermenigvuldigen de teller en de noemer van de ene breuk met de noemer van de andere:

$\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}$

En nu de twee breuken dezelfde noemer hebben, kunnen we ze combineren tot één breuk:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}$

We werken met de teller en de noemer:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}$

En tenslotte berekenen we de limiet opnieuw:

$\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}$

In dit geval geeft de oneindige onbepaaldheid tussen oneindigheid +∞ omdat de graad van de teller groter is dan de graad van de noemer.

Onbepaaldheid oneindig min oneindig met wortels

Wanneer oneindig min oneindige onbepaaldheid optreedt bij radicale optelling of aftrekking , moeten we eerst de functie vermenigvuldigen en delen door de geconjugeerde radicale uitdrukking en vervolgens de limiet oplossen.

Laten we eens kijken hoe we de onbepaaldheid oneindig min oneindig in een irrationele functie kunnen oplossen door een stapsgewijs voorbeeld te volgen:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)$

We proberen eerst de limiet van de functie op te lossen met radicalen:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}$

We verkrijgen echter de onbepaalde vorm ∞-∞. Dus om te weten hoeveel onbepaaldheid oneindig minus oneindig is, moet je de uitgelegde procedure toepassen.

Omdat de functie radicalen heeft, vermenigvuldigen en delen we de gehele functie door de geconjugeerde irrationele uitdrukking:

$\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}$

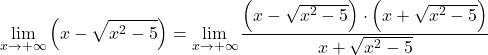
De algebraïsche uitdrukking van de teller komt overeen met de opmerkelijke identiteit van het product van een som en een verschil. Daarom kunnen we de uitdrukking vereenvoudigen:

$\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}$

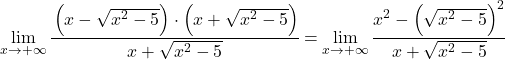
Nu vereenvoudigen we de wortel van de limiet, omdat deze in het kwadraat is:

$\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}$

We werken met de teller van de breuk:

$\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}$

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}$

En ten slotte voeren we de limietberekening opnieuw uit:

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}$

Het resultaat van de limiet is daarom 0, omdat elk getal gedeeld door oneindig gelijk is aan nul.

Opgeloste oefeningen over limieten op oneindig

Oefening 1

Zoek de volgende limieten van de grafiekfunctie:

$\displaystyle\lim_{x\to -\infty}f(x)$

$\displaystyle\lim_{x\to +\infty}f(x)$

$\displaystyle\lim_{x\to -1^-}f(x)$

$\displaystyle\lim_{x\to -1^+}f(x)$

$\displaystyle\lim_{x\to 1^-}f(x)$

$\displaystyle\lim_{x\to 1^+}f(x)$

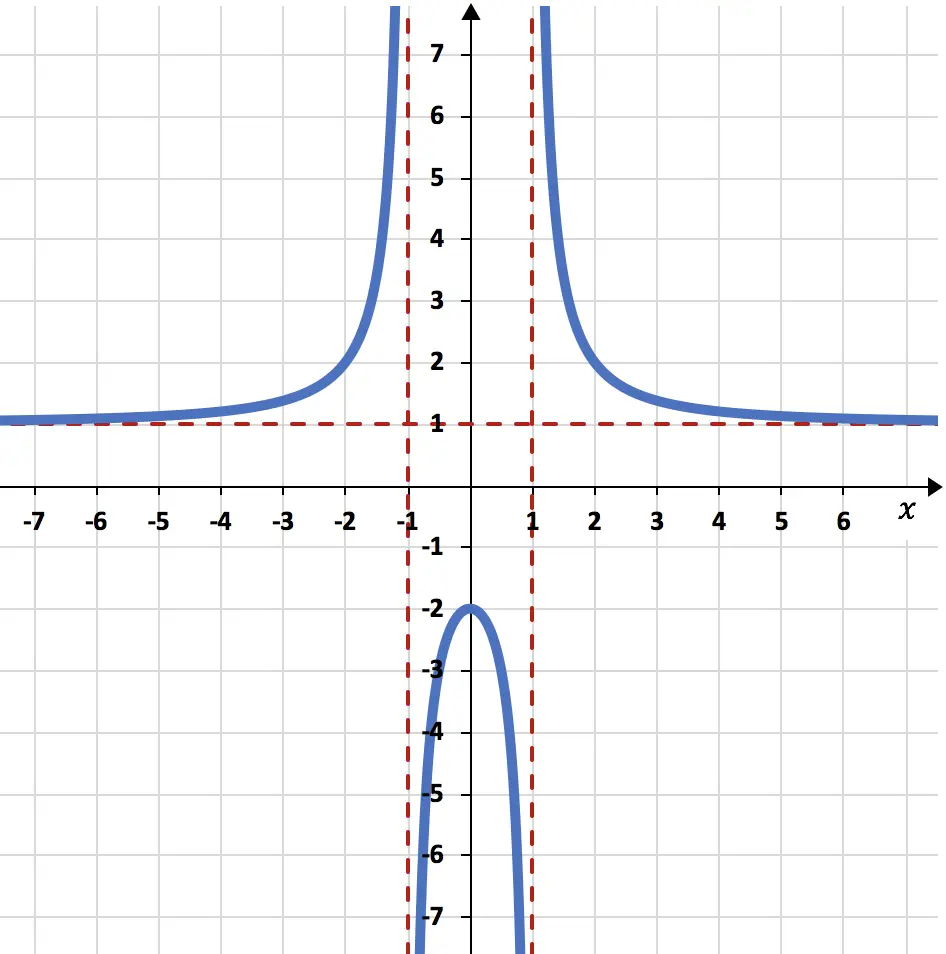
grenzen tot oneindig vanuit de representatie van een functie

Zie de oplossing

De limiet van de functie wanneer x neigt naar min oneindig en plus oneindig geeft 1:

$\displaystyle\lim_{x\to -\infty}f(x)=1$

$\displaystyle\lim_{x\to +\infty}f(x)=1$

De laterale grenzen van de functie links en rechts op het punt x=-1 zijn respectievelijk plus oneindig en minus oneindig:

$\displaystyle\lim_{x\to -1^-}f(x)=+\infty$

$\displaystyle\lim_{x\to -1^+}f(x)=-\infty$

Ten slotte zijn de laterale grenzen van de functie wanneer x naar 1 neigt, de moeite waard minus oneindig en plus oneindig:

$\displaystyle\lim_{x\to 1^-}f(x)=-\infty$

$\displaystyle\lim_{x\to 1^+}f(x)=+\infty$

Oefening 2

Los de limiet op naarmate x nadert plus oneindig van de volgende functie:

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1)$

Zie de oplossing

Om de limiet op oneindig op te lossen, moeten we x vervangen door oneindig in de term van de hoogste graad van de polynoom:

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1) = (+\infty)^2= \bm{+\infty}$

Oefening 3

Bereken de limiet tot oneindig van de volgende polynoomfunctie:

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5)$

Zie de oplossing

Om de limiet op oneindig op te lossen, vervangen we x door oneindig in de hoogste term van de polynoom en voeren we de berekeningen uit:

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5) = -3(+\infty)^2= -3\cdot (+\infty) = \bm{-\infty}$

Oefening 4

Los de ten minste oneindige limiet op van de volgende polynoomfunctie:

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4)$

Zie de oplossing

Om de limiet op oneindig te berekenen, vervangen we x door minus oneindig in de hoogste term van de polynoom en evalueren we de functie:

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4) = 6(-\infty)^2= 6\cdot (+\infty) = \bm{+\infty}$

Omdat minus oneindig wordt gekwadrateerd, wordt het teken van oneindigheid positief.

Oefening 5

Zoek de limiet op oneindig van de volgende rationale functie:

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5}$

Zie de oplossing

Om de limiet tot oneindig te bepalen, vervangen we x door plus oneindig op de term van de hoogste graad van de teller en noemer van de breuk:

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5} = \cfrac{7}{2\cdot(+\infty)}=\frac{7}{+\infty}=\bm{0}$

Onthoud dat elk getal gedeeld door plus of min oneindig gelijk is aan 0.

Oefening 6

Los de volgende limiet op oneindig op:

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x)$

Zie de oplossing

Om de limiet te berekenen wanneer x neigt naar ±∞ van een functie, kijk je eenvoudigweg naar de monomial van de hoogste graad van de functie:

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x) = -(-\infty)^3= -(-\infty)= \bm{+\infty}$

Oefening 7

Bereken de limiet van de volgende functie als x de negatieve oneindigheid nadert:

$\displaystyle \lim_{x \to -\infty} (-4x^2+4)$

Zie de oplossing

In dit geval is het voldoende om de kwadratische term te vervangen door oneindig:

$\displaystyle \lim_{x \to -\infty} (-4x^2+4) = -4(-\infty)^2= -4\cdot (+\infty) = \bm{-\infty}$

Oefening 8

Zoek de limiet van de volgende exponentiële functie als x oneindig nadert:

$\displaystyle \lim_{x \to +\infty} 2^x$

Zie de oplossing

Hoewel het een exponentiële functie is, is het proces om de limiet op te lossen hetzelfde: vervang x door oneindig.

$\displaystyle \lim_{x \to +\infty} 2^x = 2^{+\infty}=\bm{+\infty}$

Oefening 9

Los de oneindige limiet op van de volgende exponentiële functie:

$\displaystyle \lim_{x \to +\infty} 5^{-x}$

Zie de oplossing

Om deze limiet op te lossen, moet je de eigenschappen van breuken gebruiken:

$\displaystyle \lim_{x \to +\infty} 5^{-x} = 5^{-(+\infty)}=5^{-\infty}= \cfrac{1}{5^{+\infty}}= \cfrac{1}{\infty} =\bm{0}$

Oefening 10

Los de volgende limiet op oneindig op:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

Zie de oplossing

De limiet geeft onbepaaldheid minus oneindig tussen plus oneindig. De graad van de teller is groter dan de graad van de noemer, dus de onbepaalde limiet is gelijk aan plus oneindig. Omdat de deling echter negatief oneindig door positief oneindig is, is het resultaat negatief oneindig.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

Oefening 11

Corrigeer de volgende onbepaalde limiet:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

Zie de oplossing

In dit probleem wordt de onbepaalde vorm oneindig over oneindig verkregen uit het quotiënt van twee polynomen van dezelfde graad, dus het resultaat van de onbepaalde limiet is de verdeling van hun hoofdcoëfficiënten:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

Oefening 12

Bereken de volgende limiet minstens tot in het oneindige:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

Zie de oplossing

De mate van algebraïsche expressie van de teller is kleiner dan de mate van expressie van de noemer, dus de onbepaaldheid +∞/+∞ geeft 0:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

Oefening 13

Los de volgende onbepaalde limiet van een functie met wortels op:

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

Zie de oplossing

De uitdrukking van de teller staat onder een radicaal, de graad ervan is daarom 7/3. Aan de andere kant is het noemerpolynoom kwadratisch. En aangezien 7/3>2 geeft de limiet meer oneindigheid:

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=\bm{+\infty}$

Oefening 14

Bepaal de oneindige limiet van de volgende functie met breuken:

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

Zie de oplossing

In deze oefening verkrijgen we onbepaaldheid minus oneindig gedeeld door min oneindig, waarbij de graad van de teller groter is dan de graad van de noemer, dus:

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

Oefening 15

Zoek de ten minste oneindige limiet van de volgende functie:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

Zie de oplossing

Het noemerpolynoom is kwadratisch, terwijl het tellerpolynoom lineair is. Daarom geeft oneindige onbepaaldheid gedeeld door oneindig 0.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

Oefening 16

Los de ten minste oneindige limiet op van de volgende functie:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

Zie de oplossing

De teller is één graad groter dan de noemer, dus het resultaat van de onbepaalde vorm ∞/∞ zal oneindig zijn. Bovendien zal het oneindigheidsteken negatief zijn omdat positief tussen negatief zich vertaalt naar negatief:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Oefening 17

Los de volgende limiet op oneindig op:

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

Zie de oplossing

De exponentiële functie is van een hogere orde dan de polynomiale functie, dus de limiet geeft oneindigheid. Als u het positieve door het negatieve deelt, is het oneindigheidsteken echter negatief:

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

Oefening 18

Bereken de oneindige limiet van de volgende functie met een vierkantswortel:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}$

Zie de oplossing

De teller bestaat uit een vierkantswortel, de graad ervan is dus 2/2=1. Dan is de graad van de teller gelijk aan die van de noemer, dus de oneindige onbepaaldheid tussen oneindigheid wordt als volgt opgelost:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}= \cfrac{\sqrt{4(+\infty)^2}}{-2(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt{4}}{-2}=\cfrac{2}{-2}=\bm{-1}$

Oefening 19

Los de oneindige limiet van de volgende functie op met twee radicalen:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

Zie de oplossing

De graad van de teller is 7/3=2,33 en de graad van de noemer is 5/2=2,5. Daarom, aangezien de graad van de teller kleiner is dan de graad van de noemer, is de onbepaalde oneindige limiet tussen oneindigheid 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Oefening 20

Bereken de volgende limiet:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

Zie de oplossing

Ongeacht de graad van de teller, aangezien we een exponentiële functie in de noemer hebben, is het resultaat van de onbepaalde vorm oneindig over oneindig 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Oefening 21

Bepaal de oneindige limiet van de volgende rationale functie:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)$

Zie de oplossing

Eerst proberen we de limiet te berekenen door oneindig in de functie te vervangen:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}$

Maar we vinden de onbepaaldheid ∞ – ∞. Daarom herleiden we de breuken tot een gemeenschappelijke noemer:

$\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}$

En omdat de twee breuken nu dezelfde noemer hebben, kunnen we ze combineren tot één breuk:

$\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}$

We maken de haakjes van de teller:

$\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}$

En tenslotte bepalen we de limiet:

$\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}$

In dit geval geeft de onbepaaldheid ∞/∞ +∞ omdat de graad van de teller groter is dan de graad van de noemer.

Oefening 22

Los de limiet van de volgende fractionele functie op als x 0 nadert:

$\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)$

Zie de oplossing

We proberen eerst zoals gewoonlijk de limiet te berekenen:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}$

Maar we krijgen de onbepaalde vorm ∞-∞. We moeten daarom de fracties van de functie terugbrengen tot een gemeenschappelijke noemer.

In dit geval is x ⁴ een veelvoud van x ² , dus door simpelweg de teller en de noemer van de tweede breuk te vermenigvuldigen met x ² zorgen we ervoor dat beide breuken dezelfde noemer hebben:

$\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}$

We kunnen nu de twee breuken aftrekken:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}$

We proberen de limiet opnieuw op te lossen:

$\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}$

Maar we eindigen met de onbepaaldheid van een constante die begint bij nul. Het is daarom noodzakelijk om de laterale grenzen van de functie te berekenen.

$\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

$\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

Concluderend: aangezien de twee laterale grenzen van de functie op het punt x=0 -∞ opleveren, is de oplossing van de limiet -∞:

$\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}$

Oefening 23

Los de oneindige limiet van de volgende functie met wortels op:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)$

Zie de oplossing

Als we de limiet proberen op te lossen, krijgen we de onbepaaldheid oneindig min oneindig:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}$

Omdat er radicalen in de functie zitten, moet deze daarom worden vermenigvuldigd en gedeeld door de geconjugeerde radicaaluitdrukking:

$\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}$

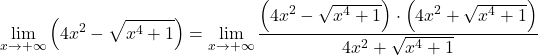
In de teller hebben we het opmerkelijke product van een som en een verschil, dat gelijk is aan het verschil van de kwadraten. Nog:

$\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}$

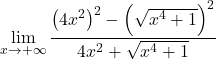
We vereenvoudigen de radicaal tot het kwadraat:

$\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}$

We werken met de teller:

$\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}$

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}$

En uiteindelijk vinden we de limiet:

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}$

In dit geval is de onbepaaldheid oneindig gedeeld door oneindig oneindiger omdat de graad van de teller groter is dan de graad van de noemer (bedenk dat de vierkantswortel de graad met twee reduceert:

$\sqrt{x^4} = x^{4/2} = x^2$

Oefening 24

Los de limiet op als x de oneindigheid nadert van de volgende irrationele functie:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)$

Zie de oplossing

Eerst proberen we de limiet zoals gewoonlijk te berekenen:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}$

Maar dit resulteert in de onbepaaldheid van het verschil van oneindigheden. Omdat de functie wortels heeft, moeten we de uitdrukking daarom vermenigvuldigen en delen door de geconjugeerde radicaal:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}$

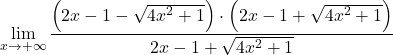
We groeperen de opmerkelijke gelijkheid van de teller van de breuk:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}$

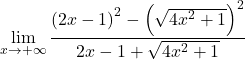
We lossen de vierkantswortel op:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

We lossen de opmerkelijke identiteit van het kwadraat van een verschil op:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

We werken met de teller:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}$

$\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}$

En tenslotte berekenen we de waarde van de limiet op oneindig:

$\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =$

Ook al staat er een x kwadraat in de noemer, de graad ervan is eigenlijk 1 omdat deze binnen een wortel staat:

$\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .$

Daarom is het resultaat van de onbepaaldheid -∞/+∞ de deling van de coëfficiënten van de x van de hoogste graad, aangezien de graad van de teller hetzelfde is als de graad van de noemer.

$\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}$

Merk op dat er twee eerstegraadstermen in de noemer staan

$\bigl(2x$

$\sqrt{4x^2}\bigr)$

, om de onbepaaldheid -∞/+∞ op te lossen is het noodzakelijk om alle coëfficiënten van de eerstegraadstermen te nemen, dat wil zeggen de

$2$

van

$2x$

en de

$\sqrt{4}$

van

$\sqrt{4x^2}.$

Oefening 25

Bereken de limiet als x 1 van de volgende functie met breuken benadert:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)$

Zie de oplossing

Door te proberen de limiet te maken, verkrijgen we de onbepaalde limiet van oneindig min oneindig:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}$

We moeten daarom de breuken herleiden tot een gemeenschappelijke noemer, of met andere woorden, we moeten de teller en de noemer van de ene breuk vermenigvuldigen met de noemer van de andere:

$\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}$

En omdat de twee breuken nu dezelfde noemer hebben, kunnen we ze samenvoegen:

$\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}$

Wij opereren:

$\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}$

$\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}$

En we proberen de limiet opnieuw op te lossen:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}$

Maar we vinden de onbepaaldheid nul gedeeld door nul. We moeten daarom de polynomen van de teller en de noemer ontbinden in factoren:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}$

Nu vereenvoudigen we de breuk door de factor te verwijderen die herhaald wordt in de teller en de noemer:

$\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}$

En ten slotte lossen we de limiet op:

$\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}$

Grenzen tot oneindig

Limiet van een functie wanneer x naar oneindig neigt

Hoe limieten op oneindig op te lossen

Voorbeelden van limieten tot oneindig

Onbepaalde grenzen tot in het oneindige

Oneindige onbepaaldheid tussen het oneindige

Oneindige onbepaaldheid tussen oneindigheid met wortels

Oneindige onbepaaldheid tussen oneindigheid met exponentiële functies

Oneindige minus oneindige onbepaaldheid

Onbepaaldheid oneindig min oneindig met breuken

Onbepaaldheid oneindig min oneindig met wortels

Opgeloste oefeningen over limieten op oneindig

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Oefening 6

Oefening 7

Oefening 8

Oefening 9

Oefening 10

Oefening 11

Oefening 12

Oefening 13

Oefening 14

Oefening 15

Oefening 16

Oefening 17

Oefening 18

Oefening 19

Oefening 20

Oefening 21

Oefening 22

Oefening 23

Oefening 24

Oefening 25

Laat een reactie achter Reactie annuleren