▷ Hoe alle soorten onbepaaldheid (limieten) op te lossen

In dit artikel leggen we uit wat onbepaaldheid is. Je ontdekt wat alle soorten onbepaaldheid zijn en hoe je deze kunt oplossen. Bovendien kun je stap voor stap opgeloste oefeningen zien over de functiegrenzen van alle onbepaaldheden.

Wat zijn onbepaaldheden?

Onbepaalde vormen, ook wel onbepaalde vormen genoemd, zijn wiskundige uitdrukkingen die voorkomen bij de berekening van de grenzen van functies waarvan het resultaat niet is gedefinieerd. Om de onbepaaldheid van de limieten op te lossen, is het dus noodzakelijk een voorbereidende procedure toe te passen die afhangt van het type functie.

Dat wil zeggen, wanneer we onbepaaldheid krijgen, betekent dit niet dat de limiet niet bestaat of dat deze niet kan worden opgelost, maar eerder dat we wijzigingen in de functie zullen moeten aanbrengen om de oplossing van de limiet te vinden.

Soorten onbepaaldheid

Onbepaalde vormen, of onbepaalde vormen, worden ingedeeld in de volgende typen:

Onbepaaldheid oneindig min oneindig (∞-∞)
Aantal onbepaaldheid tussen nul (k/∞)
Nul onbepaaldheid tussen nul (0/0)
Oneindige onbepaaldheid tussen oneindig (∞/∞)
Onbepaaldheid 1 verhoogd tot oneindig (1 ^∞ )
Nul onbepaaldheid verhoogd naar nul (0 ⁰ )
Nul onbepaaldheid voor oneindig (0·∞)
Nul onbepaaldheid verhoogd tot oneindig (0 ^∞ )
Oneindige onbepaaldheid op nul gebracht (∞ ⁰ )

We zullen dan zien hoe we alle soorten onbepaaldheid kunnen oplossen.

Oneindige minus oneindige onbepaaldheid

De onbepaalde vorm oneindig min oneindig is niet gelijk aan nul, omdat we twee zeer grote getallen aftrekken, maar we weten niet welke groter is. Het resultaat van het verschil in oneindigheden hangt daarom af van de orde van elke oneindigheid.

$\infty-\infty$

Het oplossen van dit soort onbepaaldheid is niet eenvoudig, omdat afhankelijk van het type functie de ene of de andere procedure moet worden toegepast. Daarom raden wij u aan de volledige uitleg in de volgende link te bekijken:

➤ Zie: hoe je de onbepaaldheid oneindig min oneindig oplost

Aantal onbepaaldheid tussen nul

De onbepaaldheid van een constante gedeeld door nul wordt verkregen wanneer de noemer van een rationale functie wordt geannuleerd.

$\cfrac{k}{0}$

Het resultaat van dit type onbepaalde vorm zal altijd oneindiger, minder oneindig zijn, anders zal de limiet van de functie niet bestaan. Laten we eens kijken hoe deze onbepaaldheid wordt berekend door als voorbeeld een limiet op te lossen:

$\displaystyle\lim_{x\to 0}\cfrac{-4}{x^2}=\cfrac{-4}{0^2}=\cfrac{-4}{0}=\infty$

We hebben de onbepaaldheid verkregen van een getal gedeeld door nul, dus we moeten de laterale grenzen van de functie berekenen:

$\displaystyle\lim_{x\to 0^-}\cfrac{-4}{0^2}=\cfrac{-4}{(-0,001)^2}=\cfrac{-4}{+0}=-\infty$

$\displaystyle\lim_{x\to 0^+}\cfrac{-4}{0^2}=\cfrac{-4}{0,001^2}=\cfrac{-4}{+0}=-\infty$

➤ Zie: wat zijn laterale grenzen?

De twee laterale grenzen van de functie geven hetzelfde resultaat, dus per definitie geeft de limiet van de functie wanneer x naar 0 neigt minus oneindig:

$\displaystyle\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)=-\infty \ \longrightarrow \ \lim_{x\to 0}f(x)=-\infty$

Merk op dat als de laterale limieten verschillende waarden hadden gegeven, de limiet van de functie op dit punt niet zou bestaan.

Nul tussen nul onbepaaldheid

De onbepaalde limiet nul gedeeld door nul is heel gebruikelijk en wordt verkregen in functies met breuken waarin de teller en de noemer elkaar opheffen.

$\cfrac{0}{0}$

Dit type onbepaalde limiet wordt afhankelijk van de functie anders opgelost. Als de functie bijvoorbeeld wortels heeft, moeten verschillende stappen worden uitgevoerd. U kunt de verschillende resoluties van dit soort onbepaaldheid bekijken in de volgende link:

➤ Zie: hoe je de nul-onbepaaldheid tussen nul oplost

Oneindige onbepaaldheid tussen het oneindige

Oneindige onbepaaldheid tussen oneindigheid komt meestal voor in de oneindige grenzen van functies met breuken. Hoewel onbepaaldheid het quotiënt is van twee oneindigheden, hoeft het resultaat niet noodzakelijkerwijs oneindig te zijn.

$\cfrac{\infty}{\infty}$

Dit type onbepaalde vorm wordt door vergelijking opgelost. Dat wil zeggen, de graad van de teller en de graad van de noemer worden waargenomen en, afhankelijk van welke groter is, is het limietresultaat het een of het ander. Via de volgende link kunt u alle cases bekijken:

➤ Zie: opgeloste oefeningen over oneindige grenzen tussen oneindig

Onbepaaldheid 1 verhoogd tot oneindig

Wiskundig gezien zou je kunnen denken dat 1 tot oneindig 1 oplevert, aangezien elke macht van 1 gelijk is aan 1. Deze term is echter onbepaald en daarom kan men het resultaat ervan niet zo gemakkelijk afleiden.

$1^{\infty}$

Dit type onbepaaldheid wordt berekend door de volgende formule toe te passen:

$\displaystyle\lim_{x\to+\infty}f(x)^{g(x)}=\lim_{x\to+\infty}e^{g(x)\cdot [f(x)-1]}$

De volgende limiet is bijvoorbeeld onbepaald omdat deze de kracht van oneindigheid geeft:

$\displaystyle\lim_{x\to+\infty}\left(1-\frac{1}{x}\right)^x=\left(1-\frac{1}{+\infty}\right)^{+\infty}=(1-0)^{+\infty}=1^{+\infty}$

We moeten daarom de formule gebruiken voor dit type onbepaaldheid:

$\displaystyle\lim_{x\to+\infty}e^{x\cdot\left[1-\frac{1}{x}-1\right]}=\lim_{x\to+\infty}e^{x\cdot\left[-\frac{1}{x}\right]}=\lim_{x\to+\infty}e^{-1}=\frac{1}{e}$

En zo hebben we de onbepaalde limiet, verhoogd naar het oneindige, al opgelost.

Nul onbepaaldheid naar nul gebracht

Nul-onbepaaldheid voor de nulmacht verschijnt binnen de grenzen van gecompliceerde functies.

$0^0$

Om dit type onbepaalde limiet op te lossen, moet u de volgende limit-eigenschap gebruiken:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

De volgende limiet geeft bijvoorbeeld de onbepaalde vorm 0 tot de macht 0:

$\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=\left(\frac{1}{+\infty}\right)^{\frac{1}{+\infty}}=0^0$

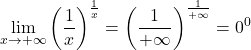
Maar als we logaritmen op de limiet toepassen, kunnen we de waarde ervan vinden:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln\left(\frac{1}{x}\right)}}=\\[5ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln\left(\frac{1}{x}\right)}{x}}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln1-\ln x}{x}}}=\\[5ex]=\displaystyle e^{^{\displaystyle\lim_{x\to +\infty}\frac{-\ln x}{x}}}=e^{^{\displaystyle\frac{-\infty}{+\infty}}}=e^0=1\end{array}$

Nul onbepaaldheid voor oneindigheid

Het is moeilijk om de onbepaaldheid van het product van nul en oneindig tegen te komen, maar dat betekent niet dat het gemakkelijk te bepalen is.

$0\cdot \infty$

Er bestaat niet één methode om dit soort onbepaaldheid op te lossen, maar deze is afhankelijk van het type functie. In dit geval moeten we de functie transformeren in oneindige onbepaaldheid gedeeld door oneindig of nul onbepaaldheid gedeeld door nul, en van daaruit de oplossingsmethoden toepassen die we hierboven voor elke onbepaaldheid hebben gezien.

Dus als de limiet van de ene functie 0 is en de limiet van de andere functie ∞:

$\displaystyle\lim_{x\to a}f(x)=0\qquad\lim_{x\to a}g(x)=\infty$

We kunnen dit type voor onbepaalde tijd transformeren door de volgende wijzigingen aan te brengen:

$\displaystyle\lim_{x\to a}f(x)\cdot g(x)\begin{cases}\displaystyle\lim_{x\to a}\frac{f(x)}{\displaystyle\frac{1}{g(x)}}=\frac{0}{0}\\[10ex]\displaystyle\lim_{x\to a}\frac{g(x)}{\displaystyle\frac{1}{f(x)}}=\frac{\infty}{\infty}\end{cases}$

Laten we eens kijken hoe we dit kunnen doen door als voorbeeld een onbepaalde limiet op te lossen:

$\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=e^{-\infty}\cdot (+\infty)=0\cdot \infty$

We werken met de functie om oneindige onbepaaldheid over oneindig te verkrijgen, en dan vinden we de limiet:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=\lim_{x\to +\infty}\frac{x}{\displaystyle\frac{1}{e^{-x}}}=\\[6ex]=\displaystyle \lim_{x\to +\infty}\frac{x}{e^x}=\frac{+\infty}{e^{+\infty}}=\frac{+\infty}{+\infty}=0\end{array}$

Nul onbepaaldheid verhoogd tot oneindig

De onbepaaldheid nul verhoogd tot oneindig is een beetje moeilijk te begrijpen, omdat we een heel klein getal naar een heel groot getal verheffen.

$0^{\infty}$

Wanneer deze onbepaalde vormen worden verkregen, moet de volgende formule worden gebruikt:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Laten we een voorbeeld oplossen om beter te begrijpen hoe u dit type onbepaaldheid kunt berekenen:

$\begin{array}{l}\displaystyle\lim_{x\to 0^+}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to 0^+}\frac{1}{x}\cdot \ln(x)}}=\\[3.5ex]\displaystyle =e^{^{\displaystyle\frac{1}{0^+}\cdot \ln(0^+)}}=e^{+\infty\cdot (-\infty)}\\[3ex]\displaystyle =e^{-\infty}=\frac{1}{e^{+\infty}}=0\end{array}$

Oneindige onbepaaldheid op nul gebracht

Normaal gesproken levert elke tot nul verheven macht 1 op, maar de onbepaaldheid van de oneindigheid tot nul hoeft niet noodzakelijk zo te zijn.

$\infty^0$

Net als bij de onbepaalde waarden nul verhoogd tot nul en nul verhoogd tot oneindig, is het voor het oplossen van dit type onbepaalde limiet noodzakelijk om logaritmen toe te passen:

$\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}$

Laten we eens kijken hoe dit soort onbepaalde limieten wordt opgelost door stap voor stap een voorbeeld te berekenen:

$\begin{array}{l}\displaystyle\lim_{x\to +\infty}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln(x)}}=\\[3ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln(x)}{x}}}=e^{^{\displaystyle\frac{\ln(+\infty)}{+\infty}}}=\\[3ex]\displaystyle =e^{^{\displaystyle\frac{+\infty}{+\infty}}}=e^0=1\end{array}$

Soorten onbepaalde grenzen (onbepaalde grenzen)

Wat zijn onbepaaldheden?

Soorten onbepaaldheid

Oneindige minus oneindige onbepaaldheid

Aantal onbepaaldheid tussen nul

Nul tussen nul onbepaaldheid

Oneindige onbepaaldheid tussen het oneindige

Onbepaaldheid 1 verhoogd tot oneindig

Nul onbepaaldheid naar nul gebracht

Nul onbepaaldheid voor oneindigheid

Nul onbepaaldheid verhoogd tot oneindig

Oneindige onbepaaldheid op nul gebracht

Laat een reactie achter Reactie annuleren