▷ Hoe de inverse of reciproque functie te vinden (opgeloste oefeningen)

In dit artikel leggen we uit wat een inverse (of reciproque) functie is en hoe je de inverse van een functie kunt berekenen. Je ontdekt ook hoe je gemakkelijk kunt weten of een functie een inverse heeft of niet, en wat de eigenschappen van dit soort functies zijn. Tenslotte kun je oefenen met stapsgewijze oefeningen op inverse functies.

Wat is de inverse functie?

De inverse functie, ook wel de reciproque functie genoemd, is de functie waarvan het domein het bereik is van een andere functie (de oorspronkelijke functie) en waarvan het bereik het domein is van de oorspronkelijke functie. De inverse functie van de functie f wordt uitgedrukt met het symbool f ^-1 .

Daarom is de inverse functie van f(x) de functie die aan de volgende voorwaarde voldoet:

Goud

$f^{-1}$

is de inverse functie van

$f.$

Het concept van een inverse functie kan ook worden gedefinieerd met behulp van functiesamenstelling, aangezien elke functie die is samengesteld met zijn inverse functie gelijk is aan de identiteitsfunctie:

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

➤ Zie: wat is functiesamenstelling?

Dus als aan de vorige vergelijking is voldaan, betekent dit dat

$f^{-1}$

is de inverse functie (of wederkerige functie) van

$f.$

Voorbeeld van inverse functie

Laten we, gegeven de definitie van inverse functie, een voorbeeld oplossen om de betekenis ervan beter te begrijpen.

Bepaal of de volgende functies inverse van elkaar zijn:

$f(x)=2x+1\qquad g(x)=\cfrac{x-1}{2}$

Als de twee functies het omgekeerde van elkaar zijn, wordt aan de volgende twee voorwaarden voldaan:

$(f \circ g)(x) = x \qquad \qquad (g \circ f)(x) = x$

Laten we dus controleren of aan beide vergelijkingen is voldaan. Wij controleren eerst

$(f \circ g)(x) = x:$

$\begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}$

➤ Als je de berekening die we zojuist hebben gemaakt niet begrijpt, ga dan naar de bovenstaande link voor Wat is de samenstelling van functies? , leggen we uit hoe je dit soort bewerkingen met functies kunt oplossen.

Zodat

$(f \circ g)(x) = x$

ja, het is gelukt. ✅

Laten we nu de gelijkheid controleren

$(g \circ f)(x) = x :$

$\begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}$

En de invertibiliteitsvoorwaarde

$(g \circ f)(x) = x$

het is ook gelukt. ✅

Concluderend: aangezien beide vergelijkingen gelden, zijn de twee functies inverse van elkaar.

Hieronder ziet u beide functies grafisch weergegeven. Merk op dat de grafieken van twee inverse functies symmetrisch zijn rond de bissectrice van het eerste en derde kwadrant:

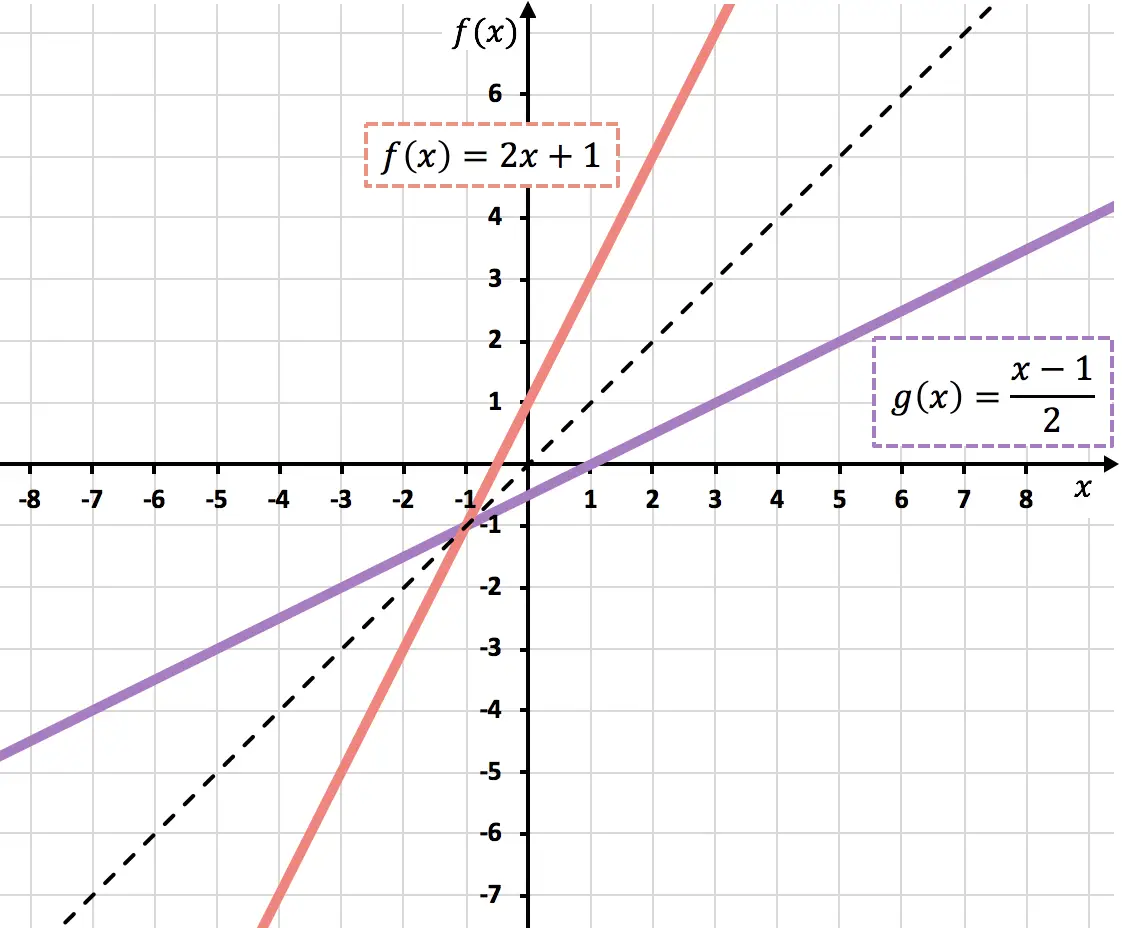
Hoe weet je of een functie een inverse heeft?

Een functie heeft een inverse functie als het een injectieve functie is , dat wil zeggen als elke waarde in zijn hele domein overeenkomt met een enkele waarde in zijn interval.

Exponentiële functie met inverse functie

Kwadratische functie zonder inverse functie

De linker exponentiële functie heeft bijvoorbeeld een inverse functie omdat elke x overeenkomt met een enkele waarde van f(x) . Aan de andere kant heeft de rechter kwadratische functie geen inverse functie, omdat deze verschillende waarden van x heeft waarvan de afbeeldingen gelijk zijn (bijvoorbeeld f(1)=f(3)=2) .

Op dezelfde manier bestaat een bijectieve functie uit een functie die zowel injectief als surjectief is, daarom heeft elke bijectieve functie ook een inverse functie.

Aan de andere kant moet je er rekening mee houden dat de inverse functie niet hetzelfde is als de multiplicatieve inverse van een functie , maar eerder twee verschillende concepten. Om de multiplicatieve inverse van een functie te vinden, berekent u eenvoudigweg 1 correspondentie met de genoemde functie.

$f^{-1}(x) \neq \cfrac{1}{f(x)}$

In de volgende sectie zullen we zien hoe we de inverse functie kunnen bepalen.

Hoe de inverse functie te vinden

Om de inverse van een functie te berekenen, moeten de volgende stappen worden uitgevoerd:

Vervang f(x) door y .
Verander alle x in y en omgekeerd.
Wis de y- variabele.
Vervang de variabele y door f ^-1 (x) . De inverse functie is de uitdrukking gevonden voor f ^-1 (x) .

Om precies te zien hoe de inverse functie wordt berekend, bepalen we als voorbeeld de inverse van de volgende functie:

$f(x) =4x+5$

Allereerst moeten we vervangen

$f(x)$

Voor

$y$

$y=4x+5$

Nu veranderen we alles

$x$

van de functie door

$y$

, en vice versa:

$y= 4x+5 \quad \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \quad x= 4y+5$

Vervolgens wissen we de variabele

$y:$

$x=4y+5$

$x-5=4y$

$\cfrac{x-5}{4}=y$

$y=\cfrac{x-5}{4}$

En tenslotte de inverse functie van

$f(x)$

is de algebraïsche uitdrukking die we hebben verkregen door te isoleren

$y:$

$\bm{f^{-1}(x) = } \cfrac{\bm{x-5}}{\bm{4}}$

Opgeloste oefeningen van de inverse functie

Hieronder hebben we verschillende stap-voor-stap oefeningen over de inverse functie voorbereid, zodat u kunt oefenen.

👉 Onthoud dat als je niet begrijpt hoe je een oefening moet oplossen of wilt dat wij een probleem voor je oplossen, je ons in de reacties kunt schrijven!

Oefening 1

Controleer of de volgende twee functies invers (of wederkerig) zijn of niet:

$f(x)=3x-7\qquad g(x)=\cfrac{x+7}{3}$

Zie de oplossing

Om de twee functies inverse van elkaar te laten zijn, moet het volgende waar zijn:

$(f \circ g)(x)=x \qquad \qquad (g \circ f)(x)=x$

Het is daarom noodzakelijk om te controleren of aan deze twee voorwaarden is voldaan. Wij controleren eerst

$(f \circ g)(x)=x :$

$\begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}$

Nog,

$(f \circ g)(x) = x$

ja, het is gelukt. ✅

Laten we nu de andere samenstelling van functies bekijken

$(g \circ f)(x)=x :$

$\begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}$

Waardoor

$(g \circ f)(x) = x$

het is ook gelukt. ✅

Hoe komt dat

$(f \circ g)(x)=x$

$(g \circ f)(x)=x$

, de twee functies zijn het omgekeerde van elkaar.

Oefening 2

Bereken de inverse (of reciproque functie) van de volgende polynoomfunctie van de eerste graad:

$f(x)=-2x-3$

Zie de oplossing

Het eerste dat u moet doen om de functie om te keren, is door de term te vervangen

$f(x)$

Voor

$}y:$

$y=-2x-3$

Nu veranderen we de

$x$

door

$y$

, en vice versa:

$y=-2x-3 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =-2y-3$

En dan laten wij los

$y:$

$x =-2y-3$

$x +3=-2y$

$\cfrac{x +3}{-2}=y$

$y = \cfrac{x +3}{-2}$

Het is ons al gelukt om vrij te geven

$y$

. Daarom is de inverse functie van

$f(x)$

Oosten:

$\bm{f^{-1}(x) = -} \cfrac{\bm{x+3}}{\bm{2}}$

Oefening 3

Inverteer de volgende kwadratische polynoomfunctie:

$f(x)=x^2-1$

Zie de oplossing

Om de inverse functie te vinden, zullen we de procedure volgen die we hierboven hebben gezien. Dus we zullen bellen

$y$

naar de functie

$f(x):$

$y=x^2-1$

Ten tweede passen we de

$x$

voor de

$y$

, en vice versa:

$y=x^2-1 \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x =y^2-1$

En ten slotte isoleren we de variabele

$y:$

$x =y^2-1$

$x+1=y^2$

$\sqrt{x+1}=y$

$y=\pm \sqrt{x+1}$

In dit geval heeft de verkregen functie echter twee afbeeldingen voor elk element van zijn domein (het positieve beeld en het negatieve beeld). Er is dus geen inverse functie van de probleemfunctie.

Oefening 4

Bepaal de inverse functie (of reciproque functie) van de volgende rationale functie:

$\displaystyle f(x)=\frac{x-1}{2x+3}$

Zie de oplossing

Eerst vervangen wij

$f(x)$

Voor

$y:$

$y=\cfrac{x-1}{2x+3}$

Nu veranderen we de

$x$

teller en noemer

$y$

, en vice versa:

$y=\cfrac{x-1}{2x+3} \ \xrightarrow{x \ \rightarrow \ y \ ; \ y \ \rightarrow \ x} \ x=\cfrac{y-1}{2y+3}$

En dan laten wij los

$y:$

$x=\cfrac{y-1}{2y+3}$

De uitdrukking

$2y +3$

deelt de hele rechterkant van de vergelijking, dus we kunnen deze vermenigvuldigen door de hele linkerkant van de vergelijking te vermenigvuldigen:

$x\cdot (2y+3)=y-1$

$2yx+3x=y-1$

Wij stellen alle voorwaarden aan

$y$

aan de ene kant van de vergelijking, en de andere termen aan de andere kant:

$2yx-y=-3x-1$

Om op te helderen

$}y$

, halen we de gemeenschappelijke factor uit de linkerkant van de vergelijking:

$y(2x-1)=-3x-1$

En als postbode

$(2x-1)$

is om de hele linkerkant van de vergelijking te vermenigvuldigen, we kunnen dit doen door de hele rechterkant te delen:

$y=\cfrac{-3x-1}{2x-1}$

Het is ons al gelukt om vrij te geven

$y$

. Dus de inverse functie van

$f(x)$

Oosten:

$\bm{f^{-1}(x)=} \cfrac{\bm{-3x-1}}{\bm{2x-1}}$

Eigenschappen van de inverse functie

De inverse functie heeft de volgende kenmerken:

De inverse functie is uniek, dat wil zeggen: als een functie inverteerbaar is, is er voor deze functie slechts één inverse functie.

Het domein van de inverse functie is het bereik (of bereik) van de oorspronkelijke functie.

Op dezelfde manier is het pad van de inverse functie equivalent aan het domein van de oorspronkelijke functie.

Elke functie die uit zijn inverse functie bestaat, geeft de identiteitsfunctie (x).

$(f\circ f^{-1})(x)=(f^{-1}\circ f)(x)=x$

De grafiek van een functie en de grafiek van zijn inverse functie zijn symmetrisch rond de bissectrice van het eerste en derde kwadrant.

De inverse van de inverse functie is gelijk aan de oorspronkelijke functie:

$\left(f^{-1}\right)^{-1}=f$

Het omkeren van een samengestelde functie komt overeen met het afzonderlijk berekenen van de inverse van elke functie en het vervolgens samenstellen van de inverse functies.

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

Een functie is tegelijkertijd continu met zijn inverse functie, of met andere woorden: als een functie continu is, zal zijn inverse functie dat ook zijn.

Als een functie differentieerbaar is en de afgeleide op geen enkel moment verdwijnt
$f'(x)\neq 0$

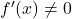
, zal de inverse functie ervan ook differentieerbaar zijn.

Bovendien kan de afgeleide van de inverse functie worden berekend door de inverse functiestelling toe te passen, waarvan de formule is:

$\left(f^{-1}\right)'(y)=\cfrac{1}{f'(x)}$

Inverse (of wederzijdse) functie

Wat is de inverse functie?

Voorbeeld van inverse functie

Hoe weet je of een functie een inverse heeft?

Hoe de inverse functie te vinden

Opgeloste oefeningen van de inverse functie

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Eigenschappen van de inverse functie

Laat een reactie achter Reactie annuleren