▷ Samenstelling van functies (of samengestelde functie)

In dit artikel leggen we uit wat de samengestelde functie (of samenstelling van functies) is. Bovendien kunt u verschillende voorbeelden zien van samengestelde functies en hoe het domein van dit soort functies wordt berekend. Tenslotte vind je de eigenschappen van functiesamenstelling en een aantal stap-voor-stap oefeningen om te oefenen.

Wat is functiesamenstelling?

Functiesamenstelling bestaat uit het achtereenvolgens evalueren van dezelfde waarde van de onafhankelijke variabele (x) in twee of meer functies. Als u bijvoorbeeld de functies (gof)(x) samenstelt, ontstaat de samengestelde functie g[f(x)].

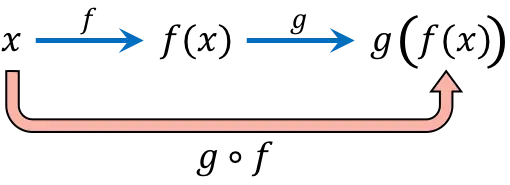
De uitdrukking van de samengestelde functie

$g\circ f$

we lezen “f samengesteld met g” of “f gevolgd door g”.

Houd er rekening mee dat de volgorde belangrijk is bij het samenstellen van functies; de functie rechts van het compositiesymbool wordt als eerste toegepast

$(f)$

dan de functie links van het compositiesymbool

$(g).$

Voorbeeld van functiesamenstelling

Laten we, gegeven de definitie van een samengestelde functie, een voorbeeld bekijken van hoe de samenstelling van twee functies kan worden berekend.

Gegeven de volgende twee verschillende functies:

$f(x)=3x+1 \qquad g(x)=\cfrac{x+4}{2}$

Bereken de samengestelde functie

$\left(g \circ f\right)(x)$

en evalueer het daarin

$x=3.$

De samenstelling van functies

$\left(g \circ f\right)(x)$

Dit betekent dat we de volgende samengestelde functie moeten uitvoeren:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Om het op te lossen, vervangen we

$f(x)$

door zijn algebraïsche uitdrukking:

$g\Big(f(x)\Big)= g\Big(3x+1\Big)$

En nu nemen we de functie van

$g(x)=\cfrac{x+4}{2}$

en we plaatsen de uitdrukking

$3x+1$

waar er een is

$x:$

$g\Big(3x+1\Big)=\cfrac{(3x+1)+4}{2}=\cfrac{3x+5}{2}$

Op deze manier hebben we al de functie f berekend die bestaat uit g :

$\left(g \circ f\right)(x)=\cfrac{3x+5}{2}$

Tenslotte, om de samengestelde functie in te evalueren

$x=3$

Bereken eenvoudig het beeld van de functie in de genoemde waarde:

$\left(g \circ f\right)(3)=\cfrac{3\cdot 3+5}{2}=\cfrac{14}{2}=7$

Samengesteld functiedomein

Wanneer we bewerkingen op functies uitvoeren, is het domein van de resulterende functie normaal gesproken het snijpunt van de domeinen van de oorspronkelijke functies. Aan deze eigenschap wordt echter niet voldaan door de functiesamenstelling.

Het domein van functiesamenstelling

$(g\circ f)(x)$

is equivalent aan de verzameling van alle waarden van x in het domein van de functie

$f$

zoals

$f(x)$

behoort tot het domein van de functie

$g.$

$\text{Dom}(g\circ f)=\{x\in\text{Dom}(f)\ | \ f(x)\in \text{Dom}(g)\}$

Om het domein van een samengestelde functie te berekenen, moet u daarom eerst het domein van elke functie afzonderlijk vinden, en vervolgens het domein van de functie die het resultaat is van de bewerking. Het domein van de samenstelling van de functies zal dus bestaan uit alle waarden die aan de vorige wiskundige voorwaarde voldoen.

👉 Onthoud: als je een probleem tegenkomt waarvan je niet weet hoe je het moet oplossen, kun je het ons vragen in de reacties hieronder!

Eigenschappen van functiesamenstelling

Samengestelde functies hebben de volgende kenmerken:

De samenstelling van functies heeft de associatieve eigenschap, daarom is de volgende vergelijking altijd waar:

$f\circ (g\circ h)=(f\circ g)\circ h$

Over het algemeen is de functiesamenstelling niet commutatief, dus de volgorde van de bewerking bepaalt het resultaat:

$f\circ g\neq g\circ f$

Het neutrale element van de samenstelling van functies komt overeen met de identiteitsfunctie
$f(x)=x.$

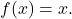
Elke functie die is samengesteld met de identiteitsfunctie resulteert dus in de functie zelf:

$f\circ id = id \circ f = f$

$id = x$

Het berekenen van de inverse van de samenstelling van twee functies komt neer op het eerst vinden van de inverse van elke functie en vervolgens het bepalen van de samengestelde functie:

$(f\circ g)^{-1}=f^{-1}\circ g^{-1}$

De inverse functie fungeert ook als een symmetrisch element van de samengestelde functie, aangezien de samenstelling van een functie met zijn inverse equivalent is aan de identiteitsfunctie:

$(f\circ f^{-1})^{-1}=(f^{-1}\circ f)=id=x$

De afgeleide van de samenstelling van twee functies wordt berekend met behulp van de kettingregel:

$\bigl(g\circ f\bigr)'(x)=g'\Bigl(f(x)\Bigr)\cdot f'(x)$

➤ Zie: wat is de kettingregel?

Opgeloste oefeningen over de samenstelling van functies

Oefening 1

Gegeven de volgende twee functies:

$f(x)=x-2 \qquad g(x)= 5x + 4$

Bereken de samenstellingen van de functies f samengesteld met g en g samengesteld met f .

$(g\circ f)(x)$

$(f\circ g)(x)$

Zie de oplossing

De samenstelling van functies

$\left(g \circ f\right)(x)$

betekent om de volgende samengestelde functie te berekenen:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

Dus om het op te lossen, vervangen we

$f(x)$

vanwege zijn uitdrukking:

$f(x)=x-2$

$g\Big(f(x)\Big)= g\Big(x-2\Big)$

$g\Big(x-2\Big)$

Dit betekent dat in de uitdrukking van

$g(x) =5x+4$

je moet de variabele vervangen

$x$

Voor

$x-2:$

$g\Big(x-2\Big) = 5(x-2) +4= 5x-10+4 = 5x-6$

Nog:

$\bm{\left(g \circ f\right)(x) = 5x-6}$

Aan de andere kant, om de functie g te vinden die uit f bestaat, moet je dezelfde procedure uitvoeren, maar dan in de omgekeerde volgorde:

$\begin{aligned}\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&=f\Big(5x+4\Big)\\[2ex]&=(5x+4)-2\\[2ex]&=\bm{5x+2}\end{aligned}$

Deze oefening demonstreert ook de eigenschap dat samengestelde functies niet commutatief zijn, omdat het resultaat afhangt van de volgorde waarin de functies worden toegepast.

Oefening 2

Gegeven de volgende twee functies:

$\displaystyle f(x) =x^2-3 \qquad g(x)=\frac{2x+3}{x+4}$

Berekent de samenstelling van functies f samengesteld uit g .

$(g\circ f)(x)$

Zie de oplossing

De functie f samengesteld uit g betekent het oplossen van de volgende samengestelde functie:

$\left(g \circ f\right)(x) = g\Big(f(x)\Big)$

We vervangen daarom de functie f(x) door zijn uitdrukking:

$g\Big(f(x)\Big)= g\Big(x^2-3 \Big)$

En nu moeten we vervangen

$x$

Voor

$x^2-3$

in de uitdrukking van de functie g(x):

$\begin{aligned}g\Big(x^2-3\Big)&=\cfrac{2(x^2-3)+3}{(x^2-3)+4}\\[2ex]&=\cfrac{2x^2-6+3}{x^2+1}\\[2ex]&=\cfrac{2x^2-3}{x^2+1}\end{aligned}$

Kort gezegd is het resultaat van de functiesamenstelling:

$\bm{\left(g \circ f\right)(x) =} \cfrac{\bm{2x^2-3}}{\bm{x^2+1}}$

Oefening 3

Gegeven de volgende twee kwadratische functies:

$\displaystyle f(x) =x^2 \qquad g(x)=g(x)= x^2-4x+8$

Bepaal het resultaat van de volgende samenstelling van functies:

$(g\circ f)(2)$

Zie de oplossing

$\left(g \circ f\right)(2)$

bestaat uit het vinden van de volgende samengestelde functie:

$\left(g \circ f\right)(2) = g\Big(f(2)\Big)$

Dus om de samengestelde functie op te lossen, berekenen we eerst

$f(2) :$

$f(x)=x^2$

$f(2)=2^2=4$

Daarom, als

$f(2)=4 :$

$\left(g \circ f\right)(2) = g\Big(f(2)\Big) = g\big(4\big)$

Om de waarde van de samengestelde functie te vinden, hoeft u dus alleen maar te berekenen

$g(4) :$

$\begin{aligned}\left(g \circ f\right)(2)&=g\Big(f(2)\Big)\\[2ex]&= g\big(4\big)\\[2ex]&=4^2-4\cdot 4+8 \\[2ex]&= 16 - 16 + 8\\[2ex]&= 8\end{aligned}$

Samenvattend is het resultaat van het functiecompositieprobleem:

$\bm{\left(g \circ f\right)(2) =8}$

Oefening 4

Gegeven de volgende twee functies:

$\displaystyle f(x)=\frac{2x-2}{-x+7}\qquad g(x)= x^2-1$

Zoek het resultaat van g samengesteld met f bij x=2:

$(f\circ g)(2)$

Zie de oplossing

In dit geval moeten we de volgende samengestelde functie berekenen:

$\left(f \circ g\right)(2) = f\Big(g(2)\Big)$

Dus eerst vinden we

$g(2) :$

$g(x)=x^2-1$

$g(2)=2^2-1=4-1 = 3$

En dus, zoals

$g(2)=3 :$

$\left(f \circ g\right)(2) = f\Big(g(2)\Big) = f\big(3\big)$

Om de samengestelde functie op te lossen, moeten we dus berekenen

$f(3) :$

$\begin{aligned}\left(f \circ g\right)(2)&=f\Big(g(2)\Big)\\[2ex]&= f\big(3\big)\\[2ex]&=\cfrac{2\cdot 3-2}{-3+7}\\[2ex]&=\cfrac{6-2}{-3+7}\\[2ex]&=\cfrac{4}{4}\\[2ex]&=1\end{aligned}$