Functietransformaties: vertaling, uitbreiding en symmetrie

Op deze pagina wordt uitgelegd wat functietransformaties zijn en hoe u ze kunt vinden. Er zijn drie soorten transformaties: translaties (of verplaatsingen), symmetrieën en expansies (of samentrekkingen). U vindt er ook oefeningen die stap voor stap zijn opgelost, zodat u de concepten zonder enige twijfel kunt oefenen en begrijpen.

Wat zijn functietransformaties?

Soms wordt ons gevraagd om elementaire functies in kaart te brengen die sterk lijken op andere functies die we al kennen. Welnu, in plaats van dezelfde functie opnieuw weer te geven, kunnen technieken worden gebruikt om gemakkelijk en snel over te schakelen van de weergave van de ene functie naar de andere.

Functietransformaties zijn dus technieken die het mogelijk maken om door middel van elementaire bewerkingen van de grafische weergave van een functie over te gaan naar de grafische weergave van een andere, zeer vergelijkbare functie.

In principe zijn er drie soorten transformaties van elementaire functies:

Vertalingen of bewegingen : een functie kan verticaal en horizontaal worden verplaatst.
Reflecties of symmetrieën : Een functie kan worden gereflecteerd met behulp van de X-as of de Y-as als symmetrieas.
Uitbreidingen en compressies : Een functie kan worden vergroot of verkleind.

Zodra we het concept van het transformeren van een functie zien, zullen we dieper ingaan op elk type wijziging.

Vertalingen of bewegingen van functies

We beginnen met functieverschuivingen. Er zijn twee soorten: verticale vertalingen en horizontale vertalingen.

Translatie of verticale beweging van een functie

Om een functie verticaal (langs de Y-as) te vertalen of te verplaatsen, moet u een constante aan de functie toevoegen of aftrekken:

We verplaatsen een functie k eenheden omhoog door ka toe te voegen aan de functie:

$\bm{f(x)+k}$

We verschuiven een functie k eenheden naar beneden door ka af te trekken van de functie:

$\bm{f(x)-k}$

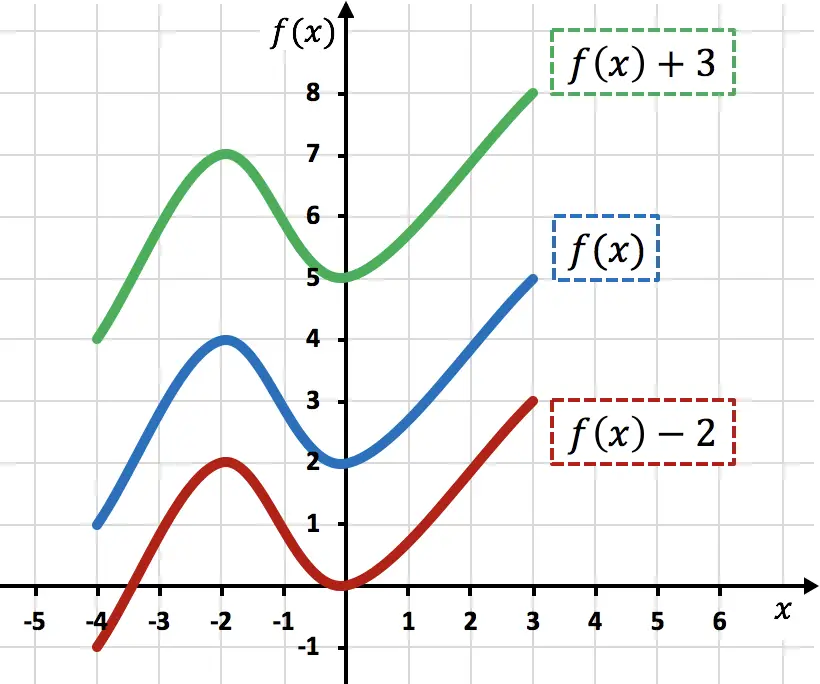
Translatie of verticale beweging van een functie

Zoals je in de grafiek kunt zien, verschuift het toevoegen van een constante aan een functie de toegevoegde eenheden naar boven (groene functie). Aan de andere kant, wanneer een getal van een functie wordt afgetrokken, worden de afgetrokken eenheden naar beneden verplaatst (rode functie).

Merk op dat bij dit type bewegingen alleen de Y-coördinaten van de functiepunten worden gewijzigd, terwijl de X-coördinaten hetzelfde blijven.

Vertaling of horizontale beweging van functies

Om een functie horizontaal (langs de X-as) te vertalen of te verschuiven, moet je een constante optellen of aftrekken van de onafhankelijke variabele x :

De grafiek van

$\bm{f(x+k)}$

is de grafiek van

$f(x)$

verplaatste k eenheden naar links.

De grafiek van

$\bm{f(x-k)}$

is de grafiek van

$f(x)$

verschoven k eenheden naar rechts.

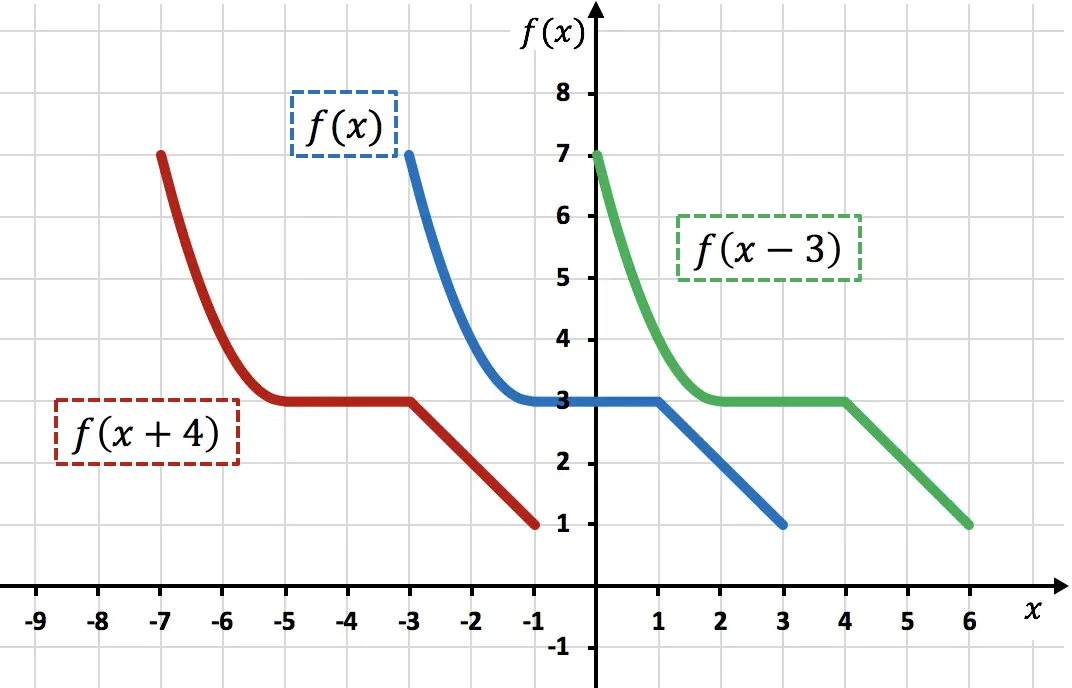
Translatie of horizontale beweging van een functie

Zoals u in de grafiek kunt zien, verschuift de functie, wanneer u een constante rechtstreeks aan de variabele x toevoegt, de toegevoegde eenheden naar links (rode functie). Aan de andere kant, wanneer een getal wordt afgetrokken van de variabele x , verschuift de functie de afgetrokken eenheden naar rechts (groene functie).

Merk op dat bij dit type bewegingen alleen de X-coördinaten van de functiepunten worden gewijzigd, terwijl de Y-coördinaten met dezelfde waarde doorgaan.

Voorbeeld van het vertalen of verplaatsen van een functie

Verplaats de volgende functie 4 eenheden naar boven en 3 eenheden naar rechts:

$f(x)=x^2$

Om de functie 4 eenheden omhoog te verplaatsen, moeten we 4 eenheden aan de functie toevoegen:

$f(x) + 4 = x^2 + 4$

En om de functie ook 3 eenheden naar rechts te verplaatsen, moeten we berekenen

$f(x-3)$

. Daarom, waar er een

$x$

we kunnen

$x-3 :$

$f(x-3) = (x-3)^2 + 4$

De functie 4 eenheden naar boven en 3 eenheden naar rechts verschoven is daarom:

$\bm{f(x) = (x-3)^2 + 4}$

Hieronder ziet u de oorspronkelijke functie en de getransformeerde functie in een grafiek weergegeven, zodat u het verschil ertussen kunt zien:

voorbeeld van vertaling of verplaatsing van een functie

Sommige wiskundigen noemen schuine verplaatsing of translatie wanneer beide soorten bewegingen tegelijkertijd plaatsvinden.

Reflectie of symmetrie van een functie ten opzichte van de coördinaatassen

We kunnen de symmetrische functie ten opzichte van elke cartesiaanse as op de volgende manier weergeven:

Om een functie weer te geven ten opzichte van de x-as, moeten we het teken van de functie veranderen, dat wil zeggen: we moeten berekenen

$\bm{-f(x)}.$

Om een functie weer te geven met betrekking tot de y-as, moeten we de onafhankelijke variabele x ontkennen, dat wil zeggen, we moeten berekenen

$\bm{f(-x)}.$

reflectie of symmetrie ten opzichte van de X-as

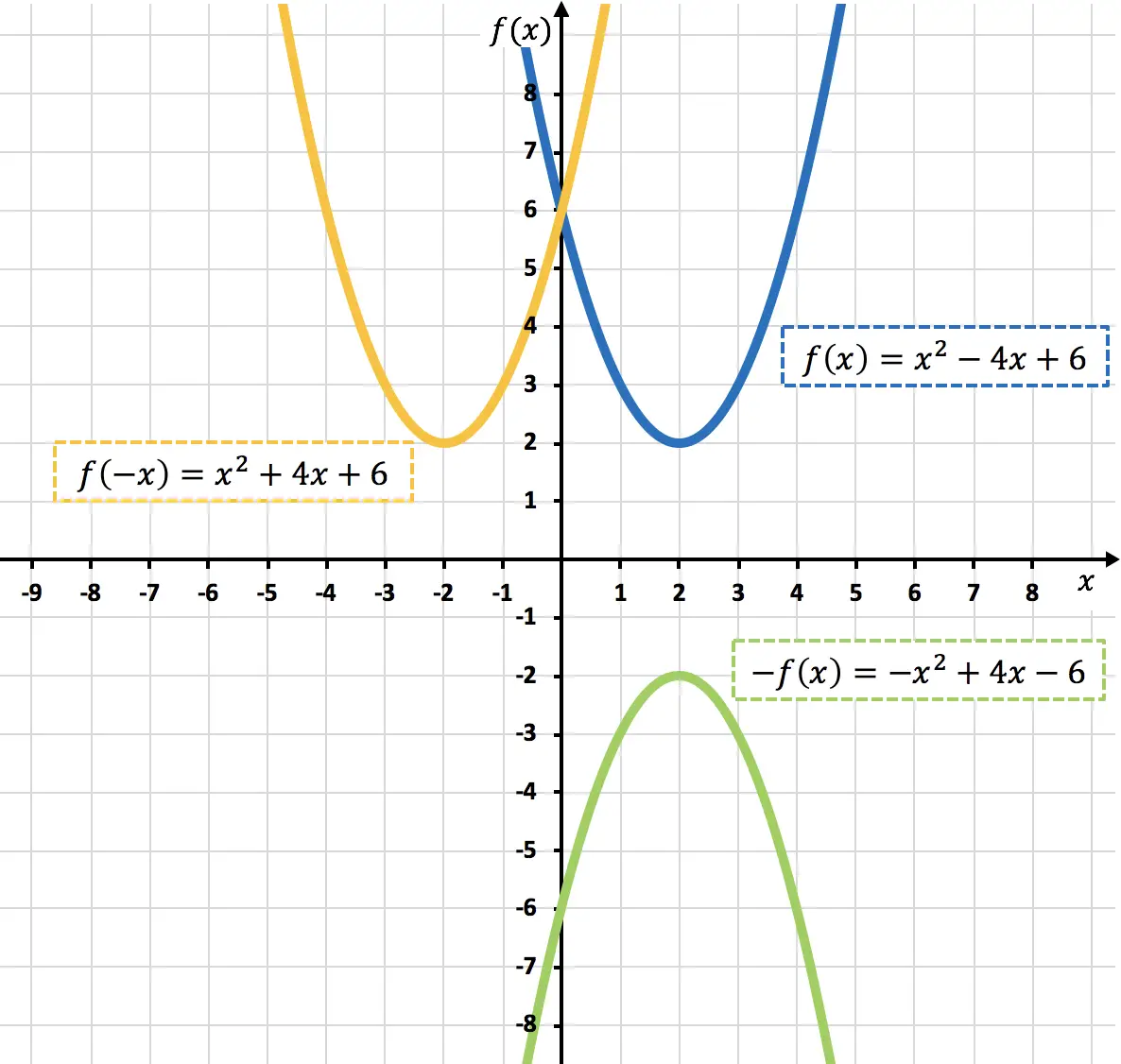
Zoals u in de vorige grafiek kunt zien, keren we, door een functie met -1 te vermenigvuldigen, deze grafisch om (oranje functie), of met andere woorden: we spiegelen deze ten opzichte van de X-as.

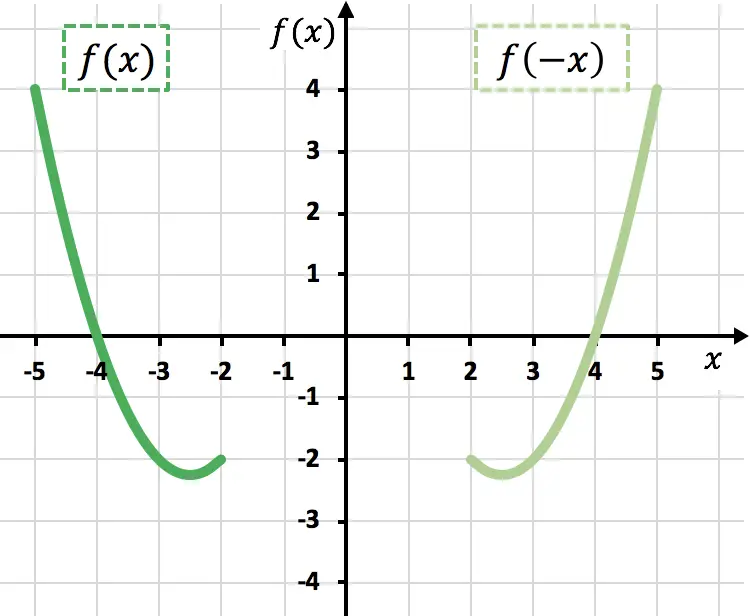
Zoals je in de vorige grafiek kunt zien, spiegelen we, door de variabele x te ontkennen, de functie ten opzichte van de Y-as (lichtgroene functie).

Voorbeeld van het spiegelen van een functie

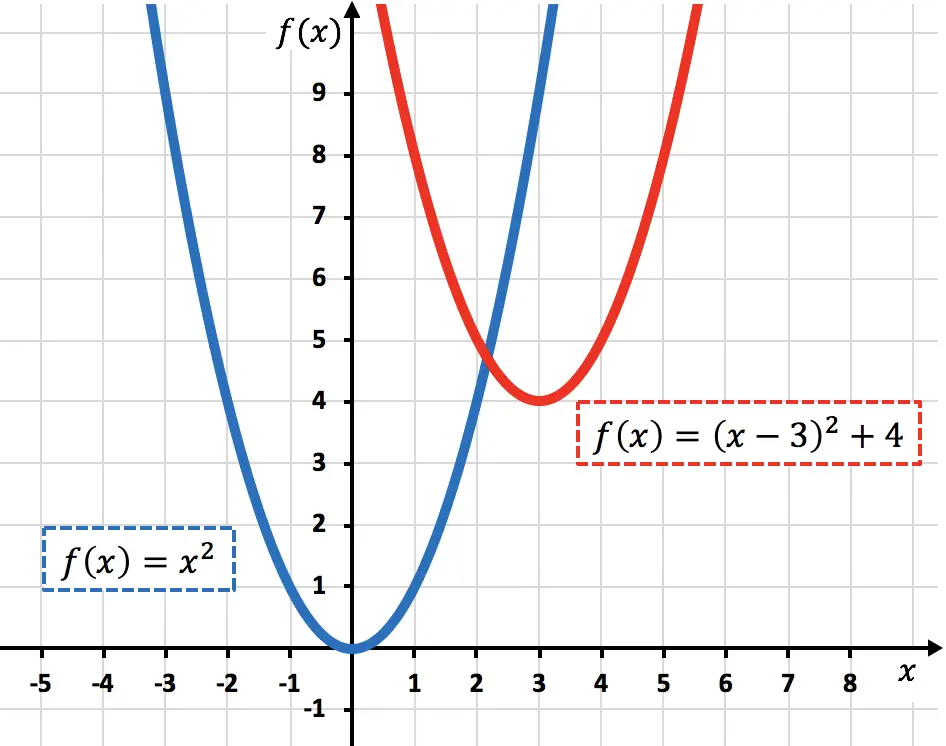
Bereken de symmetrische functie rond de OX-as en de symmetrische functie rond de OY-as van de volgende kwadratische functie:

$f(x)=x^2-4x+6$

Om de functie symmetrisch te vinden ten opzichte van de X-as, moeten we dit doen

$-f(x)$

$-f(x)=-\bigl[x^2-4x+6\bigr]$

$\bm{-f(x)=-x^2+4x-6}$

En om de functie symmetrisch te vinden ten opzichte van de Y-as moeten we doen

$f(-x)$

. Daarom vervangen we waar er een is

$x$

in de oorspronkelijke functie door de term

$-x :$

$f(x)=x^2-4x+6$

$f(-x)=(-x)^2-4\cdot (-x)+6$

$f(-x)=x^2-4\cdot (-x)+6$

$\bm{f(-x)=x^2+4x+6}$

Hieronder heb je zowel de originele functie als de gevonden symmetrische functies weergegeven:

voorbeeld van functies die symmetrisch zijn rond de x- en y-assen

Functie-uitbreidingen en -contracties

Net als bij vertalingen zijn er twee soorten uitzettingen of samentrekkingen: verticaal en horizontaal.

Verticale uitzetting en inkrimping van een functie

Door een geheel getalfunctie met een coëfficiënt te vermenigvuldigen, kunnen we deze laten uitzetten of inkrimpen:

Om een functie op de Y-as uit te breiden (of uit te breiden), moeten we deze vermenigvuldigen met een getal groter dan 1:

$kf(x)\qquad k>1″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”121″ style=”vertical-align: -5px;”></p> </p> <p style=$ Om een functie op de Y-as te verkleinen, moeten we deze vermenigvuldigen met een positief getal kleiner dan 1:

$kf(x)\qquad 0</div> <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="http://mathority.org/wp-content/uploads/2023/07/expansion-et-contraction-d-une-fonction.webp" alt="expansion et contraction verticales d'une fonction" class="wp-image-320" width="442" height="438" srcset="" sizes="" data-src=""></figure> </div> <p> Comme vous pouvez le voir dans le graphique précédent, si on multiplie une fonction par un coefficient supérieur à 1 (fonction verte) on la rend plus grande le long de l’axe OY, en revanche, si on multiplie une fonction par un coefficient supérieur à 0 mais plus petit que 1 (fonction rouge), nous le rendons plus petit le long de l’axe OY.</p> <h3 class="wp-block-heading"> Expansion et contraction horizontales d’une fonction</h3> <p> Dans ce cas, au lieu de multiplier la fonction entière par un coefficient, pour qu’une fonction se dilate ou se contracte horizontalement, nous devons multiplier la variable indépendante <em>x</em> . </p> <div style="padding-top: 23px; padding-bottom: 0.5px; padding-right: 30px; padding-left: 30px; border: 2px dashed #FF9B28; border-radius:20px;"> Pour <strong>étendre (ou dilater) une fonction sur l’axe X,</strong> il faut multiplier tous les <em>x</em> par un nombre compris entre 0 et 1 :” title=”Rendered by QuickLaTeX.com” height=”392″ width=”2425″ style=”vertical-align: -4px;”></p> <p> f(kx)\qquad 0</p> <p style=$ Om een functie op de X-as te verkleinen, moeten we alle x -en vermenigvuldigen met een getal groter dan 1:

$f(kx)\qquad k>1″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”121″ style=”vertical-align: -5px;”></p> </p> </div> <div class=$

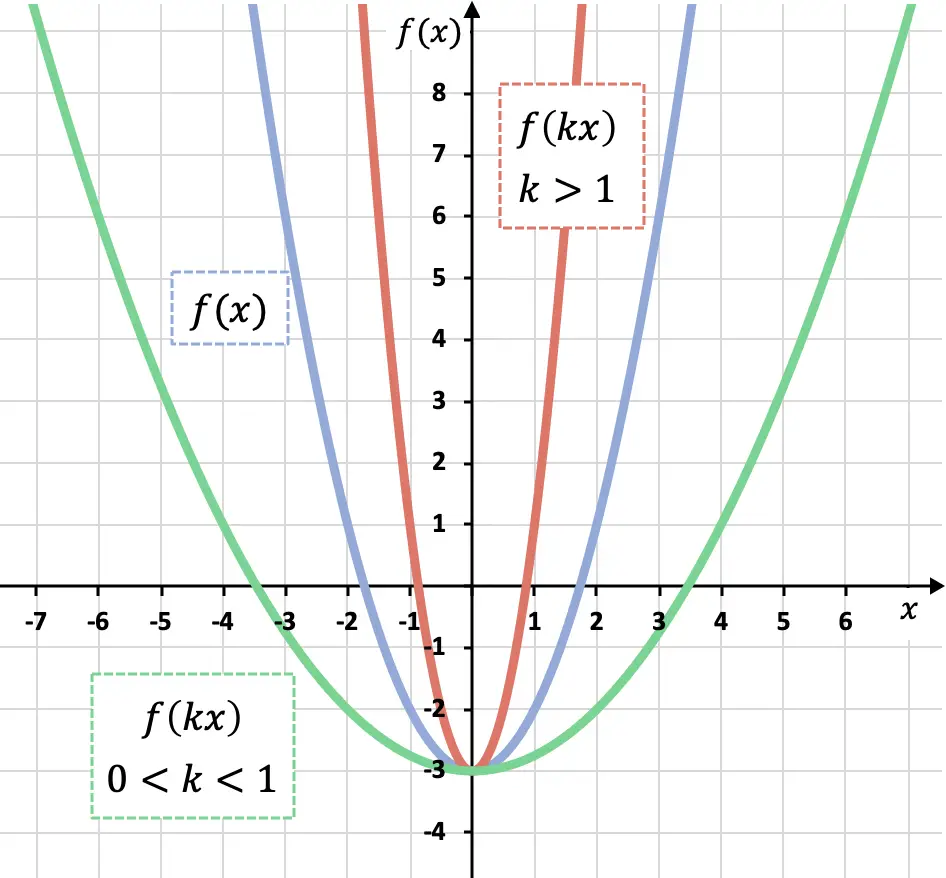
horizontale uitzetting of inkrimping van een functie

Zoals je in de vorige grafiek kunt zien, vergroten we deze langs de OX-as als we alle x -en van een functie vermenigvuldigen met een coëfficiënt groter dan 0 maar kleiner dan 1 (groene functie). een functie met een coëfficiënt groter dan 1 (rode functie) reduceren we deze langs de OX-as.

Voorbeeld van hoe u een functie kunt uit- of samenvouwen

Dupliceer de volgende irrationele functie verticaal en horizontaal:

$f(x)=\sqrt{9-x^2}$

Om de functie op de y-as met twee uit te breiden, moeten we de gehele functie met 2 vermenigvuldigen:

$2f(x)=2\sqrt{9-x^2}$

En om de functie ook met twee uit te breiden op de x-as, moeten we alle x -en van de functie vermenigvuldigen met

$\displaystyle \frac{1}{2}:$

$\displaystyle f\left(\frac{1}{2}x\right)=2\sqrt{9-\left(\frac{1}{2}x\right)^2}$

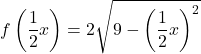
De functie die op de twee coördinaatassen wordt gedupliceerd, is daarom:

$\displaystyle\bm{f(x) = 2\sqrt{9-\left(\frac{1}{2}x\right)^2}}$

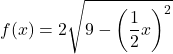
Hieronder ziet u de originele functie en de getransformeerde functie grafisch weergegeven, zodat u de verschillen ertussen kunt zien:

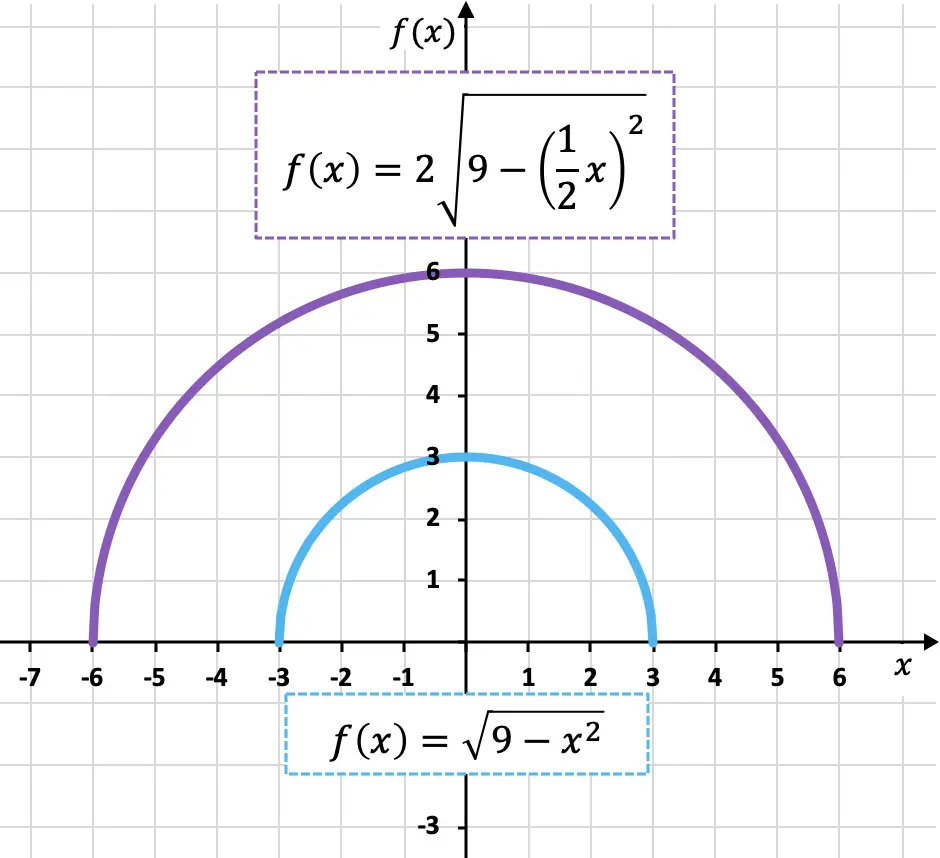
voorbeeld van hoe u een functie kunt uit- en samenvouwen

Zoals u kunt zien is het nieuwe object (paarse kleur) twee keer zo groot als het originele object (blauwe kleur), zowel verticaal als horizontaal. Daarom is het object uitgebreid.

Opgeloste oefeningen over functietransformaties

Oefening 1

Verplaats de volgende derdegraadsfunctie 5 eenheden omhoog:

$f(x) = 4x^3-9x-2$

Zie de oplossing

Om de functie 5 eenheden omhoog te verplaatsen, voegt u 5 toe aan de functie:

$\begin{aligned} f(x) + 5 & = 4x^3-9x-2 + 5 \\[2ex] & = 4x^3-9x+3 \end{aligned}$

De functie verschoven met 5 eenheden is daarom:

$\bm{f(x) = 4x^3-9x+3}$

Oefening 2

Zoek de symmetrische functie rond de Y-as van de volgende kwadratische functie:

$f(x) = 2x^2-3x+6$

Zie de oplossing

Om de functie symmetrisch ten opzichte van de Y-as te vinden, is het noodzakelijk om te berekenen

$f(-x)$

, dat wil zeggen, we moeten vervangen

$x$

Voor

$-x$

in de functie:

$f(-x) = 2(-x)^2-3\cdot (-x)+6$

$f(-x) = 2x^2+3x+6$

De symmetrische functie ten opzichte van de OY-as is daarom:

$\bm{f(x) = 2x^2+3x+6}$

Oefening 3

Voer een horizontale compressie uit van de volgende functie tot een derde van de weergave:

$f(x) = x^3-4x^2-5x+1$

Zie de oplossing

Om een functie te reduceren via de

$f(3x) = (3x)^3-4(3x)^2-5(3x)+1$

$f(3x) = 27x^3-4\cdot 9 x^2-15x+1$

$f(3x) = 27x^3-36 x^2-15x+1$

De gereduceerde functie is dus:

$\bm{f(x) = 27x^3-36 x^2-15x+1}$

Oefening 4

Bereken de symmetrische functie ten opzichte van de OX-as van de volgende functie, 4 eenheden naar rechts vertaald:

$f(x) = 3x^3-x^2+5x+8$

Zie de oplossing

Voordat we de symmetrische functie berekenen, moeten we de functie eerst 4 eenheden naar rechts verplaatsen, daarom:

$f(x-4) = 3(x-4)^3-(x-4)^2+5(x-4)+8$

$f(x-4) = 3(x-4)^3-(x-4)^2+5x-20+8$

$f(x-4) = 3(x-4)^3-(x-4)^2+5x-12$

En zodra we de functie hebben verplaatst, berekenen we de symmetrische functie ten opzichte van de X-as. Om dit te doen, moeten we de verkregen functie ontkennen:

$\displaystyle -f(x) = -\Bigl[3(x-4)^3-(x-4)^2+5x-12\Bigr]$

$-f(x) = -3(x-4)^3+(x-4)^2-5x+12$

Kort gezegd is de functie na toepassing van alle elementaire bewerkingen:

$\bm{f(x) =-3(x-4)^3+(x-4)^2-5x+12}$

Oefening 5

Verschuif de volgende functie 2 eenheden naar links en breid deze vervolgens verticaal uit met een factor 4:

$f(x) = x^4-5x^3-x-3$

Zie de oplossing

Eerst verplaatsen we de functie twee eenheden naar links:

$f(x+2) = (x+2)^4-5(x+2)^3-(x+2)-3$

$f(x-4) = (x+2)^4-5(x+2)^3-x-2-3$

$f(x-4) = (x+2)^4-5(x+2)^3-x-5$

En dan breiden we de functie uit langs de Y-as met een factor 4:

$4\cdot f(x) = 4\cdot \Bigl[(x+2)^4-5(x+2)^3-x-5\Bigr]$

$f(x) = 4(x+2)^4-20(x+2)^3-4x-20$

Concluderend is de functie na toepassing van alle elementaire transformaties:

$\bm{f(x) =4(x+2)^4-20(x+2)^3-4x-20}$

Oefening 6

Van de functie

$f(x)=x,$

Bepaal welke van de representaties in de grafiek overeenkomt met de functie

$f(x)=x-3 .$

Zie de oplossing

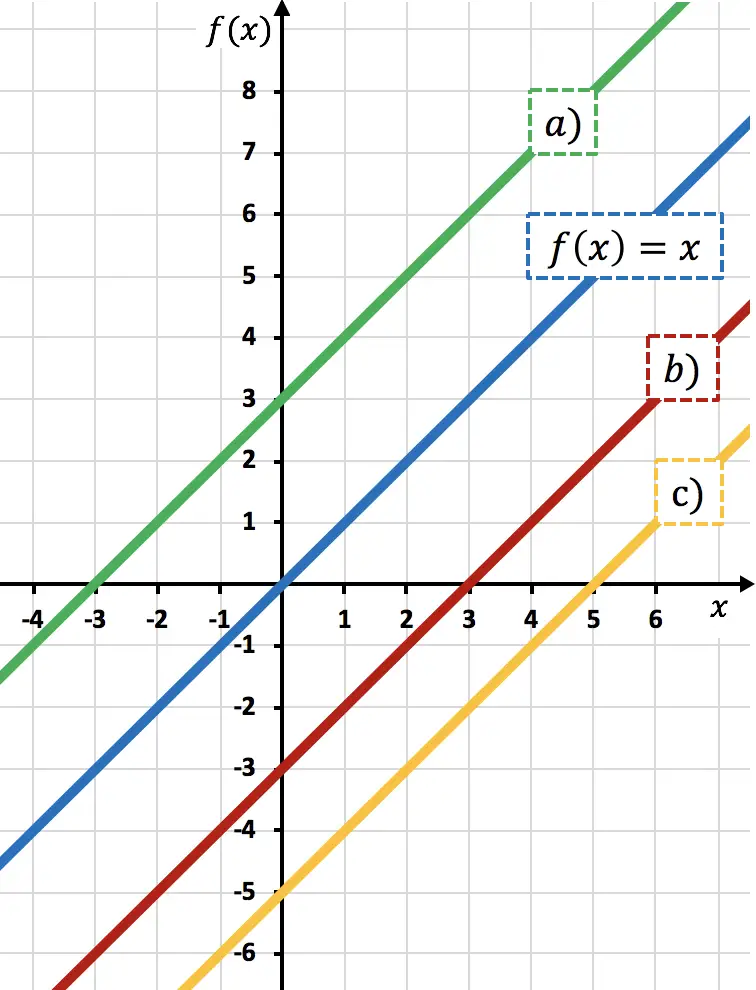
Functie

$f(x)=x-3$

is de functie

$f(x)=x$

3 eenheden naar beneden verplaatst. Want door een getal van een functie af te trekken, verplaats je de functie naar beneden.

Daarom is de vertegenwoordiging van

$f(x)=x-3$

komt overeen met de lijn b) , omdat deze 3 eenheden naar beneden is verschoven ten opzichte van

$f(x)=x .$

Dit kun je zien door naar de verticale as te kijken: wanneer

$f(x)=x$

gaat door 0, de rode lijn gaat door -3, dus deze wordt 3 eenheden naar beneden verschoven.

Oefening 7

Van de functie

$f(x)=x^2+2,$

Bepaal welke parabool de representatie is van de functie

$f(x)=(x-6)^2+2 .$

Zie de oplossing

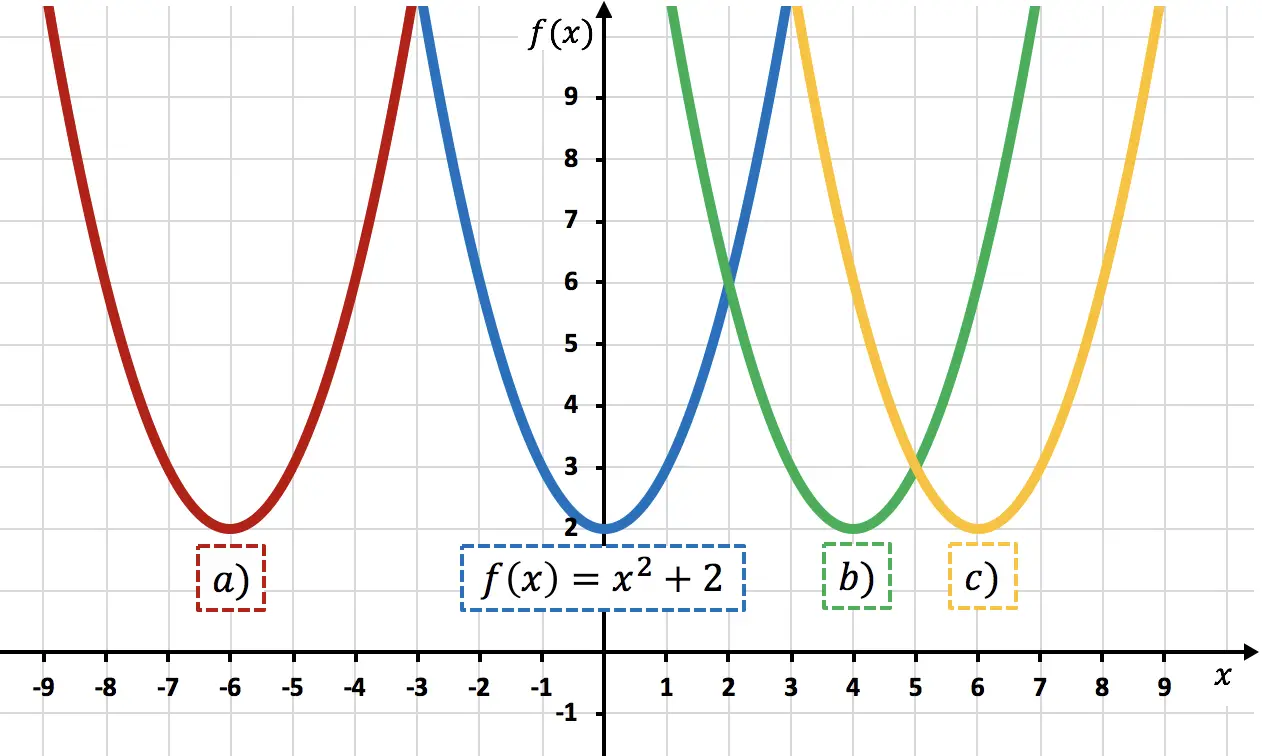
Functie

$f(x)=(x-6)^2+2$

is de functie

$f(x)=x^2+2$

6 eenheden naar rechts verplaatst. Dit kunnen we verifiëren door te berekenen

$f(x-6):$

$f(x)=x^2+2$

$f(x-6)=(x-6)^2+2$

Daarom is de vertegenwoordiging van

$f(x)=(x-6)^2+2$

komt overeen met parabool c) , omdat deze 6 eenheden naar rechts is verschoven vergeleken met

$f(x)=x^2+2$

Dit kun je zien door naar de hoekpunten van de parabolen te kijken: de afstand tussen de hoekpunten van de parabool

$f(x)=x^2+2$

en het hoekpunt van parabool c) is 6 eenheden, dus de laatste is 6 eenheden naar rechts verschoven ten opzichte van de eerste.

Functietransformaties: vertalingen, symmetrie, expansie en compressie

Wat zijn functietransformaties?

Vertalingen of bewegingen van functies

Translatie of verticale beweging van een functie

Vertaling of horizontale beweging van functies

Voorbeeld van het vertalen of verplaatsen van een functie

Reflectie of symmetrie van een functie ten opzichte van de coördinaatassen

Voorbeeld van het spiegelen van een functie

Functie-uitbreidingen en -contracties

Verticale uitzetting en inkrimping van een functie

Voorbeeld van hoe u een functie kunt uit- of samenvouwen

Opgeloste oefeningen over functietransformaties

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Oefening 5

Oefening 6

Oefening 7

Laat een reactie achter Reactie annuleren