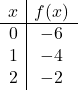Absolute waardefuncties -

Op deze pagina wordt uitgelegd wat een absolute-waardefunctie is. U leert ook hoe u een stuksgewijze absolute-waardefunctie kunt definiëren en hoe u dit soort functies in een grafiek kunt weergeven. Daarnaast zie je het met voorbeelden van absolute waardefuncties en kun je oefenen met oefeningen en stap voor stap opgeloste problemen.

Wat zijn absoluut gewaardeerde functies?

De definitie van een absolute-waardefunctie is als volgt:

De absolute waarde van een functie transformeert al zijn afbeeldingen in positieve afbeeldingen. Daarom kan het pad van een absolute functie nooit negatieve waarden hebben.

De volgende functie is een voorbeeld van een absolute-waardefunctie:

$f(x)=\lvert 5x \rvert$

Als we bij het evalueren van de functie op een bepaald punt een positief resultaat verkrijgen, blijft het positief:

$f(1)=\lvert 5\cdot 1 \rvert =\lvert 5 \rvert = 5$

Aan de andere kant, als het resultaat negatief is, wordt het positief:

$f(-1)=\lvert 5\cdot (-1) \rvert =\lvert -5 \rvert = 5$

Functies van absolute waarden worden meestal op de middelbare school gegeven, omdat ze door hun kenmerken een beetje moeilijk te begrijpen zijn.

Hoe u een functie met een absolute waarde stuksgewijs definieert

Een functie met absolute waarde kan worden uitgedrukt als een stuksgewijze functie. Om dit te doen, moet u het teken van de functie op de intervallen veranderen, wat negatief is.

Laten we een voorbeeld bekijken van hoe u van een absolute-waardefunctie naar een stuksgewijze functie kunt gaan:

Druk de volgende functie uit met een absolute waarde als een stuksgewijze functie:

$f(x) = \lvert 4 - x^2 \rvert$

Het eerste wat we moeten doen is bepalen wanneer de functie negatief is. Om dit te doen, stellen we de algebraïsche uitdrukking in op een absolute waarde gelijk aan 0 en lossen we de vergelijking op:

$4-x^2=0$

$4 = x^2$

$\sqrt{4}=\sqrt{x^2}$

$\pm 2 = x$

$x=+2 \qquad x=-2$

We vertegenwoordigen nu de verkregen waarden op de regel:

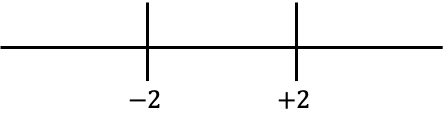
En we kijken welk teken de functie heeft zonder de absolute waarde in elk interval van de lijn:

$x<-2$

We nemen bijvoorbeeld elk punt kleiner dan -2

$x=-3:$

$4-(-3)^2$

$-5$

Negatief

$-2 < x < 2$

We nemen bijvoorbeeld elk punt tussen -2 en +2

$x=0:$

$4-0^2$

$+4$

Positief

$x>2″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”42″ style=”vertical-align: -2px;”> We nemen bijvoorbeeld elk punt groter dan 2 <p class=$ $x=3:$

$4-3^2$

$-5$

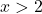
Negatief

Zoals we hebben gezien, zou de functie zonder de absolute waarde negatief zijn op de intervallen

$x<-2$

$x>2.” title=”Rendered by QuickLaTeX.com” height=”14″ width=”47″ style=”vertical-align: -2px;”> Daarom moeten we de functie in streepjes uitdrukken door het teken ervan in deze intervallen te veranderen: 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”372″ style=”vertical-align: 0px;”> 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”358″ style=”vertical-align: 0px;”> Houd er rekening mee dat u in sommige intervallen gelijkheid moet opnemen. Hier plaatsen we het bijvoorbeeld in het tweede interval <p class=$ $-2 \le x \le 2$

. Maar je kunt het in elk gewenst interval plaatsen, zolang er maar een gelijkspel is op alle kritieke punten. Met andere woorden, het zou hetzelfde zijn als we de functie als volgt hadden gedefinieerd:

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.$

Hoe een functie met een absolute waarde weer te geven

Om een functie met een absolute waarde in een grafiek weer te geven, moeten we de onderstaande stappen volgen:

Geef de functie weer alsof deze geen absolute waarde heeft.
Teken de symmetrische functie in de intervallen waarin de functie negatief is, dat wil zeggen dat deze onder de X-as ligt.
Verwijder het deel van de functie dat zich onder de X-as bevindt.

Laten we een voorbeeld bekijken van hoe u een functie met een absolute waarde kunt tekenen

Grafiek de volgende functie in absolute waarde:

$f(x) = \lvert -x+2 \rvert$

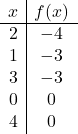
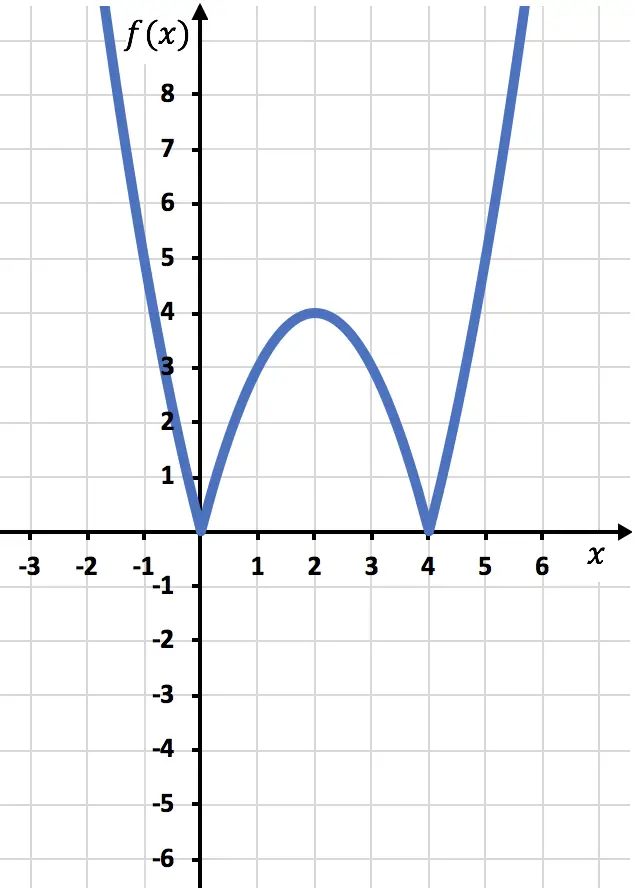
Om een functie met een absolute waarde weer te geven, moeten we eerst de functie weergeven zonder de absolute waarde. We maken daarom de tabel met functiewaarden zonder de absolute waarde:

$f(x)=-x+2$

$x= 0 \ \longrightarrow \ f(0) = -0+2=2$

$x= 1 \ \longrightarrow \ f(1) = -1+2=1$

$x= 2 \ \longrightarrow \ f(2) = -2+2=0$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 1 \\ 2 & 0 \end{array}$

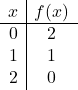
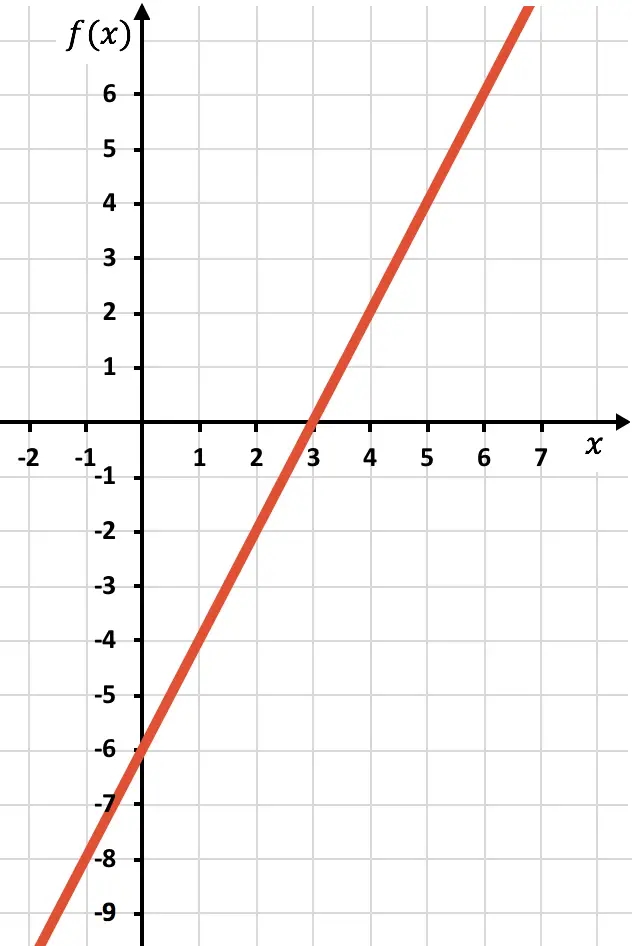
We tekenen de punten en tekenen de lijn alsof het een normale functie is:

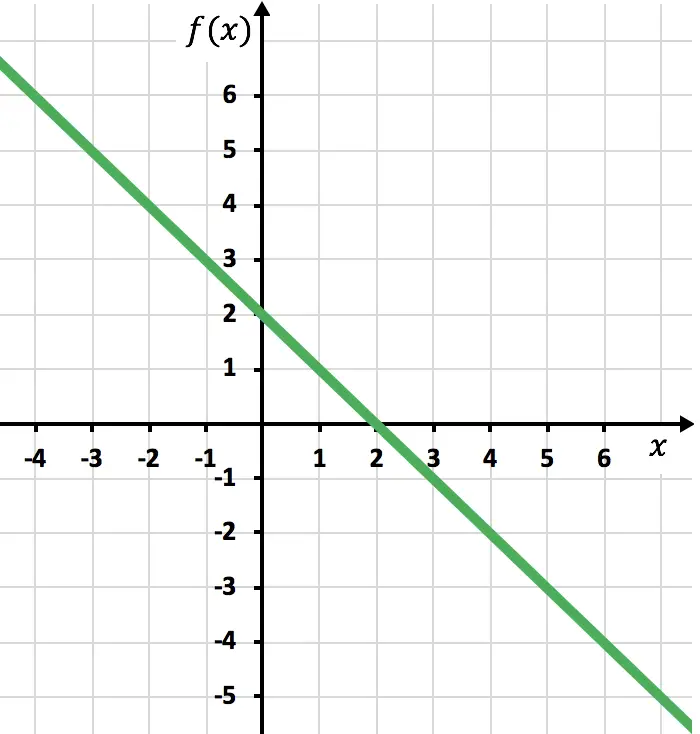
We moeten nu de symmetrische functie tekenen waar de functie negatief is, dat wil zeggen waar deze onder de x-as ligt. Daarom keren we de functie om, beginnend bij x=2:

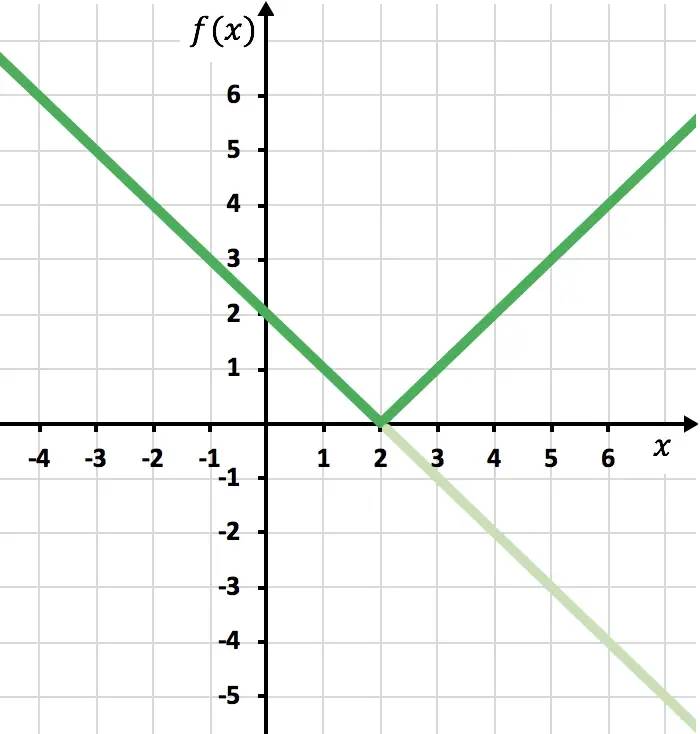
hoe je een functie met een absolute waarde representeert

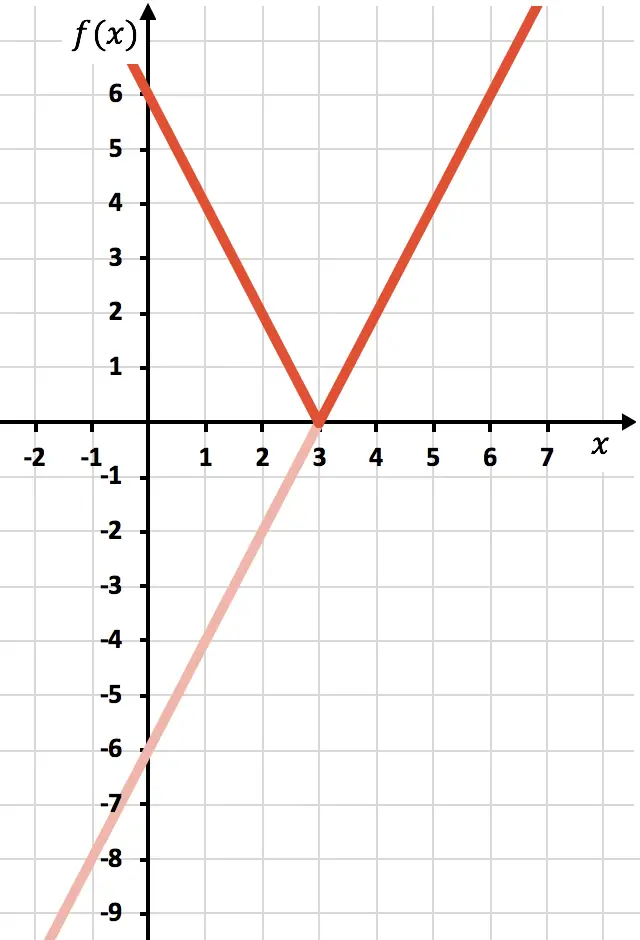
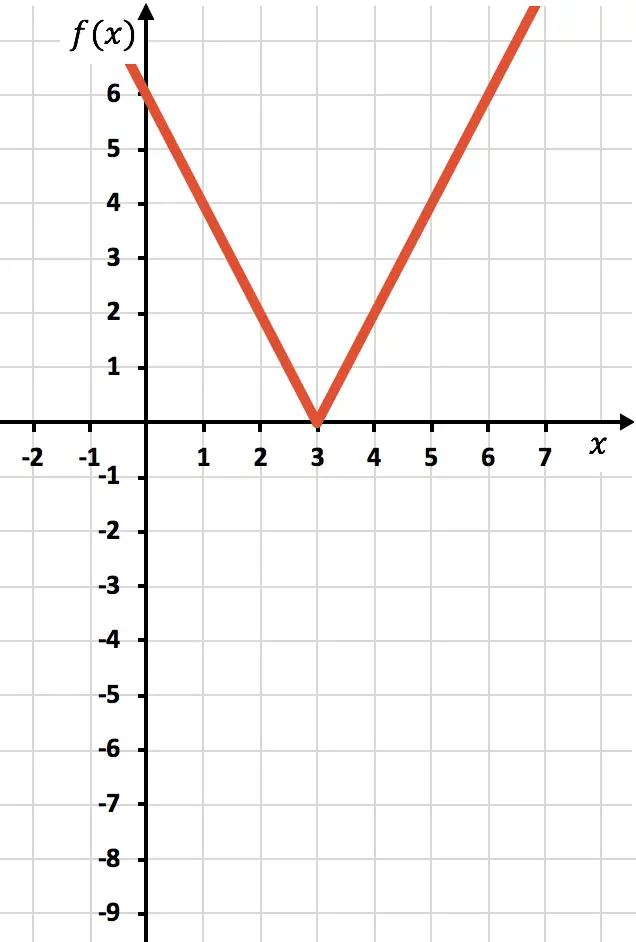
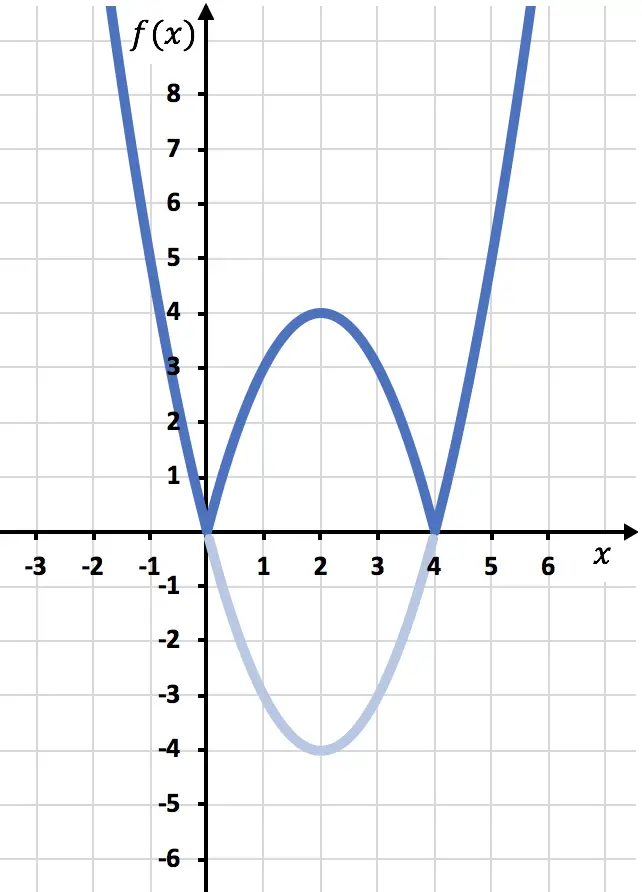
En tenslotte elimineren we het spoor van de functie dat zich onder de X-as bevindt:

hoe u een functie met een absolute waarde kunt tekenen

En op deze manier hebben we de functie al weergegeven met een absolute waarde. Zoals je hebt gezien, is het enige dat verandert, dat we het deel van de functie dat zich onder de OX-as bevindt, moeten omkeren. Daarom zal de grafiek van elke functie met een absolute waarde altijd aan de kant van de positieve semi-Y-as liggen.

Aan de andere kant, om de concepten te bekijken, kunnen we uit de grafiek afleiden dat het domein van de vorige absolute-waardefunctie volledig uit reële getallen bestaat. Aan de andere kant bestaat het bereik of bereik van genoemde functie met een absolute waarde alleen uit positieve getallen en nullen.

Opgeloste oefeningen over absolute-waardefuncties

Oefening 1

Druk de volgende functie uit met een absolute waarde als een stuksgewijze functie:

$f(x)= \lvert -x+3 \rvert$

Zie de oplossing

Allereerst moeten we kijken wanneer de functie negatief is. Om dit te doen, stellen we de absolute waarde gelijk aan nul en lossen we de vergelijking op:

$-x+3=0$

$x=3$

We vertegenwoordigen de waarde gevonden op de regel:

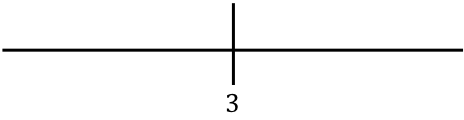
Nu evalueren we een punt in elk interval van de functie zonder de absolute waarde om erachter te komen welk teken de functie feitelijk heeft in elk deel van de lijn:

$x<3$

We nemen bijvoorbeeld elk punt kleiner dan 3

$x=0:$

$-0+3$

$+3$

Positief

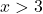$x>3″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”> <p class=$ We nemen bijvoorbeeld elk punt groter dan 3

$x=4:$

$-4+3$

$-1$

Negatief

De functie zonder de absolute waarde zou negatief zijn in het interval x>3. We moeten de functie daarom in streepjes uitdrukken door het teken in dit interval te veranderen:

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.$

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.$

Oefening 2

Zoek de stuksgewijze uitdrukking van de volgende functie met een absolute waarde:

$f(x)= \lvert 3x^2-75 \rvert$

Zie de oplossing

Het eerste wat we moeten doen is bepalen wanneer de functie negatief is. Om dit te doen, moeten we het argument voor de absolute waarde gelijk stellen aan nul en de vergelijking oplossen:

$3x^2-75 =0$

$3x^2=75$

$x^2=\cfrac{75}{3}$

$x^2=25$

$x= \pm 5$

We vertegenwoordigen nu de wortels van de functie die we aan de rechterkant hebben verkregen:

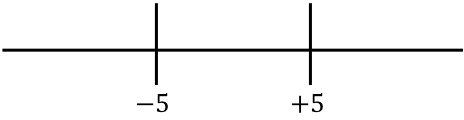
En we kijken welk teken de functie heeft zonder de absolute waarde in elk interval van de lijn:

$x<-5$

We nemen bijvoorbeeld elk punt kleiner dan -5

$x=-6:$

$3(-6)^2-75$

$108-75$

$+33$

Positief

$-5 < x < 5$

We nemen bijvoorbeeld elk punt tussen -5 en +5

$x=0:$

$3(0)^2-75$

$0-75$

$-75$

Negatief

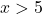$x>5″ title=”Rendered by QuickLaTeX.com” height=”15″ width=”42″ style=”vertical-align: -2px;”> <p class=$ We nemen bijvoorbeeld elk punt groter dan 5

$x=6:$

$3(6)^2-75$

$108-75$

$+33$

Positief

Daarom zou de functie zonder de absolute waarde alleen negatief zijn in het interval -5<x<5. Daarom moeten we de functie in delen uitdrukken door alleen het teken van dit interval te veranderen:

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”408″ style=”vertical-align: 0px;”> 5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”394″ style=”vertical-align: 0px;”> <div class=$

Oefening 3

Om een functie met een absolute waarde weer te geven, moet u eerst de functie weergeven zonder de absolute waarde:

Het is een affiene functie, dus je moet een tabel met waarden construeren om deze grafisch weer te geven:

We moeten nu de symmetrische functie tekenen waar de functie negatief is, dat wil zeggen waar deze onder de X-as ligt. Daarom keren we de functie om van x=3 naar achteren:

En ten slotte elimineren we het deel van de functie dat zich onder de X-as bevindt:

Oefening 4

Om een functie met een absolute waarde weer te geven, moeten we eerst de functie tekenen zonder de absolute waarde.

Dit is een kwadratische functie. Om dit weer te geven, moeten we daarom de X-coördinaat van de top van de parabool berekenen met de formule:

We moeten nu de functie vertalen door symmetrie waar deze negatief is, dat wil zeggen waar deze zich onder de OX-as bevindt. Daarom keren we de functie om van x=0 naar x=4:

En ten slotte verwijderen we het deel van de functie dat zich onder de X-as bevindt: