Lineaire functie en affiene functie -

In dit artikel vind je de uitleg van de affiene functie en de lineaire functie, evenals de verschillen die er bestaan tussen deze twee soorten functies. Daarnaast ziet u voorbeelden van hoe u een affiene functie en een lineaire functie kunt tekenen en hoe u hun uitdrukkingen vanuit twee punten kunt berekenen. Ten slotte kun je trainen met verschillende oefeningen die stap voor stap worden opgelost.

Wat is een affiene functie en een lineaire functie?

De definities van de affiene functie en de lineaire functie zijn als volgt:

Een affiene functie is een polynomiale functie van de eerste graad, dat wil zeggen een functie die, weergegeven in de grafiek, een rechte lijn is. De bijbehorende functies zijn als volgt:

$f(x)=mx+n$

Goud

$m$

is de helling van de lijn en

$n$

Dit is het y-snijpunt, dat wil zeggen waar de functie de verticale as snijdt.

In de wiskunde worden affiene functies in de context van lineaire algebra ook wel lineaire transformaties genoemd.

Een lineaire functie is een affiene functie die geen onafhankelijke term heeft. Daarom is de formule voor lineaire functies:

$f(x)=mx$

Goud

$m$

is de helling van de lijn.

Het domein en bereik (of bereik) van de lineaire functie en de affiene functie zijn allemaal reële getallen:

$\text{Dom } f=\mathbff{R}$

$\text{Im } f= \mathbb{R}$

Wat is het verschil tussen een lineaire functie en een affiene functie?

Nu je de concepten van lineaire functie en affiene functie hebt gezien, zul je gemerkt hebben dat ze erg op elkaar lijken. Het volgende verschil tussen beide is echter erg belangrijk:

Het enige verschil tussen de lineaire functie en de affiene functie is dat de lineaire functie geen onafhankelijke term heeft, terwijl de affiene functie altijd de coëfficiënt van het snijpunt (n) heeft die verschilt van nul (0).

Lineaire functie

$f(x)=mx$

lineaire functie

$f(x)=mx+n$

Dit impliceert dat een lineaire functie altijd door de coördinaatoorsprong gaat , het punt (0,0). Aan de andere kant zal een affiene functie nooit door dit punt gaan omdat deze een ander snijpunt dan 0 heeft.

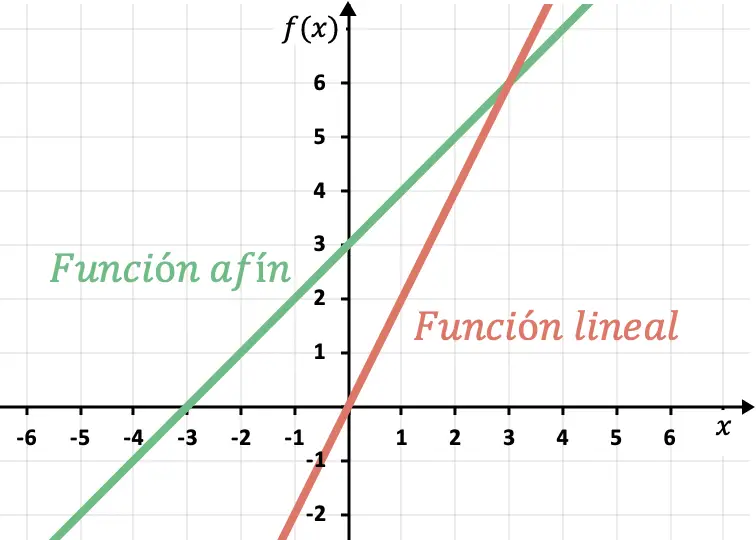
Wat is het verschil tussen een lineaire functie en een affiene functie?

Helling en y-snijpunt van een lineaire of affiene functie

In deze sectie analyseren we een voorbeeld van een affiene of lineaire functie om de betekenis van de termen te begrijpen

$m$

$n$

, of met andere woorden, de helling en het y-snijpunt.

Bepaal de uitdrukking voor de functie die in de grafiek wordt weergegeven en classificeer deze als een lineaire of affiene functie.

Dit soort functies volgt de volgende uitdrukking:

$f(x)=mx+n$

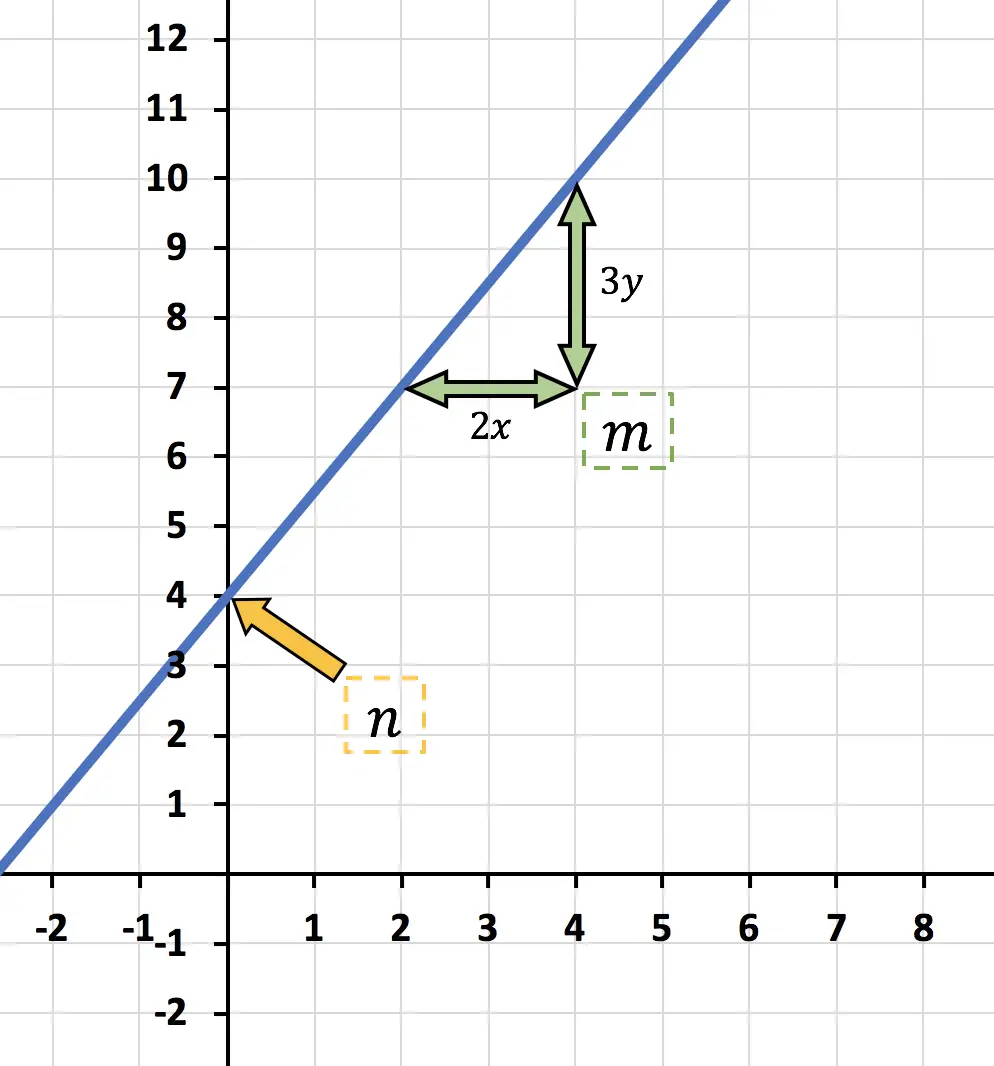
wat betekent helling en y-snijpunt lineaire of affiene functie m en n

$n$

Dit is het y-snijpunt, dat wil zeggen waar de functie de verticale Y-as snijdt. Dus in dit geval:

$n=4$

Aan een andere kant,

$m$

is de helling van de lijn. Y kan worden berekend door het verschil in y tussen twee punten te delen door het verschil in x tussen dezelfde twee punten:

$m=\cfrac{\Delta y }{\Delta x} = \cfrac{3}{2}$

$m$

zegt “hoeveel y toeneemt voor elke x” , dus in dit geval neemt de functie “3y toe voor elke 2x” .

Concluderend is de uitdrukking voor de affiene functie weergegeven in de grafiek:

$\displaystyle \bm{f(x)=}\frac{\bm{3}}{\bm{2}}\bm{x+4}$

Omdat het y-snijpunt niet nul is, is het bovendien een affiene functie .

Hieronder laten we u meer voorbeelden zien van lineaire en affiene functies om uw begrip te vervolledigen:

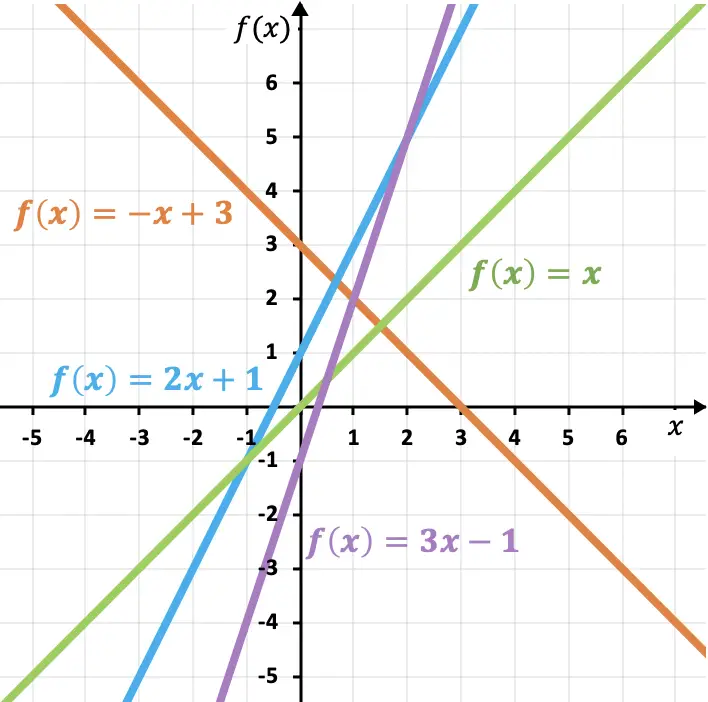
voorbeelden van lineaire en affiene functies

Zoals u in deze voorbeelden kunt zien, geldt: hoe groter de helling, hoe steiler de lijn en dus hoe groter de functie. Op dezelfde manier bepaalt de hellingscoëfficiënt de groei of afname van een functie:

Als de helling positief is, neemt de functie toe , dat wil zeggen dat deze toeneemt naarmate x toeneemt.
Als de helling negatief is, neemt de functie af , dat wil zeggen dat deze afneemt naarmate x toeneemt.

Bovendien kun je ook zien of twee lijnen evenwijdig of loodrecht zijn op hun hellingen:

Wanneer twee lijnen dezelfde helling hebben, zijn ze evenwijdig , dat wil zeggen dat ze elkaar op geen enkel punt snijden of volledig identiek zijn.

$m_1 = m_2$

Aan de andere kant staan twee lijnen loodrecht , dat wil zeggen dat ze elkaar snijden onder een verticale hoek (90º), als hun hellingen overeenkomen met de volgende relatie:

$m_1 = -\cfrac{1}{m_2}$

Voorbeeld van weergave van een affiene of lineaire functie

Laten we eens kijken hoe we een eerstegraadsfunctie kunnen tekenen aan de hand van een voorbeeld.

Grafiek de volgende affiene functie:

$f(x)=2x-1$

Het eerste wat we moeten doen is een array van waarden creëren. Om dit te doen, verlenen we de waarden die we willen

$x$

waarden te verkrijgen van

$f(x)$

$f(x)=2x-1$

$x= 0 \ \longrightarrow \ f(0) = 2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1) = 2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2) = 2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3) = 2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4) = 2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

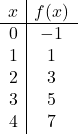
Hoewel een waardentabel met twee punten voldoende is, kunnen we meer punten doen om er zeker van te zijn dat deze correct is.

Nadat we de waardentabel hebben gemaakt, zetten we de punten in de grafiek in kaart:

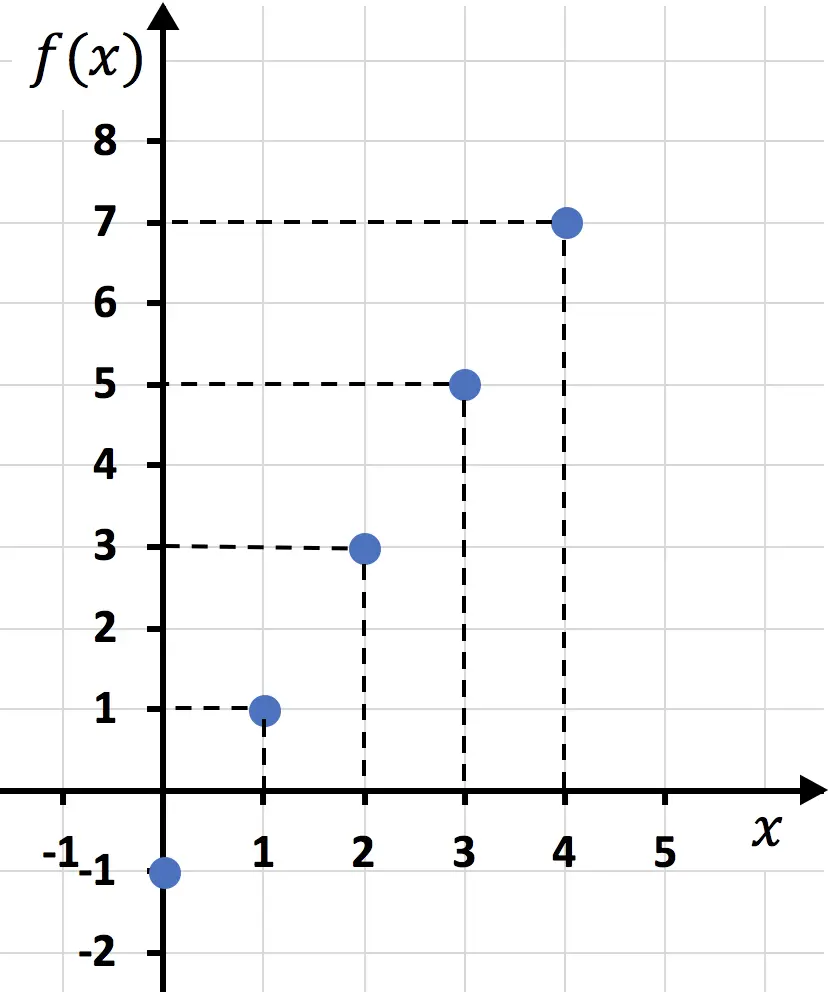
hoe je een lijn of een lineaire functie of en affiene voorstelt

En ten slotte voegen we de punten samen en trekken een lijn:

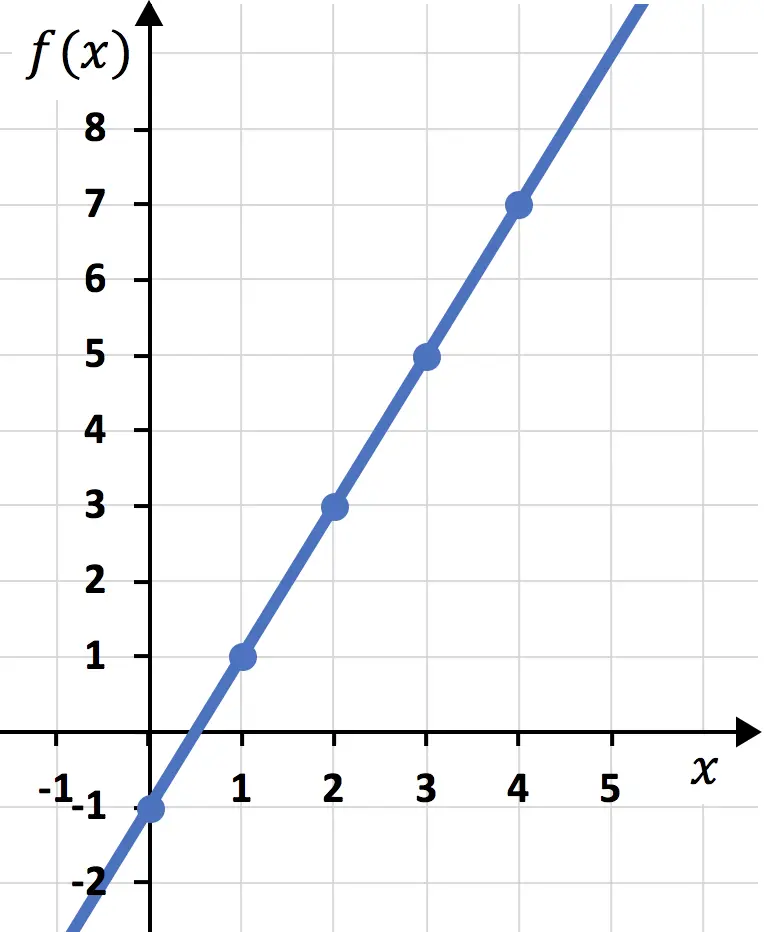
grafische weergave van een lineaire of affiene functie

En op deze manier hebben we de functie al in een grafiek weergegeven. Zoals u kunt zien, is het niet ingewikkeld. U hoeft alleen maar eerst een tabel met waarden te maken en vervolgens de punten in een grafiek uit te zetten.

Hoe een lineaire of affiene functie vanuit twee punten te berekenen

Laten we nu eens kijken hoe we een lineaire of affiene functie uit twee punten kunnen vinden met behulp van een voorbeeld:

Bereken de lineaire functie die voldoet
$f(3)=5$

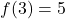
en ga door het punt

$(1,-1).$

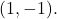
Allereerst,

$f(3)=5$

Dit betekent dat de functie door het punt gaat

$(3,5)$

Omdat we twee punten hebben waar de functie doorheen gaat, kunnen we de helling berekenen

$m$

functie:

Als we twee punten overwegen,

$P_1=(x_1,y_1)$

$P_2=(x_2,y_2)$

, helling

$m$

van de functie wordt berekend:

$m=\cfrac{y_2-y_1}{x_2-x_1}$

In ons geval gaat de functie door de punten

$(3,5)$

$(1,-1)$

. De helling dus

$m$

van de functie is:

$m=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-1-5}{1-3} = \cfrac{-6}{-2} = 3$

De functie zal daarom de vorm hebben:

$f(x) = mx+n \ \xrightarrow{m \ = \ 3} \ f(x)=3x+n$

Zodra we het weten

$m$

wij kunnen het mysterie oplossen

$n$

. Om dit te doen, vervangen we de coördinaten van een punt dat bij de functie hoort in de vergelijking. Bijvoorbeeld punt (3.5):

$f(x) = 3x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ 5} \ 5=3\cdot 3+n$

We lossen de resulterende vergelijking op:

$5=3\cdot 3+n$

$5= 9 + n$

$5-9=n$

$-4=n$

De lineaire functie is daarom:

$\bm{f(x)=3x-4}$

Opgeloste oefeningen over lineaire en affiene functies

Oefening 1

Bepaal de helling en oorsprong van de volgende affiene functie:

$f(x)=-5x-2$

Zie de oplossing

Een lineaire functie heeft de vorm

$f(x)=mx+n .$

De helling van de functie is dus het getal dat bij x hoort, wat in dit geval -5 is:

$\bm{m=-5}$

En het y-snijpunt is de onafhankelijke term, in dit geval -2:

$\bm{n=-2}$

Oefening 2

Grafiek de volgende affiene functie:

$f(x)=x+1$

Zie de oplossing

We geven er eerst waarden aan

$x$

om de waardentabel te maken:

$x= 0 \ \longrightarrow \ f(0)=0+1 = 1$

$x= 1 \ \longrightarrow \ f(1)=1+1= 2$

$x= 2 \ \longrightarrow \ f(2)=2+1 = 3$

$x= 3 \ \longrightarrow \ f(3)=3+1 = 4$

$x= 4 \ \longrightarrow \ f(4)=4+1 = 5$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \\ 3 & 4 \\ 4 & 5 \end{array}$

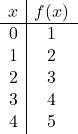
En dan vertegenwoordigen we de punten uit de waardentabel in de grafiek en trekken we de lijn:

voorbeeld van een lineaire of affiene functie

Oefening 3

Teken de volgende affiene functie in de grafiek:

$f(x)=-2x+6$

Zie de oplossing

We geven er eerst waarden aan

$x$

om de waardentabel te maken:

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0+6=6$

$x= 1 \ \longrightarrow \ f(1)=-2\cdot1+6=4$

$x= 2 \ \longrightarrow \ f(2)=-2\cdot2+6=2$

$x= 3 \ \longrightarrow \ f(3)=-2\cdot3+6=0$

$x= 4 \ \longrightarrow \ f(4)=-2\cdot4+6=-2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 6 \\ 1 & 4 \\ 2 & 2 \\ 3 & 0 \\ 4 & -2 \end{array}$

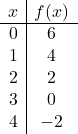
En ten slotte vertegenwoordigen we de punten uit de waardentabel in de grafiek en trekken we de lijn:

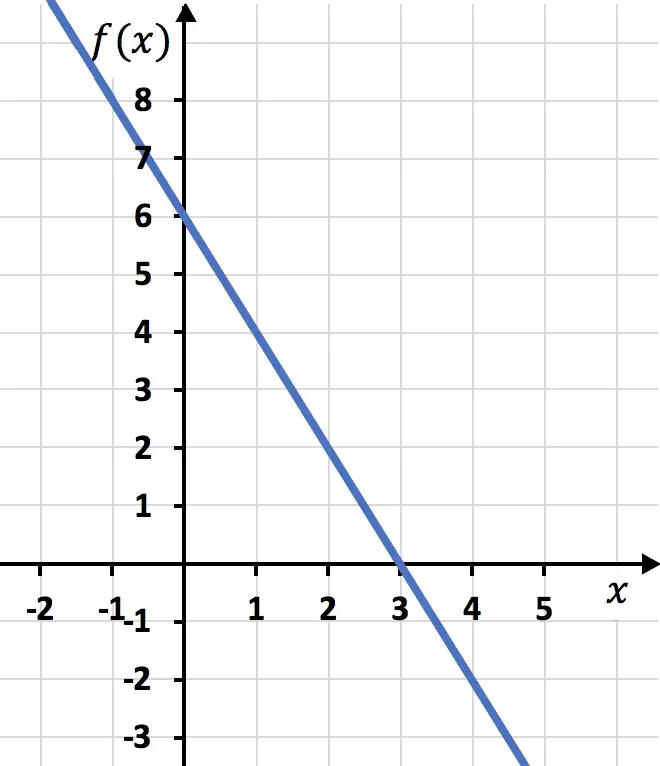
oefening stap voor stap opgelost van lineaire en affiene functie

Oefening 4

Zoek de uitdrukking voor de affiene functie die door de punten (2,3) en (0,1) gaat.

Zie de oplossing

De functie gaat door de punten (2,3) en (0,1), dus de helling van de functie is:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{1-3}{0-2} = \cfrac{-2}{-2} = 1$

En de functie heeft de vorm:

$f(x)=mx+n \ \xrightarrow{m \ = \ 1} \ f(x)=1x+n$

Zodra we m kennen, kunnen we n berekenen. Om dit te doen, moeten we de coördinaten van een punt dat bij de functie hoort, in de vergelijking vervangen. Bijvoorbeeld punt (2,3):

$f(x)=x+n \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 3}$

$3=2+n$

We moeten nu de resulterende vergelijking oplossen:

$3-2=n$

$1 = n$

De functie komt daarom overeen met de volgende uitdrukking:

$\bm{f(x)=x+1}$

Oefening 5

Grafiek de volgende affiene functie:

$f(x)=2x-1$

Zie de oplossing

We geven er eerst waarden aan

$x$

om de waardentabel te maken:

$x= 0 \ \longrightarrow \ f(0)=2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1)=2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2)=2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3)=2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4)=2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

En dan vertegenwoordigen we de punten uit de waardentabel in de grafiek en trekken we de lijn:

Opgeloste oefeningen om een lineaire of affiene functie te tekenen

Oefening 6

Bereken de lineaire functie die aan de volgende twee voorwaarden voldoet:

$\begin{array}{c}f(3) =-2 \\[3ex] f(-1)=6 \end{array}$

Zie de oplossing

Moge het werkelijkheid worden

$f(3)=-2$

Dit betekent dat de functie door het punt (3,-2) gaat. En op dezelfde manier

$f(-1)=6$

Dit betekent dat de functie door het punt (-1,6) gaat.

Dus de functie gaat door de punten (3,-2) en (-1,6), dus de helling is:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{6-(-2)}{-1-3} = \cfrac{8}{-4} = -2$

De functie zal daarom de vorm hebben:

$f(x)=mx+n \ \xrightarrow{m \ = \ -2} \ f(x)=-2x+n$

En zodra we m kennen, kunnen we n berekenen. Om dit te doen, vervangen we de coördinaten van een punt dat bij de functie hoort in de vergelijking. Bijvoorbeeld het punt (3,-2):

$f(x)=-2x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ -2} \ -2=-2(3)+n$

En we lossen de resulterende vergelijking op:

$-2=-6+n$

$-2+6=n$

$4 = n$

De functie is dus:

$\bm{f(x)=-2x+4}$

Oefening 7

Zoek de affiene functie die het uitvoert

$f(1) =6$

en gaat door het punt (3.5).

Zie de oplossing

Moge het werkelijkheid worden

$f(1)=6$

Dit betekent dat de functie door het punt (1,6) gaat.

De functie gaat daarom door de punten (1.6) en (3.5) en daarom is de helling:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{5-6}{3-1} = \cfrac{-1}{2} = -\cfrac{1}{2}$

De functie zal daarom de vorm hebben:

$\displaystyle f(x)=mx+n \ \xrightarrow{m \ = \ -\frac{1}{2}} \ f(x)=-\frac{1}{2}x+n$

Zodra we de term m kennen, kunnen we de coëfficiënt n berekenen. Om dit te doen, vervangen we de coördinaten van een punt dat bij de functie hoort in de vergelijking. Bijvoorbeeld het punt (1,6):

$\displaystyle f(x)=-\frac{1}{2}x+n \ \xrightarrow{x \ = \ 1 \ ; \ f(x) \ = \ 6} \ 6=-\frac{1}{2}\cdot 1+n$

We lossen de resulterende vergelijking op:

$6=-\cfrac{1}{2}+n$

$6+\cfrac{1}{2}=n$

Onthoud dat als u breuken wilt optellen, u ze eerst moet terugbrengen tot een gemeenschappelijke noemer en vervolgens de tellers moet optellen:

$\cfrac{2 \cdot 6}{2} +\cfrac{1 \cdot 1}{2}=n$

$\cfrac{12}{2} +\cfrac{1}{2}=n$

$\cfrac{13}{2}=n$

De functie is dus:

$\displaystyle \bm{f(x)=-}\mathbf{\frac{1}{2}}\bm{x +}\mathbf{\frac{13}{2}}$

Oefening 8

Los het volgende probleem op met betrekking tot lineaire en affiene functies:

Een winkel verkoopt 40 stuks van een product als de prijs € 15/stuk is, en 65 stuks als de prijs € 10/stuk is.

Bereken de vraagfunctie voor het product, ervan uitgaande dat het een affiene functie is.
Hoeveel eenheden worden er verkocht als de prijs is vastgesteld op € 12/eenheid?

Zie de oplossing

Omdat het een affiene functie is, zal de functie van het type zijn

$f(x)=mx+n .$

Goud

$x$

is de eenheidsprijs van het product en

$f(x)$

zullen de verkochte eenheden zijn.

Het persbericht vertelt ons dat wanneer de prijs € 15/stuk bedraagt, er 40 stuks verkocht worden. Daarom, als

$x$

is de prijs en

$f(x)$

verkochte eenheden, moet de volgende gelijkheid gerespecteerd worden:

$f(15)=40$

En als de prijs € 10/stuk bedraagt, worden er 65 stuks verkocht. Dus, met dezelfde redenering:

$f(10)=65$

Moge het werkelijkheid worden

$f(15)=40$

Dit betekent dat de functie door het punt (15.40) gaat. EN

$f(10)=65$

Dit betekent dat de functie door het punt (10.65) gaat.

De helling van de functie is daarom:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{65-40}{10-15} = \cfrac{25}{-5} = -5$

De functie zal daarom de vorm hebben:

$f(x)=mx+n \ \xrightarrow{m \ = \ -5} \ f(x)=-5x+n$

Zodra we m kennen, kunnen we n berekenen. Om dit te doen, vervangen we de coördinaten van een punt dat bij de functie hoort in de vergelijking. Bijvoorbeeld het punt (15:40 uur):

$f(x)=-5x+n \ \xrightarrow{x \ = \ 15 \ ; \ f(x) \ = \ 40} \ 40=-5\cdot 15+n$