In dit artikel leggen we uit hoe je de hyperbolische boogcotangens van een functie kunt afleiden. Bovendien kunt u opgeloste voorbeelden zien van de afgeleide van de hyperbolische boogcotangens.
Formule voor de afgeleide van de hyperbolische boogcotangens
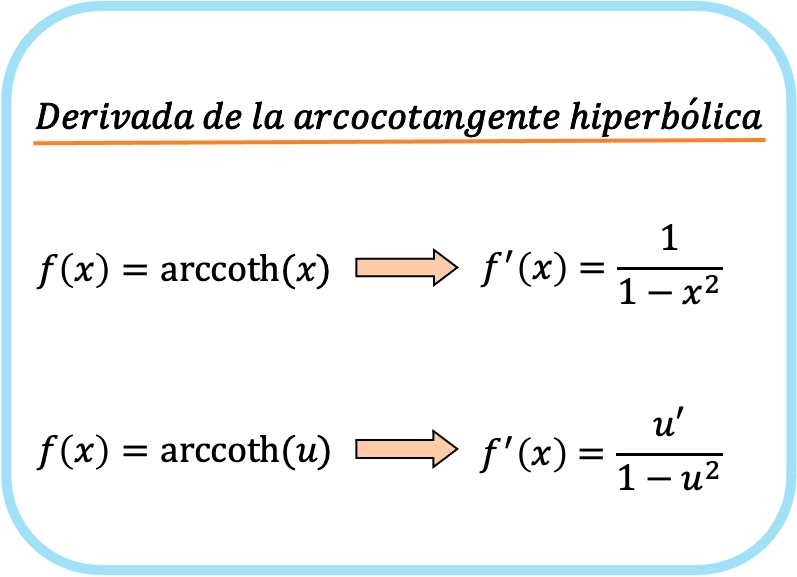
De afgeleide van de hyperbolische boogcotangens van x is één gedeeld door één minus x kwadraat.
![]()
Daarom is de afgeleide van de hyperbolische boogcotangens van een functie gelijk aan het quotiënt van de afgeleide van die functie gedeeld door één minus die functie in het kwadraat.
![]()
Merk op dat de tweede formule hetzelfde is als de eerste, maar de kettingregel toepast, zodat ze feitelijk als dezelfde formule kunnen worden beschouwd.
In sommige wiskundeboeken zie je misschien dat de afgeleide van dit type inverse trigonometrische functie:
![]()
Als je echter goed kijkt, zijn het dezelfde formules, het enige verschil is dat de teller en de noemer van de breuk met -1 zijn vermenigvuldigd.
Voorbeelden van afgeleide van de hyperbolische boogcotangens
voorbeeld 1
![]()
In het hyperbolische boogcotangens-argument hebben we een functie die verschilt van x, dus we moeten de kettingregelformule gebruiken om deze af te leiden:
![]()
De afgeleide van 5x is 5, dus plaats een 5 in de teller van de breuk en een min 5x kwadraat in de noemer:
![]()
Voorbeeld 2
![]()
Om de afgeleide van deze functie op te lossen, moeten we de formule voor de afgeleide van de hyperbolische boogcotangens toepassen, die als volgt is:
![]()
In dit geval hebben we een samengestelde functie, omdat er een exponentiële functie is in het argument van de trigonometrische functie. We moeten dus de kettingregel gebruiken om de afgeleide van de gehele functie te vinden:
![]()