Hyperbolische cosecante boogafgeleide

In dit artikel leggen we uit hoe je de hyperbolische boogcosecans van een functie kunt afleiden. U zult ook uitgewerkte voorbeelden vinden van de afgeleide van de hyperbolische arccosecant.

Formule voor de afgeleide van de hyperbolische cosecansboog

De afgeleide van de boog-hyperbolische cosecans van x is gelijk aan negatief 1 gedeeld door het product van x maal de wortel van één plus x kwadraat.

f(x)=\text{arccsch}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-1}{x\sqrt{1+x^2}}

Daarom is de afgeleide van de boog-hyperbolische cosecans van een functie minus de afgeleide van de genoemde functie gedeeld door het product van de functie maal de wortel van één plus de kwadratische functie.

f(x)=\text{arccsch}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1+u^2}}

Samenvattend is de formule voor het berekenen van de afgeleide van de hyperbolische boogcosecante functie:

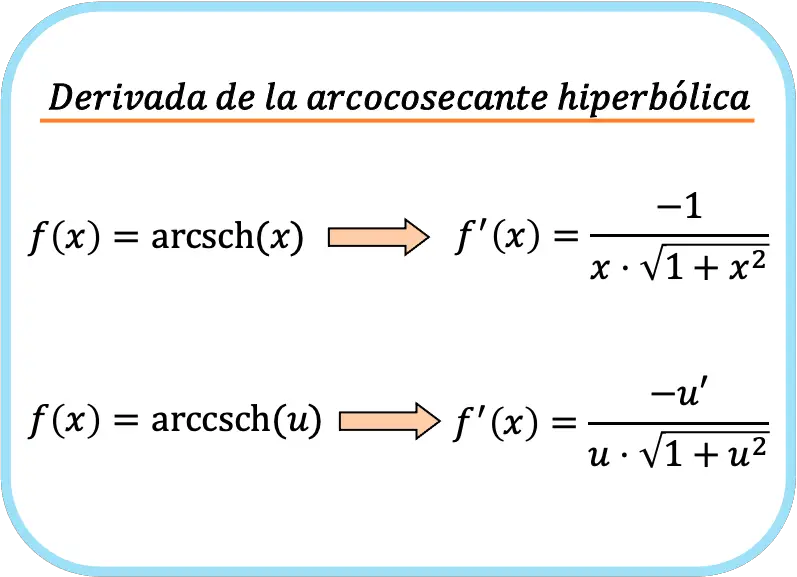
afgeleide van de hyperbolische cosecante boog

Hoewel we twee formules hebben opgesteld, betekent dit niet dat ze verschillend zijn. Als je goed kijkt, lijkt de tweede formule op de eerste, maar wordt de kettingregel toegepast.

Voorbeelden van de afgeleide van de hyperbolische cosecansboog

Gegeven de formule voor de afgeleide van de hyperbolische boog-cosecans, zullen we vervolgens twee van dergelijke functies afleiden, zodat je kunt zien hoe het werkt.

voorbeeld 1

f(x)=\text{arccsch}(3x)

In deze oefening moeten we de formule gebruiken voor de afgeleide van de boog-hyperbolische cosecans met de kettingregel, omdat er in het argument een andere functie is dan x:

f(x)=\text{arccsch}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1+u^2}}

Om de afgeleide te vinden, moeten we dus de u vervangen door 3x en de u’ door zijn afgeleide, namelijk 3:

f(x)=\text{arccsch}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-3}{3x\sqrt{1+(3x)^2}}=\cfrac{-3}{3x\sqrt{1+9x^2}}

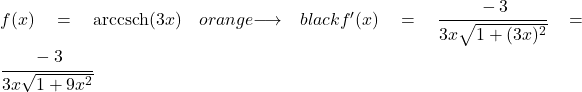
Voorbeeld 2

f(x)=\text{arccsch}(x^5-2x^3)

In dit geval hebben we een polynomiale functie in het hyperbolische boogcosecante argument, dus we moeten ook de kettingregel gebruiken om deze af te leiden:

f(x)=\text{arccsch}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{-u'}{u\sqrt{1+u^2}}

Dus plaatsen we de afgeleide van de argumentfunctie in de teller van de breuk, en in de noemer veranderen we de u met de polynoomfunctie:

\begin{aligned}f(x)=\text{arccsch}(x^5-2x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(5x^4-6x^2)}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\\[1.5ex] &=\cfrac{-5x^4+6x^2}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\end{aligned}

Gelijkwaardige producten

Laat een reactie achter

Je e-mailadres wordt niet gepubliceerd. Vereiste velden zijn gemarkeerd met *

Scroll naar boven