Hier leest u hoe u de afgeleide van de hyperbolische boogsecans van een functie kunt berekenen. Bovendien kunt u opgeloste voorbeelden zien van de afgeleide van de hyperbolische boogsecans.
Hyperbolische arcsecant-afgeleide formule
De afgeleide van de hyperbolische boogsecans van x is gelijk aan negatief 1 gedeeld door het product van x maal de wortel van één minus x kwadraat.
![]()
Daarom is de afgeleide van de hyperbolische boogsecans van een functie minus de afgeleide van die functie gedeeld door het product van de functie maal de wortel van één minus de kwadratische functie.
![]()
Kortom, de formule voor de afgeleide van de hyperbolische boogsecansfunctie is:
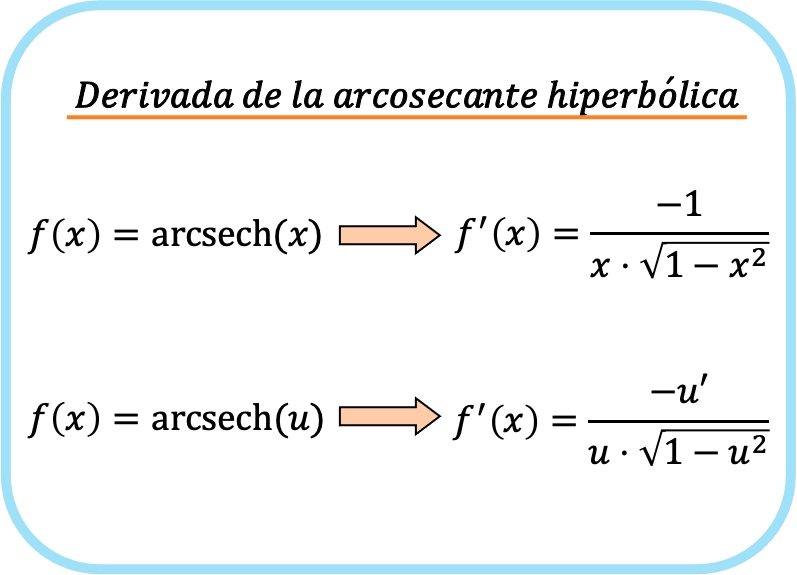
Beide uitdrukkingen komen feitelijk overeen met dezelfde formule, maar op de tweede formule wordt de kettingregel toegepast. Als je u vervangt door de identiteitsfunctie x, krijg je de eerste formule, aangezien de afgeleide van x 1 is.
Voorbeelden van afgeleide van de hyperbolische boogsecans
Nadat we hebben gezien wat de formule is voor de afgeleide van de hyperbolische boogsecans, zullen we twee stapsgewijze oefeningen van dit type inverse trigonometrische afgeleiden oplossen. U kunt dus precies zien hoe u de hyperbolische boogsecans van een functie kunt afleiden.
voorbeeld 1
In dit voorbeeld gaan we bepalen wat de afgeleide van de 2x hyperbolische boogsecans is.
![]()
In het hyperbolische boogsecans-argument hebben we een andere functie dan x, dus we moeten de kettingregelformule gebruiken om deze af te leiden:
![]()
De functie 2x is lineair, dus de afgeleide ervan is 2. Om de afgeleide te vinden, vervangen we daarom eenvoudigweg 2x voor u en 2 voor u’ in de formule:
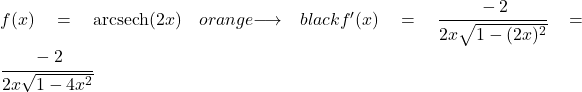
Voorbeeld 2
In deze tweede oefening zullen we de hyperbolische boogsecans van een polynoomfunctie afleiden:
![]()
De functie van deze oefening is samengesteld, omdat de hyperbolische boogsecant een andere functie heeft in zijn argumentatie. We moeten dus de hyperbolische afgeleide formule van de boogsecant gebruiken met de kettingregel om de afleiding te doen:
![]()
Daarom plaatsen we in de teller van de breuk de afgeleide van de polynoomfunctie van het argument, en in de noemer veranderen we de u door de polynoomfunctie:
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arcsech}(x^3-4x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(3x^2-4)}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\\[1.5ex] &=\cfrac{-3x^2+4}{(x^3-4x)\sqrt{1-(x^3-4x)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1f6389de5c7761fb5d35a9861156eec1_l3.png)