In dit artikel leggen we uit hoe je de hyperbolische cosecans van een functie kunt afleiden. Bovendien zult u verschillende opgeloste voorbeelden kunnen zien van de afgeleide van de hyperbolische cosecans.
Formule voor de afgeleide van de hyperbolische cosecans
De afgeleide van de hyperbolische cosecans van x is gelijk aan minus de hyperbolische cosecans van x maal de hyperbolische cotangens van x.
![]()
Daarom is de afgeleide van de hyperbolische cosecans van een functie minus het product van de hyperbolische cosecans van de functie maal de hyperbolische cotangens van de functie maal de afgeleide van de genoemde functie.
![]()
Kort gezegd is de formule voor het afleiden van de cosecans van een functie:
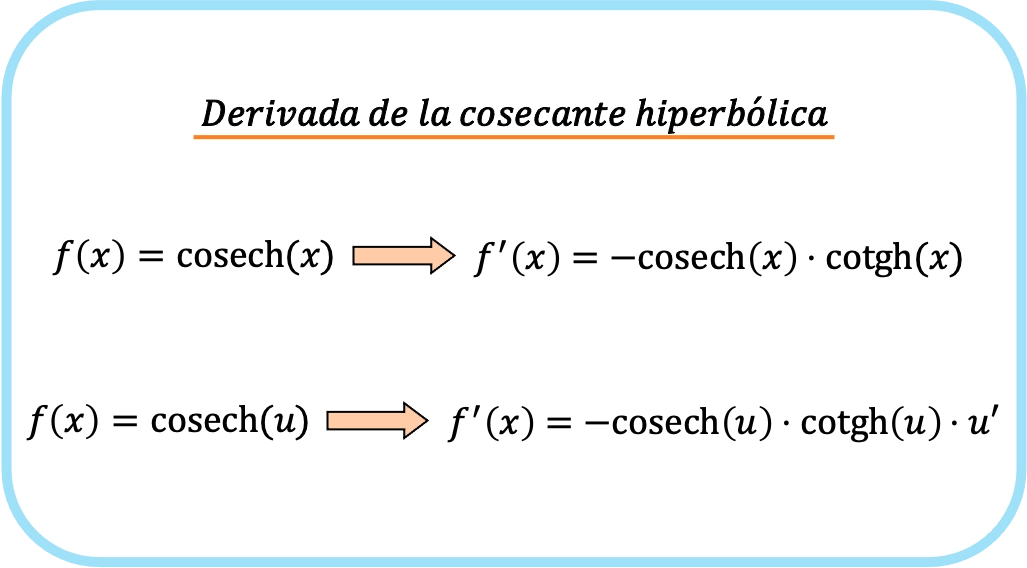
In feite komen de voorgaande twee uitdrukkingen overeen met één enkele formule, het verschil is dat in de tweede formule de kettingregel wordt toegepast.
Voorbeelden van afgeleide van de hyperbolische cosecans
Nadat we hebben gezien wat de formule is voor de afgeleide van de hyperbolische cosecans, volgen hier verschillende uitgewerkte voorbeelden van dit type trigonometrische afgeleide.
voorbeeld 1
In dit eerste voorbeeld zullen we de hyperbolische cosecans van x kwadraat afleiden:
![]()
De functie van het argument van de hyperbolische cosecans is anders dan x, dus we moeten de formule gebruiken voor de afgeleide van de hyperbolische cosecans met de kettingregel.
![]()
Dus om deze trigonometrische functie af te leiden, hoeven we alleen maar de waarden in de vorige formule te vervangen, dat wil zeggen dat we in het argument van de hyperbolische cosecans en de hyperbolische tangens x 2 plaatsen, en we vermenigvuldigen alles met de afgeleide van x kwadraat, wat 2x is:
![]()
Voorbeeld 2
In deze oefening zullen we zien hoeveel de afgeleide is van de hyperbolische cosecans van x in de derde macht:
![]()
Om de afgeleide van de hyperbolische cosecans van een functie te vinden, passen we de formule toe:
![]()
De afgeleide van x in de derde macht is 3x 2 , dus de afgeleide van de gehele functie is:
![]()