In dit artikel leggen we uit hoe je de secans hyperbolicus van een functie kunt afleiden. U vindt de formule voor de afgeleide van de secans hyperbolicus en verschillende uitgewerkte voorbeelden van dit type afgeleide.
Formule voor de afgeleide van de secans hyperbolicus
De afgeleide van de secans hyperbolicus van x is gelijk aan minus het product van de secans hyperbolicus van x maal de tangens hyperbolicus van x.
![]()
Daarom is de afgeleide van de hyperbolische secans van een functie minus het product van de hyperbolische secans van de functie maal de hyperbolische tangens van de functie maal de afgeleide van de genoemde functie.
![]()
Kort gezegd is de formule voor de afgeleide van de hyperbolische secansfunctie:
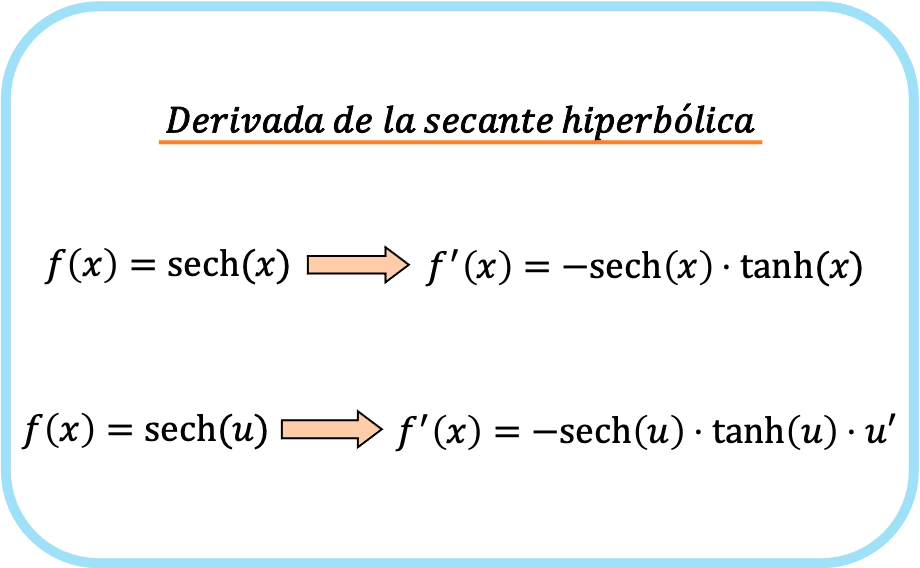
Merk op dat beide uitdrukkingen feitelijk tot één enkele formule behoren. Het enige verschil is dat in de tweede formule de kettingregel wordt toegepast.
Voorbeelden van afgeleide van de hyperbolische secans
Nu we de formule kennen voor de afgeleide van de secans hyperbolicus, zullen we verschillende opgeloste oefeningen van dit type trigonometrische afgeleide zien.
voorbeeld 1
![]()
In dit voorbeeld hebben we een andere functie dan x in het hyperbolische secans-argument, dus om deze af te leiden moeten we de kettingregelformule gebruiken.
![]()
Omdat de functie 2x lineair is, is de afgeleide ervan 2. Om de afgeleide te vinden, vervangen we daarom eenvoudigweg de u door 2x en de u’ door 2 in de formule:
![]()
Voorbeeld 2
![]()
De functie van deze oefening is samengesteld, aangezien de secans hyperbolicus een andere functie heeft in zijn argumentatie. We moeten daarom de hyperbolische secansformule met de kettingregel gebruiken om de afleiding te maken:
![]()
De afgeleide van x verhoogd tot 2 geeft 2x, dus de afgeleide van de secans hyperbolicus van x in het kwadraat is:
![]()