Hier vind je de formule voor de afgeleide van de boogcotangens en leggen we met voorbeelden uit hoe je de boogcotangens van een functie kunt afleiden.
arccotangens afgeleide formule
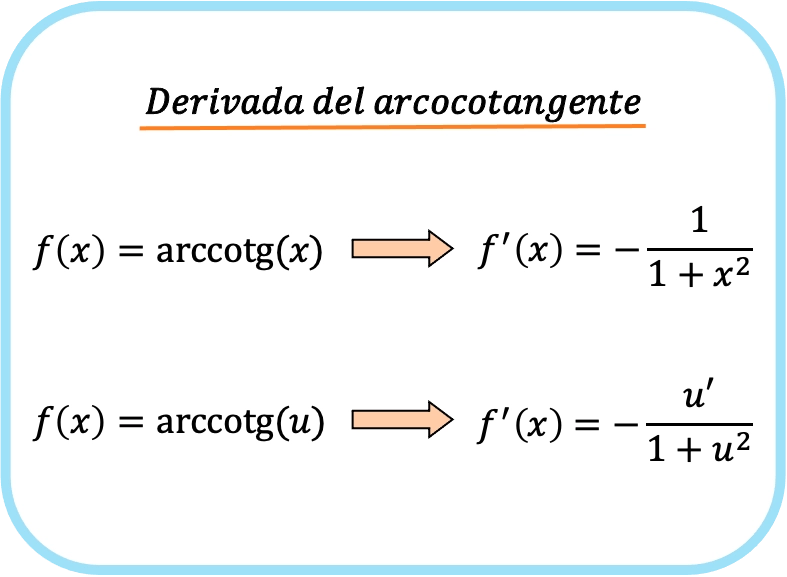
De afgeleide van de boogtangens van x is negatief één gedeeld door één plus x kwadraat.
![]()
Daarom is de afgeleide van de boogcotangens van een functie gelijk aan minus de afgeleide van die functie gedeeld door één plus de kwadratische functie.
![]()
Merk op dat de eerste en tweede formule hetzelfde zijn. Het enige verschil is dat de kettingregel wordt toegepast op de tweede uitdrukking. Als je u vervangt door een x, krijg je in feite de eerste formule, aangezien de afgeleide van de functie x 1 is.
Hoewel de boogcotangens de inverse functie is van de cotangens, zijn hun afgeleiden behoorlijk verschillend. In feite kan de cotangens van een functie op drie manieren worden afgeleid, je kunt ze hier allemaal bekijken:
➤ Zie: formule voor de afgeleide van de cotangens
Voorbeelden van afgeleide van de boogcotangens
Nadat je hebt gezien wat de formule voor de afgeleide van de boogcotangens is, zijn hier twee opgeloste oefeningen van dit type trigonometrische afgeleide. Houd er ook rekening mee dat als u vragen heeft, u uw vraag hieronder in de reacties kunt achterlaten.
voorbeeld 1
In dit voorbeeld zullen we zien hoeveel de afgeleide is van de boogcotangens van de kwadratische functie x 2 .
![]()
In het argument van de boogcotangens hebben we een andere functie dan x, dus moeten we de formule voor de afgeleide van de boogcotangens toepassen met de kettingregel:
![]()
De afgeleide van x verhoogd naar twee is 2x, dus in de teller moeten we 2x zetten en in de noemer de functie van het kwadraatargument:
![]()
Voorbeeld 2
In dit tweede voorbeeld zullen we de boogcotangens van een polynoomfunctie van de derde graad afleiden.
![]()
We gebruiken de arccotangens-afgeleide regel om de afleiding te doen:
![]()
Dus de afgeleide van de boogcotangens van de functie is:
![]()