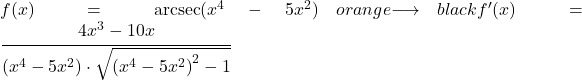Op deze pagina ziet u wat de afgeleide is van de boogsecant (formule). Je vindt opgeloste oefeningen voor afgeleiden van de boogsecant van een functie.
Arcsecant-afgeleide formule
De afgeleide van de boogsecans van x is één over het product van x maal de wortel van x kwadraat min 1.
![]()
Daarom is de afgeleide van de boogsecans van een functie gelijk aan het quotiënt van de afgeleide van die functie gedeeld door de functie maal de wortel van die functie in het kwadraat min één.
![]()
Het is duidelijk dat de tweede formule vergelijkbaar is met de eerste formule, het enige verschil tussen de twee is dat de kettingregel wordt toegepast in de tweede formule.

Hoewel het misschien vreemd lijkt omdat het inverse functies zijn, heeft de afgeleide van de boogsecans niets te maken met de afgeleide van de secans. U kunt de formule voor de afgeleide van de secans bekijken door hier te klikken:
➤ Zie: afgeleide van secans
Voorbeelden van boogsecansderivaat
voorbeeld 1
In dit voorbeeld zullen we zien hoeveel de afgeleide is van de boogsecans van de lineaire functie 7x.
![]()
Om de afgeleide van de boogsecant te vinden, moet je de overeenkomstige formule toepassen, die als volgt luidt:
![]()
De afgeleide van de 7x-functie is 7, dus de afgeleide van de boogsecant van de 7x-functie is:
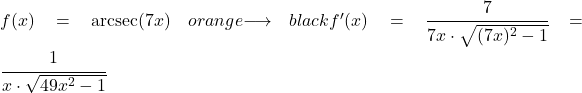
Voorbeeld 2
In dit tweede voorbeeld zullen we de boogsecans van een potentiële functie afleiden.
![]()
Omdat er een andere term dan x in het argument van de boogsecansfunctie voorkomt, moeten we de boogsecansafgeleide regel toepassen met de kettingregel om de gehele functie af te leiden.
![]()
Dus in de teller schrijven we de afgeleide van het argument van de functie, en in de noemer herschrijven we de potentiële functie en vermenigvuldigen we deze met de vierkantswortel van de functie van het argument verheven tot de macht 2 min 1: