In dit artikel leggen we uit hoe je de cosecans van een functie (formule) kunt afleiden. Je vindt er ook stap voor stap opgeloste oefeningen voor de afgeleide van de cosecant. En tot slot zul je de demonstratie van de formule voor dit type trigonometrische afgeleide kunnen zien.
Cosecant-afgeleide formule
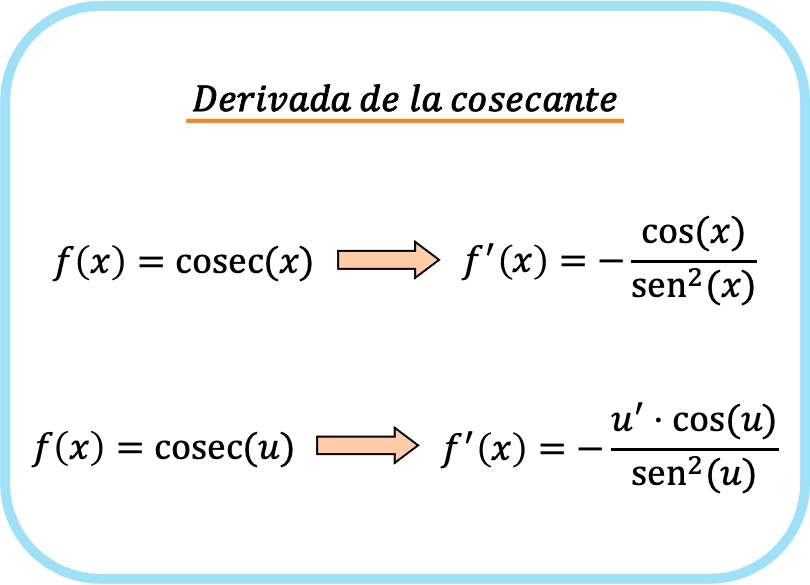
De afgeleide van de cosecans van x is gelijk aan minus het quotiënt van de cosinus van x gedeeld door de vierkante sinus van x.
![]()
Met behulp van goniometrische formules kunnen we ook de afgeleide van de cosecans van x definiëren als minus het product van de cotangens van x maal de cosecans van x.
![]()
En als we de kettingregel toepassen, is de afgeleide van de cosecans van een functie minus het product van de afgeleide van de functie maal de cosinus van de functie, gedeeld door de kwadratische sinus van de functie.
![]()
De formule die wordt gebruikt om de cosecans van een functie af te leiden is daarom als volgt:
Voorbeelden van afgeleide van de cosecans
Nu we hebben gezien wat de formule voor de afgeleide van de cosecans is, zullen we nu verschillende voorbeelden geven. Je kunt dus precies zien hoe de cosecans van een functie wordt afgeleid.
Voorbeeld 1: Afgeleide van de cosecans van 2x
In dit voorbeeld zullen we zien hoeveel de afgeleide is van de cosecans van 2x:
![]()
De cosecans-argumentfunctie verschilt van x, dus we moeten de cosecans-afgeleide regel gebruiken met de kettingregel.
![]()
Dus om de afgeleide van deze trigonometrische functie te vinden, vervangt u eenvoudigweg de waarden in de vorige formule: in het cosinus- en sinusargument plaatsen we 2x, en u’ komt overeen met de afgeleide van 2x, dat wil zeggen 2:
![]()
Voorbeeld 2: Afgeleide van de cosecans van x kwadraat
In deze oefening zullen we zien hoeveel de afgeleide is van de cosecans van x in het kwadraat:
![]()
Logischerwijs wordt de afgeleide van deze trigonometrische functie opgelost met behulp van de formule voor de afgeleide van de cosecans:
![]()
De afgeleide van x in het kwadraat geeft 2x, dus de afgeleide van de cosecans van x tot de macht van twee is:
![]()
Voorbeeld 3: Afgeleide van de derde machtssecans van een exponentiële functie
![]()
Wat het argument van de functie ook is, de regel voor de afgeleide van de cosecans van een functie is:
![]()
Maar in dit geval hebben we een samengestelde functie, omdat de cosecans wordt verhoogd tot drie en bovendien is er in zijn argumentatie een exponentiële functie. Om de hele functie te differentiëren, moeten we de kettingregel dus verschillende keren toepassen:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9ac2ce49dfcba1b7f27696dba0a2decb_l3.png)
Opgeloste problemen van de afgeleide van de cosecant
Leid de volgende cosecante functies af:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-32dde68d2a11ef6a05d483b26f0a98ef_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b2bea25dae467cefdcc1bd48e8d9bc88_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-eb70e1d7b6f2ce2636934b235904861f_l3.png)
Bewijs van de formule voor de afgeleide van de cosecant
Vervolgens zullen we de formule demonstreren voor de afgeleide van de cosecans. In tegenstelling tot andere demonstraties zullen we in dit geval niet de limiet gebruiken die een afgeleide definieert, maar zullen we uitgaan van de wiskundige definitie van de cosecans.
Algebraïsch is de cosecante trigonometrische functie de multiplicatieve inverse van sinus:
![]()
We kunnen daarom de afgeleide van de cosecans nemen met behulp van de quotiëntregel:
![]()
![]()
Zoals je kunt zien, komen we alleen door de regel voor de afgeleide van een deling toe te passen tot de formule voor de afgeleide van de cosecans. En aangezien de afgeleide van een quotiënt al bewezen is (je kunt het zien in de volgende link), is de cosecante afgeleide regel ook bewezen.