Hyperbolisch arcsinusderivaat

Hier vindt u wat de afgeleide is van de hyperbolische boogsinus (formule). Bovendien zul je verschillende oefeningen kunnen zien die zijn opgelost op de afgeleiden van de hyperbolische boogsinus van een functie. Ten slotte laten we u de formule zien voor de afgeleide van dit type trigonometrische functie.

Hyperbolische arcsine-afgeleide formule

De afgeleide van de hyperbolische boogsinus van x is één gedeeld door de wortel van x in het kwadraat plus 1.

f(x)=\text{arcsenh}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{x^2+1}}

Dus de afgeleide van de hyperbolische boogsinus van een functie is gelijk aan het quotiënt van de afgeleide van die functie gedeeld door de vierkantswortel van die functie in het kwadraat plus één.

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

De tweede formule lijkt op de eerste, maar past de kettingregel toe. Dat wil zeggen dat met de eerste formule alleen de hyperbolische boogsinus van xy kan worden afgeleid, terwijl met de tweede formule de hyperbolische boogsinus van elke functie kan worden afgeleid.

afgeleid van de hyperbolische boogsinus

Houd er rekening mee dat hyperbolische boogsinus de inverse functie is van hyperbolische sinus, waarvan je de afgeleide hier kunt zien:

➤ Zie: formule voor de afgeleide van de hyperbolische sinus

Voorbeelden van het hyperbolische arcsinederivaat

voorbeeld 1

f(x)=\text{arcsenh}(3x)

Om de afgeleide van de boogsinusfunctie op te lossen, gebruiken we de bovenstaande formule:

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

De afgeleide van 3x is 3, dus een 3 komt in de teller. En in de noemer hoeven we alleen maar de wortel van 3x kwadraat plus 1 te zetten:

f(x)=\text{arcsenh}(3x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3}{\sqrt{(3x)^2+1}}=\cfrac{3}{\sqrt{9x^2+1}}

Voorbeeld 2

f(x)=\text{arcsenh}(x^3)

Om de hyperbolische boogsinus van de functie x in de derde macht af te leiden, moeten we dezelfde formule toepassen:

f(x)=\text{arcsenh}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{u^2+1}}

De afgeleide van x in de derde macht is 3x 2 , dus de afgeleide van de hyperbolische boogsinus van x verhoogd tot 3 wordt:

f(x)=\text{arcsenh}(x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3x^2}{\sqrt{\left(x^3\right)^2+1}}=\cfrac{3x^2}{\sqrt{x^6+1}}

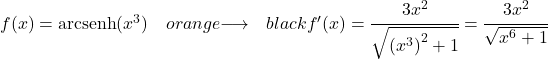
Bewijs van het hyperbolische boogsinusderivaat

We zullen de formule demonstreren voor de afgeleide van de hyperbolische boogsinus:

y=\text{arcsenh}(x)

Eerst transformeren we de hyperbolische boogsinus in een hyperbolische sinus:

x=\text{senh}(y)

Van beide kanten van de gelijkheid leiden we het volgende af:

1=\text{cosh}(y)\cdot y'

Wij zuiveren u:

y'=\cfrac{1}{\text{cosh}(y)}

Vervolgens passen we de trigonometrische identiteit toe die de hyperbolische sinus en de hyperbolische cosinus verbindt:

\text{cosh}^2(y)-\text{senh}^2(y)=1 \ \longrightarrow \ \text{cosh}(y)=\sqrt{1+\text{senh}^2(y)}

y'=\cfrac{1}{\sqrt{1+\text{senh}^2(y)}}

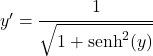
Maar hierboven hebben we afgeleid dat x overeenkomt met de hyperbolische sinus van y, dus de vergelijking blijft:

y'=\cfrac{1}{\sqrt{1+x^2}}

Zoals je kunt zien, hebben we door deze stappen toe te passen de formule voor de afgeleide van de hyperbolische boogsinus verkregen, en daarom is deze bewezen.

Gelijkwaardige producten

Laat een reactie achter

Je e-mailadres wordt niet gepubliceerd. Vereiste velden zijn gemarkeerd met *

Scroll naar boven