Hier vindt u wat de afgeleide is van de hyperbolische tangens van een functie. Bovendien zult u verschillende opgeloste voorbeelden van afgeleiden van hyperbolische raaklijnen kunnen zien. En tot slot laten we u de formule zien voor de afgeleide van de hyperbolische tangens.
Formule voor de afgeleide van de hyperbolische tangens
De afgeleide van de hyperbolische tangens van x is gelijk aan 1 gedeeld door het kwadraat van de hyperbolische cosinus van x. De afgeleide van de raaklijn van x is ook gelijk aan het kwadraat van de hyperbolische secans van x, en 1 minus het kwadraat van de hyperbolische raaklijn van x.
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tanh}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=\text{sech}^2(x)=1-\text{tanh}^2(x)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9a7c392afdb3bbf504e167e15fb2fee6_l3.png)
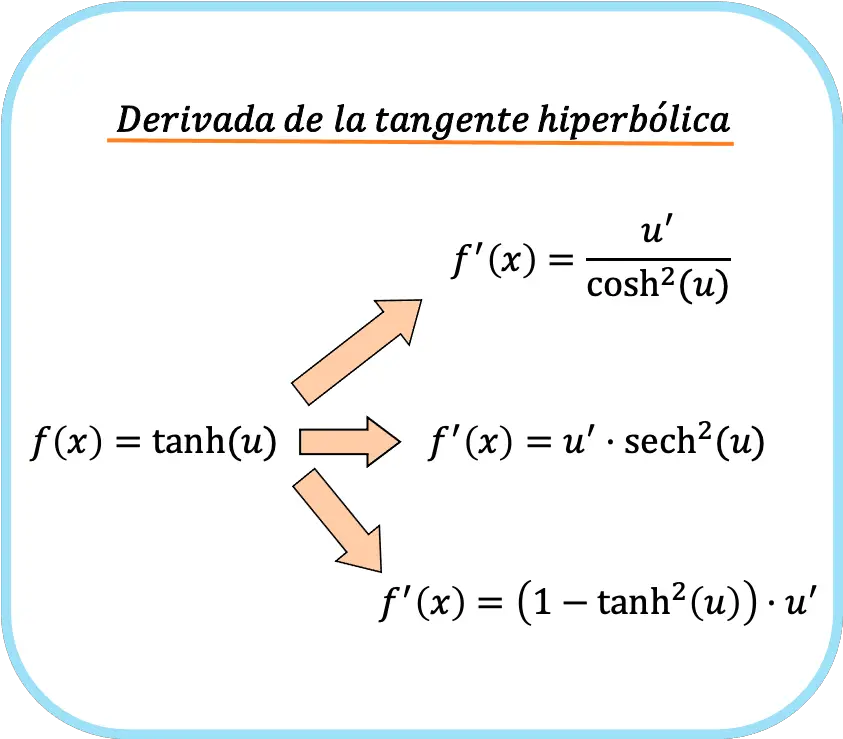
Aan de andere kant, als we in het functieargument een andere functie dan x hebben, moeten we de kettingregel toepassen. En dan zijn de drie formules voor de afgeleide van de hyperbolische tangens:
![Rendered by QuickLaTeX.com \begin{array}{c}f(x)=\text{tanh}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=\cfrac{u'}{\text{cosh}^2(u)}=\text{sech}^2(u)\cdot u'=\left(1-\text{tanh}^2(u)\right)\cdot u'\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b5ee01c6675067b20f71ea8ac4efcfe5_l3.png)
Dit betekent niet dat we elke keer dat we de hyperbolische tangens afleiden, alle drie de formules moeten gebruiken, maar dat we elk van deze formules kunnen gebruiken om deze af te leiden. Afhankelijk van de functie van het hyperbolische tangens-argument is het dus beter om de ene of de andere formule te gebruiken. Hieronder staan enkele voorbeelden waarin u kunt zien hoe de hyperbolische tangens van een functie wordt afgeleid.
De afgeleide van de hyperbolische raaklijn is bijna identiek aan de afgeleide van de raaklijn, maar heeft een klein detail waardoor ze totaal verschillend zijn. Wat het verschil is, kun je zien via de volgende link:
➤ Zie: raaklijnafgeleide formule
Voorbeelden van afgeleide van de hyperbolische tangens
Nadat je hebt gezien wat de formule voor de afgeleide van de hyperbolische tangens is, volgen hier enkele opgeloste voorbeelden van afgeleiden van dit type trigonometrische functies, zodat je volledig begrijpt hoe je de hyperbolische tangens kunt afleiden.
Voorbeeld 1: Afgeleide van de hyperbolische tangens van 2x
![]()
Om de hyperbolische tangens in dit voorbeeld af te leiden, gebruiken we de hyperbolische cosinusformule, hoewel je natuurlijk kunt gebruiken wat je maar wilt.
![]()
We weten dat de afgeleide van 2x 2 is, dus de afgeleide van de gehele functie is:
![]()
Voorbeeld 2: Afgeleide van de hyperbolische tangens van x kwadraat
![]()
De regel voor de afgeleide van de hyperbolische tangens van een functie is:
![]()
Aan de ene kant differentiëren we de functie van het argument x 2 , wat 2x oplevert, en vervolgens lossen we de afgeleide van de gehele functie op met behulp van de formule:
![]()
Voorbeeld 3: Afgeleide van de hyperbolische tangens in blokjes
![]()
In dit geval moeten we de hyperbolische tangens afleiden van een functie die bovendien tot een macht wordt verheven. We moeten dus de formule gebruiken voor de afgeleide van een potentiële functie, de regel voor de afgeleide van de hyperbolische tangens en de kettingregel:
![]()
Bewijs van de afgeleide van de raaklijn
In deze sectie zullen we de formule demonstreren voor de afgeleide van de hyperbolische tangens. En hiervoor gaan we uit van de trigonometrische identiteit die de drie hyperbolische trigonometrische verhoudingen met elkaar verbindt:
![]()
➤ Opmerking: om het bewijs te begrijpen, moet je weten wat de afgeleide is van de hyperbolische sinus en wat de afgeleide is van de hyperbolische cosinus . Daarom raden wij u aan de gelinkte pagina’s te bezoeken voordat u verdergaat.
Laten we nu de formule voor de afgeleide van een quotiënt toepassen:
![]()
![]()
![]()
We verminderen de uitdrukking van de teller van de breuk met behulp van de volgende formule:
![]()
![]()
Zoals je kunt zien, komt de vorige gelijkheid overeen met de eerste formule voor de afgeleide van de hyperbolische tangens. Op dezelfde manier is de hyperbolische secans de multiplicatieve inverse van de hyperbolische cosinus, dus wordt ook de tweede formule afgeleid:
![]()
Ten slotte kunnen we tot de derde regel van de afgeleide van de hyperbolische tangens komen door de breuk uit de vorige stap om te zetten in een aftrekking van breuken:
![]()
![]()
![]()