Afgeleide van boogcosinus

Hier leggen we uit hoe je de arccosinus van een functie kunt afleiden. Daarnaast vind je voorbeelden van afgeleiden van de boogcosinus en kun je oefenen met stap voor stap opgeloste oefeningen. Ten slotte laten we u het bewijs zien van de arccosine-afgeleide formule.

Wat is de afgeleide van boogcosinus?

De afgeleide van de arccosinus van x is negatief één over de vierkantswortel van één minus x kwadraat.

$f(x)=\text{arccos}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{1}{\sqrt{1-x^2}}$

Daarom is de afgeleide van de arccosinus van een functie gelijk aan minus het quotiënt van de afgeleide van die functie gedeeld door de vierkantswortel van één minus het kwadraat van die functie.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

In feite wordt de eerste formule verkregen door x in de tweede formule te vervangen door u. Samenvattend: de formule voor de afgeleide van de inverse cosinus is:

Zoals je kunt zien, is de formule voor de afgeleide van arccosinus hetzelfde als de afgeleide van arcsinus , maar met een negatief ervoor.

Voorbeelden van de boogcosinusderivaat

Gegeven de formule voor de afgeleide van de arccosinusfunctie, zullen we nu verschillende voorbeelden van dit soort trigonometrische derivaten analyseren. Op deze manier wordt het gemakkelijker voor u om te begrijpen hoe de boogcosinus van een functie wordt afgeleid.

Voorbeeld 1: Afgeleide van de boogcosinus van 2x

$f(x)=\text{arccos}(2x)$

Om de afgeleide van de boogcosinus op te lossen, gebruiken we de formule:

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

De afgeleide van 2x is 2, dus de boogcosinusafgeleide van 2x is negatief 2 over de wortel één minus 2x kwadraat:

$f(x)=\text{arccos}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\sqrt{1-(2x)^2}}=-\cfrac{2}{\sqrt{1-4x^2}}$

Voorbeeld 2: Afgeleide van de boogcosinus van x kwadraat

$f(x)=\text{arccos}(x^2)$

We passen de arccosine-afgeleide formule toe met de kettingregel om de afgeleide te berekenen:

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

Omdat de afgeleide van de functie x ² 2x is, is de afgeleide van de boogcosinus van x tot de macht van 2:

$f(x)=\text{arccos}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=-\cfrac{2x}{\sqrt{1-x^4}}$

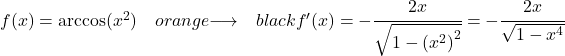
Voorbeeld 3: Afgeleide van de arccosinus van een logaritme

$f(x)=\text{arccos}\bigl(\ln (x)\bigr)$

De functie in dit voorbeeld is een functie die is samengesteld uit een arccosinus en een natuurlijke logaritme, dus we moeten de kettingregel gebruiken om deze af te leiden.

$f(x)=\text{arccos}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\sqrt{1-u^2}}$

De afgeleide van de natuurlijke logaritme is één gedeeld door x, daarom is de afgeleide van de gehele functie:

$f(x)=\text{arccos}\bigl(\ln (x)\bigr) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\cfrac{1}{x}}{\sqrt{1-\left(\ln(x)\right)^2}}=\cfrac{1}{x\sqrt{1-\ln^2(x)}}$

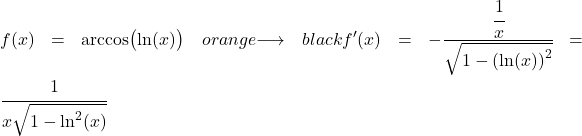
Arccosinederivaat loste problemen op

Leid de volgende arccosinusfuncties af:

$\text{A) }f(x)=\text{arccos}(7x)$

$\text{B) }f(x)=\text{arccos}(x^3+6x)$

$\text{C) }f(x)=\text{arccos}^3\left(e^{3x}\right)$

$\text{D) }f(x)=\text{arccos}\left(\log_3(x^3)\right)$

$\text{E) }f(x)=\text{arccos}\left(\sqrt{4x}\right)$

zie oplossing

$\text{A) }f'(x)=-\cfrac{7}{\sqrt{1-(7x)^2}}=-\cfrac{7}{\sqrt{1-49x^2}}$

$\text{B) }f'(x)=-\cfrac{3x^2+6}{\sqrt{1-(x^3+6x)^2}}$

$\begin{aligned}\text{C) }\displaystyle f'(x)&=3\text{arccos}^2\left(e^{3x}\right)\cdot \left(-\frac{3e^{3x}}{\sqrt{1-\left(e^{3x}\right)^2}}\right)\\[1.5ex] &=-\cfrac{9\text{arccos}^2\left(e^{3x}\right)\cdot e^{3x}}{\sqrt{1-e^{6x}}}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)&=-\cfrac{1}{\sqrt{1-\left(\log_3(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 3}\\[1.5ex] &=-\cfrac{1}{x\cdot \ln 3\cdot \sqrt{1-\log_3^2(3x)}} \end{aligned}$

$\begin{aligned}\text{E) } f'(x)& =-\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=-\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=-\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}$