Afgeleid van een wortel: Mathority

Hier leggen we uit hoe je de afgeleide van een wortel (of een radicaalfunctie) kunt nemen. Je vindt de formule voor het delen van wortels en oefeningen stap voor stap opgelost voor afgeleiden van wortels.

Formule voor de afgeleide van een wortel

De afgeleide van een wortel, of irrationele functie, is gelijk aan de afgeleide van de wortel (uitdrukking onder de wortel) gedeeld door het product van de index van de wortel maal dezelfde wortel, waarbij 1 wordt afgetrokken van de exponent van de wortel.

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

Als de wortelradicand echter slechts een x is, worden de formules eenvoudiger. De wortelafgeleide van x is daarom de volgende:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Kortom, er zijn twee formules voor het afleiden van een wortel: de eerste die altijd kan worden gebruikt en de tweede die alleen kan worden gebruikt als het wortelteken x is.

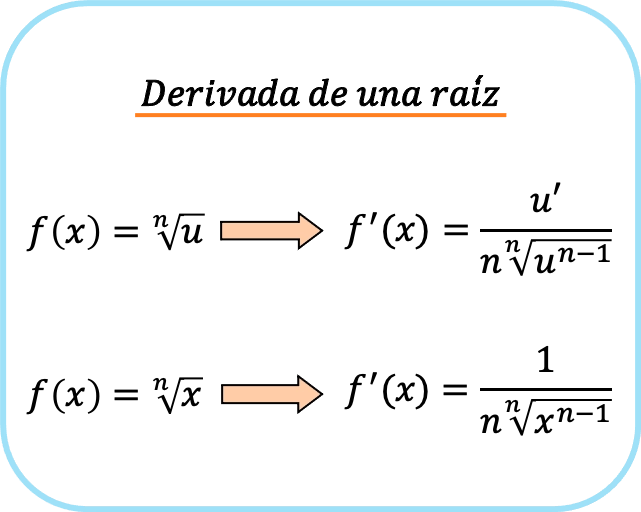
Als je goed kijkt, is de term in de teller van de breuk degene die het resultaat is van het toepassen van de kettingregel bij het nemen van de afgeleide van de wortel. Dit is de reden waarom wanneer het wortelteken x is, 1 in de noemer verschijnt, aangezien dit de afgeleide is van x.

Voorbeelden van wortelderivaten

Gegeven de formule voor de afgeleide van een radicaalfunctie, leggen we hieronder verschillende voorbeelden van dit type afgeleide uit, zodat je begrijpt hoe je de afgeleide van een wortel moet nemen.

Voorbeeld 1: Afgeleide van een vierkantswortel

We zullen dan zien wat de afgeleide van een vierkantswortel is:

$f(x)=\sqrt{x}$

In dit geval is de uitdrukking binnen de wortel slechts een x, dus we kunnen de volgende formule gebruiken:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Dus de afgeleide van een vierkantswortel is gelijk aan 1 gedeeld door het product van 2 keer de vierkantswortel van x:

$f(x)=\sqrt{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{2\sqrt{x^{2-1}}}=\cfrac{1}{2\sqrt{x}}$

Voorbeeld 2: Afgeleide van een derdemachtswortel

$f(x)=\sqrt[3]{x}$

In dit voorbeeld is de uitdrukking onder de wortel een x, dus we kunnen de volgende formule toepassen:

$f(x)=\sqrt[n]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{n\sqrt[n]{x^{n-1}}}$

Dus de afgeleide van een derdemachtswortel is gelijk aan 1 gedeeld door 3 keer de derdemachtswortel van x in het kwadraat:

$f(x)=\sqrt[3]{x}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{1}{3\sqrt[3]{x^{3-1}}}=\cfrac{1}{3\sqrt[3]{x^2}}$

Voorbeeld 3: Afgeleide van een vierde wortel

$f(x)=\sqrt[4]{7x-2}$

Nu hebben we geen x onder het wortelteken, maar wel een complexere algebraïsche uitdrukking. Daarom moeten we de algemene formule gebruiken voor de afgeleide van een wortel:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

De uitdrukking onder het radicaal is een eerstegraadsfunctie, dus de afgeleide ervan is 7. De afgeleide van de gehele functie is dus:

$f(x)=\sqrt[4]{7x-2}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{7}{4\sqrt[4]{(7x-2)^3}}$

Voorbeeld 4: Afleiding van de ene wortel naar de andere

$f(x)=\sqrt{x^2+\sqrt[3]{x^4-5}}$

Om de afgeleide van deze wortel, bestaande uit een andere wortel, op te lossen, moeten we de volgende formule toepassen:

$f(x)=\sqrt[n]{u}\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=\cfrac{u'}{n\sqrt[n]{u^{n-1}}}$

In dit geval moet u twee keer achter elkaar dezelfde formule gebruiken om de afgeleide te berekenen:

$\begin{aligned}f'(x)& =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot\left(x^2+\sqrt[3]{x^4-5}\right)' \\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot (x^4-5)'\right)\\[3ex]&\displaystyle =\cfrac{1}{2\sqrt{x^2+\sqrt[3]{x^4-5}}}\cdot \left(2x+\frac{1}{ 3\sqrt[3]{(x^4-5)^2}}\cdot 4x^3\right)\end{aligned}$

Opgeloste problemen van de afgeleide van een wortel

Bereken de afgeleiden van de volgende wortels:

$\text{A) } f(x)=\sqrt[5]{x}$

$\text{B) } f(x)=\sqrt[3]{x^4}$

$\text{C) } f(x)=\sqrt{x^2-4x+9}$

$\text{D) } f(x)=\sqrt[4]{x^9+5x^4-2x}$

$\text{E) } f(x)=\sqrt[5]{3(x^2-1)^4}$

$\text{F) } f(x)=\sqrt[6]{x^2+4(5x^3-8x)^2}$

zie oplossing

$\text{A) } f'(x)=\cfrac{1}{5\sqrt[5]{x^4}}$

$\text{B) } f'(x)=\cfrac{4x^3}{3\sqrt[3]{\left(x^4\right)^2}}= \cfrac{4x^3}{3\sqrt[3]{x^8}}$

$\text{C) } f'(x)=\cfrac{2x-4}{2\sqrt{x^2-4x+9}}$

$\text{D) } f'(x)=\cfrac{9x^8+20x^3-2}{4\sqrt[4]{\left(x^9+5x^4-2x\right)^3}}$

$\text{E) } f'(x)=\cfrac{3\cdot 4 \cdot (x^2-1)^3\cdot 2x}{5\sqrt[5]{\left(3\left(x^2-1\right)^4\right)^4}}=\cfrac{24x(x^2-1)^3}{5\sqrt[5]{81\left(x^2-1\right)^{16}}}$

$\text{F) } f'(x)=\cfrac{2x+2\cdot 4(5x^3-8x)\cdot (15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}=\cfrac{2x+8(5x^3-8x)(15x^2-8)}{6\sqrt[6]{\left(x^2+4(5x^3-8x)^2\right)^5}}$

Formule voor de afgeleide van een wortel

Voorbeelden van wortelderivaten

Voorbeeld 1: Afgeleide van een vierkantswortel

Voorbeeld 2: Afgeleide van een derdemachtswortel

Voorbeeld 3: Afgeleide van een vierde wortel

Voorbeeld 4: Afleiding van de ene wortel naar de andere

Opgeloste problemen van de afgeleide van een wortel

Laat een reactie achter Reactie annuleren