Afgeleide van een lineaire functie

In dit artikel laten we zien hoeveel de afgeleide is van een lineaire functie. Daarnaast lossen we verschillende voorbeelden op van afgeleiden van lineaire functies en demonstreren we de formule voor dit type afgeleide. Je vindt er zelfs opgeloste oefeningen over de afgeleiden van lineaire functies.

Wat is de afgeleide van een lineaire functie?

De afgeleide van een lineaire functie is de coëfficiënt van de eerstegraadsterm , dat wil zeggen dat de afgeleide van een lineaire functie f(x)=Ax+B gelijk is aan A.

$f(x)=Ax+B\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=A$

De onafhankelijke term wordt uit de afgeleide verwijderd omdat de afgeleide van een constante nul is. En aan de andere kant is de afgeleide van een term van de eerste graad de coëfficiënt van die term. Daarom is de afgeleide van de som van deze twee soorten functies de coëfficiënt van de lineaire term.

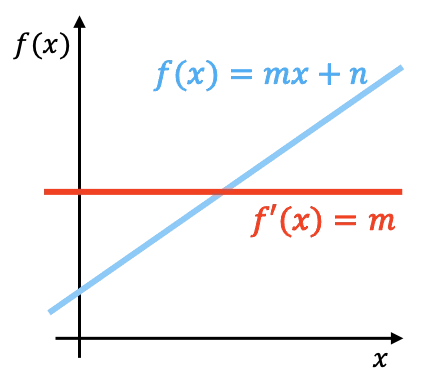
Geometrisch gezien is de afgeleide van een lineaire functie de helling van die functie. In de bovenstaande grafiek ziet u een lineaire functie met zijn afgeleide.

Voorbeelden van afgeleiden van lineaire functies

Gegeven de definitie van de afgeleide van een lineaire functie, zullen we verschillende voorbeelden van lineaire functies berekenen om het begrip van het concept te voltooien:

$\begin{array}{c}f(x)=3x+1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x-4\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}$

Houd er rekening mee dat de afgeleide van de lineaire functie altijd het getal is dat bij de variabele x hoort als de functie geen onafhankelijke term heeft, of met andere woorden, als deze slechts één term van de eerste graad heeft. Bijvoorbeeld:

$f(x)=8x\quad\longrightarrow\quad f'(x)=8$

Daarom is de afgeleide van een lineaire functie een functie zonder onafhankelijke variabele, een eenvoudig getal.

Bewijs van de afgeleide van een lineaire functie

Vervolgens zullen we de formule demonstreren voor de afgeleide van een lineaire functie.

Laat f een willekeurige lineaire functie zijn :

$f(x)=Ax+B$

De formule voor het berekenen van de afgeleide van een functie in een punt is:

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$

Dus als we de vorige limiet voor een lineaire functie berekenen, krijgen we:

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}=\frac{A(a+h)+B-(A\cdot a+B)}{h}$

We lossen de haakjes op:

$\displaystyle f'(a)=\frac{Aa+Ah+B-Aa-B}{h}$

We werken in de teller:

$\displaystyle f'(a)=\frac{Ah}{h}$

En tot slot vereenvoudigen we de breuk:

$\displaystyle f'(a)=A$

Concluderend: de afgeleide van een lineaire functie is op elk punt gelijk aan de coëfficiënt van de eerstegraadsterm. Zo wordt de formule voor de afgeleide van een lineaire functie afgeleid.

Opgeloste problemen van afgeleiden van lineaire functies

Bereken de afgeleiden van de volgende lineaire functies:

$\text{A)}\ f(x)=2x-25$

$\text{B)}\ f(x)=x+3$

$\text{C)}\ f(x)=-9x-1$

$\text{D)}\ f(x)=\cfrac{1}{2}x+7$

$\text{E)}\ f(x)=5x$

$\text{F)}\ f(x)=\sqrt{7}x+\frac{3}{4}$

zie oplossing

Om een lineaire functie af te leiden, elimineert u eenvoudigweg de constante term en de variabele uit de functie, zodat alleen de coëfficiënt van de lineaire term overblijft. Nog:

$\text{A)}\ f'(x)=2$