Hier vind je wat de verticale asymptoten van een functie zijn (met voorbeelden). Ook leggen we uit hoe je de verticale asymptoten van een functie kunt vinden en daarnaast kun je oefenen met stap voor stap opgeloste oefeningen.
Wat is een verticale asymptoot?
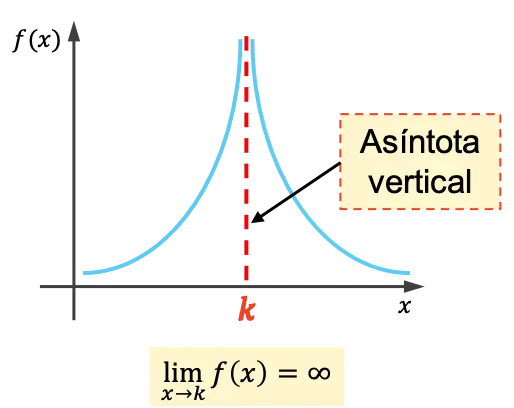
Een verticale asymptoot van een functie is een verticale lijn waarvan de grafiek oneindig nadert zonder deze ooit te kruisen. Daarom is de vergelijking voor een verticale asymptoot x=k , waarbij k de waarde van de verticale asymptoot is.
Dat wil zeggen, k is een verticale asymptoot als de limiet van de functie wanneer x k nadert oneindig is.
Hoe de verticale asymptoot van een functie te berekenen
Om de verticale asymptoot van een functie te berekenen, moeten de volgende stappen worden gevolgd:
- Zoek het domein van de functie. Als alle punten zich in het domein bevinden, heeft de functie geen verticale asymptoten.
- Bereken de limiet van de functie op punten die niet in het domein liggen.
- De verticale asymptoten van de functie zullen alle waarden zijn waarin de limiet oneindig geeft.
Merk op dat een functie meer dan één verticale asymptoot kan hebben. De grafiek van de raaklijnfunctie heeft bijvoorbeeld oneindig veel verticale asymptoten.
➤ Zie: kenmerken van de raaklijnfunctie
Voorbeeld van verticale asymptoot
Als voorbeeld zullen we alle asymptoten van de volgende rationale functie vinden, zodat je kunt zien hoe het werkt:
![]()
Over het algemeen behoren punten met verticale asymptoten niet tot het domein van de functie. Daarom zullen we eerst het domein van de functie berekenen.
Het is een rationale functie, dus we kijken wanneer de noemer verdwijnt om de punten te bepalen die niet tot het domein behoren:
![]()
![]()
Daarom bestaat het domein van de functie uit alle reële getallen behalve x=2:
![]()
Dus x=2 zou een verticale asymptoot van de functie kunnen zijn. Om dit te verifiëren, moeten we op dit punt de limiet van de functie berekenen:
![]()
In dit geval hebben we de onbepaaldheid van een getal tussen nul verkregen en daarom moeten we, om de limiet op te lossen, de laterale limieten berekenen om te weten of deze plus oneindig, minus oneindig is of dat de limiet niet bestaat. Wanneer we echter verticale asymptoten berekenen, hoeven we de laterale grenzen niet uit te voeren, maar het verkrijgen van deze onbepaaldheid is voldoende om te zeggen dat het een verticale asymptoot is.
Kortom, aangezien de limiet van de functie wanneer x 2 nadert oneindigheid oplevert, is x = 2 een verticale asymptoot.
Hieronder ziet u de functie grafisch weergegeven. Zoals je kunt zien, komt hij heel dicht bij de x=2-lijn (zowel van links als van rechts), maar hij snijdt hem nooit omdat hij een verticale asymptoot is:

Bovendien kunnen we uit de grafiek de laterale grenzen van de functie op het punt x = 2 afleiden:
![]()
Opgeloste problemen van verticale asymptoten
Oefening 1
Bereken de verticale asymptoot van de volgende rationale functie:
![]()
Er bestaat geen formule om de verticale asymptoten van een functie te berekenen, maar je moet het domein van de functie vinden en kijken op welke punten waar de functie niet gedefinieerd is, de limiet oneindig oplevert.
Daarom stellen we de noemer van de rationale functie gelijk aan 0 om de punten te vinden die niet tot het domein behoren:
![]()
![]()
![]()
Het domein van de functie bestaat dus uit alle reële getallen behalve x=1/2:
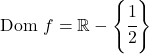
Dus x=1/2 zou een verticale asymptoot kunnen zijn. Om dit te controleren, berekenen we op dit punt de limiet van de functie:
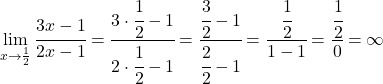
Dus x=1/2 is een verticale asymptoot , aangezien de limiet van de functie op dit punt oneindigheid oplevert.
Oefening 2
Vind alle verticale asymptoten van de volgende fractionele functie:
![]()
Eerst stellen we de noemer van de breuk gelijk aan nul om te zien welke waarden niet in het domein van de functie liggen:
![]()
We lossen de onvolledige kwadratische vergelijking op:
![]()
![]()
Het domein van de rationale functie is daarom:
![]()
Om te bepalen welke van deze twee waarden verticale asymptoten zijn, lossen we dus de limiet van de functie op elk punt op:
![]()
![]()
De twee limieten geven oneindigheid aan, dus x=3 en x=-3 zijn de twee verticale asymptoten van de probleemfunctie .
Oefening 3
Zoek, als je dat hebt, alle verticale asymptoten van de volgende rationale functie:
![]()
➤ Zie: nul tussen nul onbepaaldheid
Eerst lossen we de kwadratische noemervergelijking op om de waarden te vinden die de noemer van de breuk opheffen:
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle x&=\cfrac{-b\pm\sqrt{b^2-4ac}}{2a}=\cfrac{-2\pm\sqrt{2^2-4\cdot1\cdot(-3)}}{2\cdot1}=\\[3ex]\displaystyle &=\cfrac{-2\pm\sqrt{16}}{2}=\cfrac{-2\pm 4}{2}=\begin{cases}\cfrac{-2+4}{2}=1\\[3ex]\cfrac{-2-4}{2}=-3\end{cases}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9b2170358d5d1719077695aba5afa02e_l3.png)
Het domein van de functie is dus:
![]()
We berekenen dus eerst de limiet van de functie op x=1:
![]()
En aan de andere kant lossen we de limiet van de functie op wanneer x naar -3 neigt:
![Rendered by QuickLaTeX.com \begin{array}{l}\displaystyle\lim_{x \to -3}\frac{x+3}{x^2+2x-3}=\frac{-3+3}{(-3)^2+2\cdot(-3)-3}=\frac{0}{0}=\\[3ex]\displaystyle =\lim_{x \to -3}\frac{\cancel{x+3}}{(x-1)\cancel{(x+3)}}=\lim_{x \to -3}\frac{1}{x-1}=\frac{1}{-3-1}=-\frac{1}{4}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f0e96a48986cd110e04058e3545290a0_l3.png)
De vorige limiet geeft de onbepaalde vorm nul tussen nul, dus om deze op te lossen moeten we de polynomen ontbinden in factoren. Als je twijfelt over hoe we de limiet hebben opgelost, kun je de volledige uitleg over hoe je dit soort onbepaaldheid kunt oplossen bekijken in de link naar de oefenverklaring.
In dit geval geeft alleen de limiet van de functie op het punt x=1 oneindigheid, dus x=1 is de enige verticale asymptoot van de functie .