Laterale grenzen - Mathority

In dit artikel leggen we uit wat de laterale limiet van een functie is (met voorbeelden). We leren u ook hoe u de linker- en rechterlaterale grenzen van een functie kunt berekenen, zowel grafisch als numeriek. Bovendien kunt u trainen met oefeningen die stapsgewijs worden opgelost met de laterale limieten.

Wat zijn de laterale grenzen?

Laterale grenzen van een functie op een punt bestuderen het gedrag van de functie rond dat punt. Er is de linker laterale limiet en de rechter laterale limiet, die respectievelijk de waarde van de functie links en rechts van het beschouwde punt analyseert.

Laterale grenzen links en rechts

Zoals we bij de definitie van laterale grenzen hebben gezien, zijn er twee typen: linker laterale grenzen en rechter laterale grenzen.

De linkerlimiet van de functie wordt uitgedrukt door een minteken op het punt waar de limiet wordt geanalyseerd, en aan de andere kant wordt de rechterlimiet aangegeven door het plusteken.

Laterale grens aan de linkerkant

$\displaystyle\lim_{x\to a^{\color{orange}\bm{-}\color{black}}}f(x)$

Laterale grens aan de rechterkant

$\displaystyle\lim_{x\to a^{\color{orange}\bm{+}\color{black}}}f(x)$

Bekijk het volgende voorbeeld om de betekenis van laterale limieten beter te begrijpen:

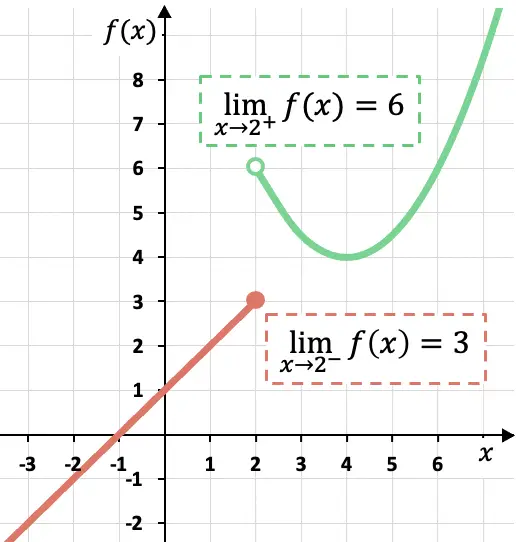
Zoals u kunt zien in de grafische weergave van deze stuksgewijze functie, zijn de laterale grenzen afhankelijk van de zijde waarop ze worden berekend.

In dit geval benadert de functie 3 terwijl x 2 van links benadert, aangezien de functie waarden aanneemt die dichter bij 3 liggen als x x=2 van links nadert.

Aan de andere kant is de laterale limiet van de functie op x=2 bij de lijn 6 waard. Want als we het punt x=2 benaderen bij zijn lijn, neemt de functie waarden steeds dichter bij f(x)= 6.

Aan de andere kant moet u weten dat laterale limieten dezelfde eigenschappen hebben als gewone limieten. In de volgende link kun je zien wat de grenseigenschappen zijn:

➤ Zie: grenseigenschappen

gelijke laterale grenzen

We hebben zojuist een voorbeeld gezien waarin de zijgrenzen van een functie verschillend zijn, maar… wat gebeurt er als de zijgrenzen hetzelfde zijn?

Als beide laterale grenzen van een functie op een punt bestaan en gelijk zijn , bestaat de limiet van de functie op dat punt en is het resultaat van de limiet de waarde van de laterale grenzen.

Met andere woorden, om de limiet van een functie op een bepaald punt te laten bestaan, moet aan de volgende voorwaarde worden voldaan:

$\displaystyle\lim_{x\to a^-}f(x)=\lim_{x\to a^+}f(x)=L \ \iff \ \lim_{x\to a}f(x)=L$

Als de laterale grenzen van een functie op een punt verschillend zijn, bestaat de limiet van de functie op dat punt dus niet.

Ook dat de limiet van een functie op een punt bestaat, is een essentiële voorwaarde om op een punt een continue functie te kunnen zijn.

Laten we een voorbeeld oplossen om het concept van laterale limieten beter te begrijpen:

De laterale grenzen op het punt x=-2 van de grafisch weergegeven functie vallen samen, aangezien de waarde van de functie naar 3 neigt, ongeacht of we x=-2 van links of van rechts benaderen. Daarom is de limiet van de functie bij x=-2 gelijk aan 3.

$\displaystyle\lim_{x\to -2^-}f(x)=\lim_{x\to -2^+}f(x)=3 \ \longrightarrow \ \lim_{x\to -2}f(x)=3$

Aan de andere kant zijn op het punt x=4 de laterale grenzen verschillend, aangezien de functie van links naar f(x)=3 nadert, maar van rechts naar f(x)=2. De limiet van de functie op dit punt bestaat daarom niet.

$\displaystyle\lim_{x\to 4^-}f(x)=3 \neq \lim_{x\to 4^+}f(x)=2 \ \longrightarrow \ \cancel{\exists} \ \lim_{x\to 4}f(x)$

Berekening van laterale limieten

Gegeven de definitie van laterale limieten, zullen we zien hoe ze numeriek worden berekend door het volgende voorbeeld op te lossen:

$\displaystyle\lim_{x\to 2}\frac{3}{x-2}$

Als we de limiet zoals gewoonlijk berekenen, verkrijgen we de onbepaaldheid van een reëel getal gedeeld door 0:

$\displaystyle\lim_{x\to 2}\frac{3}{x-2}=\frac{3}{2-2}=\frac{3}{0}=\infty$

Bij het berekenen van de laterale grenzen krijgen we echter geen onbepaaldheid.

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\ \color{red}\bm{?}\color{black} \qquad \lim_{x\to 2^+}\frac{3}{x-2}=\ \color{red}\bm{?}$

Om de laterale limiet van de functie vanaf links op x=2 te berekenen, moet je een getal nemen dat kleiner is dan x=2 maar er heel dichtbij ligt, bijvoorbeeld x=1,999.

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{\color{red}\bm{1,999}\color{black}-2}$

In dit geval is de noemer een negatief getal met een zeer kleine waarde, maar niet eens nul, en wordt deze meestal weergegeven door een nul en een minteken ervoor:

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{1,999-2}=\frac{3}{\color{red}\bm{-0}\color{black}}$

Daarom is het resultaat van de laterale limiet minus oneindig, omdat elk getal gedeeld door 0 oneindig geeft, en positief gedeeld door negatief negatief geeft:

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{1,999-2}=\frac{3}{-0}=\color{red}\bm{-\infty}\color{black}$

We kunnen verifiëren dat de functie min oneindig benadert door afbeeldingen van de functie te berekenen met waarden dichter bij x=2 vanaf de linkerkant.

$\begin{array}{c}\begin{array}{l}f(1,9)=\cfrac{3}{1,9-2}=-30\\[2ex]f(1,99)=\cfrac{3}{1,99-2}=-300\\[2ex]f(1,999)=\cfrac{3}{1,999-2}=-3000\\[2ex]f(1,9999)=\cfrac{3}{1,9999-2}=-30000\\[2ex]f(1,99999)=\cfrac{3}{1,99999-2}=-300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^-)=-\infty\end{array}$

Op dezelfde manier kunnen we, om de limiet van de functie op het punt x=2 aan de rechterkant te vinden, dezelfde redenering toepassen: we nemen een waarde groter dan 2 maar zeer dichtbij, zoals 2001.

$\displaystyle\lim_{x\to 2^+}\frac{3}{x-2}=\frac{3}{2,001-2}=\frac{3}{+0}=+\infty$

Op dezelfde manier kunnen we verifiëren dat de functie naar oneindig neigt door afbeeldingen van de functie te berekenen met waarden steeds dichter bij x=2 vanaf de rechterkant.

$\begin{array}{c}\begin{array}{l}f(2,1)=\cfrac{3}{2,1-2}=30\\[2ex]f(2,01)=\cfrac{3}{2,01-2}=300\\[2ex]f(2,001)=\cfrac{3}{2,001-2}=3000\\[2ex]f(2,0001)=\cfrac{3}{2,0001-2}=30000\\[2ex]f(2,00001)=\cfrac{3}{2,00001-2}=300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^+)=+\infty\end{array}$

In de volgende grafiek ziet u de geanalyseerde functie weergegeven. Zoals je kunt zien is de laterale limiet van de functie op het punt x=2 aan de linkerkant minus oneindig, en de laterale limiet van de functie op het punt x=2 aan de rechterkant is plus oneindig.

Problemen met de laterale grenzen opgelost

Oefening 1

Zoek de laterale grenzen van de volgende stuksgewijs gedefinieerde functie op de punten waar de definitie verandert (x=-2 en x=4).

zie oplossing

De laterale grenzen vallen niet samen op het punt x=-2, aan de linkerkant neigt de functie naar f(x)=5 en aan de andere kant is de functie aan de rechterkant constant en 3 waard.

$\displaystyle\lim_{x\to -2^-}f(x)=5$

$\displaystyle\lim_{x\to -2^+}f(x)=3$

De zijgrenzen zijn ook verschillend naarmate x 4 nadert. De stuksgewijze functie benadert 3 van links, maar benadert -2 van rechts.

$\displaystyle\lim_{x\to 4^-}f(x)=3$

$\displaystyle\lim_{x\to 4^+}f(x)=-2$

Oefening 2

Bepaal of de limiet bestaat als x 3 van de volgende stuksgewijze functie nadert, en zo ja, wat is de waarde ervan.

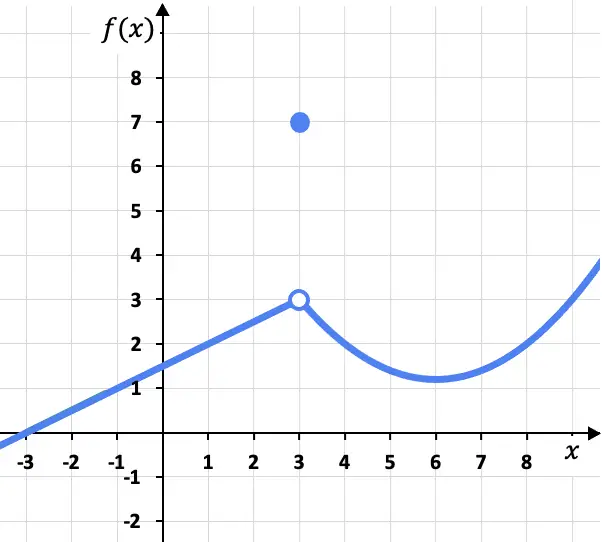
Laterale grenzen van een stuksgewijze functie

zie oplossing

In dit probleem zijn de laterale grenzen op het punt x=3 van links en van rechts identiek, aangezien de functie naar dezelfde waarde (f(x)=3) neigt, ongeacht of deze van links of van rechts wordt benaderd . zijn rechterkant:

$\displaystyle\lim_{x\to 3^-}f(x)=3$

$\displaystyle\lim_{x\to 3^+}f(x)=3$

Daarom is, volgens de wiskundige definitie van de limiet, de limiet van de functie wanneer x naar 3 neigt gelijk aan 3, omdat de twee laterale limieten op hetzelfde punt samenvallen op deze waarde:

$\displaystyle\lim_{x\to 3^-}f(x)=\lim_{x\to 3^+}f(x)=3 \ \longrightarrow \ \lim_{x\to 3}f(x)=3$

Hoewel de limiet van de functie op x=3 3 is, moet er rekening mee worden gehouden dat de functie op dit punt niet 3 is, maar dat f(3)=7. Zoals we later zullen zien, betekent dit dat de functie niet continu is op x=3, maar eerder een vermijdbare discontinuïteit heeft.

Oefening 3

Bereken de laterale grenzen van de volgende rationale functie op het punt x=4.

$f(x)=\cfrac{-2x+3}{x-4}$

zie oplossing

Om de limiet te berekenen wanneer x van links naar 4 neigt, nemen we een waarde kleiner dan 4 maar heel dichtbij, bijvoorbeeld 3.999:

$\displaystyle\lim_{x\to 4^-}\frac{-2x+3}{x-4}=\frac{-2\cdot 3,999+3}{3,999-4}=\frac{-4,998}{-0}=+\infty$

Dus de laterale limiet als x van links naar 4 nadert, is plus oneindig.

En om de limiet op te lossen wanneer x van rechts naar 4 neigt, evalueren we de functie op een waarde groter dan 4 maar heel dichtbij, bijvoorbeeld 4.001:

$\displaystyle\lim_{x\to 4^+}\frac{-2x+3}{x-4}=\frac{-2\cdot 4,001+3}{4,001-4}=\frac{-5,002}{+0}=-\infty$

Dus de laterale limiet als x van rechts naar 4 nadert, is minus oneindig.

Oefening 4

Zoek de limiet, als deze bestaat, van de volgende stuksgewijs gedefinieerde functie op het punt x=2:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2-3 & \text{si} & x \leq 2 \\[2ex]\displaystyle \frac{-3x+5}{x-3} & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”75″ width=”235″ style=”vertical-align: 0px;”></p> </p> <div class=$

zie oplossing

In dit geval vraagt de probleemstelling ons om de limiet te vinden waar de stuksgewijze functie van expressie verandert, dus moeten we de limiet aan de linkerkant vinden met behulp van de eerste uitdrukking en de limiet aan de rechterkant met behulp van de tweede uitdrukking.

$\displaystyle\lim_{x\to 2^+}f(x)=\lim_{x\to 2^+}\frac{-3x+5}{x-3}=\frac{-3\cdot 2+5}{2-3}=\frac{-1}{-1}=1$

De limiet van de functie op x=2 aan de linkerkant valt samen met de limiet van de functie aan de rechterkant, dus de limiet van de functie bestaat en is gelijk aan 1:

$\displaystyle\lim_{x\to 2^-}f(x)=\lim_{x\to 2^+}f(x)=1 \ \longrightarrow \ \lim_{x\to 2}f(x)=1$

Wat zijn de laterale grenzen?

Laterale grenzen links en rechts

gelijke laterale grenzen

Berekening van laterale limieten

Problemen met de laterale grenzen opgelost

Oefening 1

Oefening 2

Oefening 3

Oefening 4

Laat een reactie achter Reactie annuleren