Polynomiale functie

Hier vindt u wat polynoomfuncties zijn en wat alle soorten polynoomfuncties zijn. Daarnaast leggen we ook de eigenschappen van polynomiale functies uit.

Wat is een polynomiale functie?

Een polynoomfunctie is een functie waarvan de algebraïsche uitdrukking een polynoom is , dat wil zeggen dat een polynoomfunctie wordt gedefinieerd door het optellen of aftrekken van een eindig aantal termen van verschillende graad.

Daarom wordt een polynoomfunctie wiskundig beschreven door de volgende uitdrukking:

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

Aan de andere kant kunnen polynoomfuncties ook worden gedefinieerd met behulp van de volgende formule:

$\displaystyle f(x)=\sum_{k=0}^{n}a_k\cdot x^k$

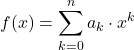
waar de voorwaarden

$a_k$

$x^k$

zijn respectievelijk de coëfficiënt en de variabele van elke monomiaal die de polynoomfunctie vormt.

De voorwaarde

$a_nx^n$

, de hoofdterm genoemd, geeft de graad van de polynoomfunctie aan, aangezien dit de hoogste graad monomiaal van de functie is. Met andere woorden: de exponent met de grootste waarde is degene die de graad van de polynoomfunctie aangeeft.

Hoewel we hieronder meer kenmerken van polynomiale functies zullen zien, bestaat het domein van elke polynoomfunctie uitsluitend uit reële getallen.

Soorten polynomiale functies

Gegeven de definitie van polynoomfunctie, zullen we nu zien welke soorten polynoomfuncties er bestaan.

constante functie

De constante functie is een polynomiale functie van graad 0, dus het is een type functie dat altijd hetzelfde beeld aanneemt voor elke waarde van de onafhankelijke variabele (x).

De algemene uitdrukking voor de constante functie is als volgt:

$f(x)=k$

De volgende drie functies zijn bijvoorbeeld constanten of polynomiale functies van graad nul:

$f(x)=5 \qquad f(x)=2 \qquad f(x)=-3$

De grafische weergave van een constante functie is een horizontale lijn (parallel aan de x-as) met een waarde gelijk aan de constante.

Meer functies over dit type functie vindt u via de volgende link:

➤ Zie: kenmerken van de constante functie

Lineaire functie

Een lineaire functie , ook wel een affiene functie genoemd, is een polynoomfunctie van de eerste graad. Een polynomiale functie van dit type kan dus alleen bestaan uit een lineaire term en een onafhankelijke term:

$f(x)=mx+n$

Goud

$m$

is de helling van de lijn en

$n$

is het y-snijpunt, dat wil zeggen waar de functie de Y-as kruist.

Voorbeelden van lineaire functies of polynomiale functies van de eerste graad:

$f(x)=4x+3\qquad f(x)=-5x$

Sommigen onderscheiden de lineaire functie van de affiene functie, afhankelijk van of de functie als term heeft

$n$

of niet, zijnde de affiene functie met het snijpunt en de lineaire functie zonder.

De grafische weergave van lineaire functies bestaat altijd uit lijnen waarvan de hellingsgraad afhangt van de waarde van de helling van de functie.

Hieronder ziet u grafisch de polynoomfunctie van de eerste graad

$f(x)=2x-1.$

Als u echter een lineaire functie wilt tekenen, moet u duidelijk zijn over verschillende concepten. In de volgende link vindt u stapsgewijze uitleg over hoe u een polynoomfunctie van dit type kunt tekenen:

➤ Zie: Grafische weergave van een lineaire functie

Kwadratische functie

Een kwadratische functie is een polynoomfunctie van graad 2, dat wil zeggen een functie waarvan de term van hogere graad van tweede graad is.

Daarom is de formule voor een kwadratische functie:

$f(x)=ax^2+bx+c$

Goud

$ax^2$

is de kwadratische term,

$bx$

de lineaire term en

$c$

de onafhankelijke term van de polynoomfunctie.

Voorbeelden van kwadratische functies of kwadratische polynoomfuncties:

$f(x)=5x^2+2x-1\qquad f(x)=-2x^2+x+7$

De grafiek van een kwadratische functie is altijd een parabool en de vorm ervan hangt af van het teken van de leidende coëfficiënt.

$a:$

Als de coëfficiënt
$a$

positief is, is de kwadratische functie convex (vorm als

$\bm{\cup}$

).
In plaats daarvan, als de coëfficiënt
$a$

negatief is, is de kwadratische functie concaaf (in de vorm van

$\bm{\cap}$

).

Met het teken van de hoofdcoëfficiënt van de kwadratische polynoomfunctie kunnen we dus de vorm kennen die de grafiek zal aannemen, maar om de exacte grafische weergave ervan te maken, moet een specifieke procedure worden gevolgd. U kunt deze procedure bekijken via de volgende link:

➤ Zie: Grafische weergave van een kwadratische functie

kubieke functie

Een kubieke functie is een polynomiale functie van de derde graad. Daarom wordt dit type polynoomfuncties algebraïsch als volgt uitgedrukt:

$f(x)=ax^3+bx^2+cx+d$

Voorbeelden van kubieke functies of polynomiale functies van de derde graad:

$f(x)=x^3+4x^2+5x-1$

$f(x)=2x^3-3x^2+9$

Grafische weergaven van kubieke functies komen overeen met kubieke curven. Om dit soort functies in een grafiek weer te geven, moet echter een ingewikkelde procedure worden gevolgd (inclusief afgeleiden). Je kunt hier zien hoe het moet:

➤ Zie:Een functie weergeven

Zoals u kunt zien, zijn de soorten polynoomfuncties feitelijk oneindig, aangezien een polynoom oneindige termen kan hebben. Een vierdegraadsfunctie lijkt dus op een derdegraadsfunctie, maar dan met toevoeging van een kwadratische term. Het belangrijkste is dat u begrijpt dat het type polynomiale functie wordt bepaald door de mate van de functie.

Eigenschappen van polynomiale functies

Polynomiale functies hebben de volgende kenmerken:

Het domein van elke polynomiale functie is de verzameling reële getallen.

$\text{Dom } f=\mathbbf{R}$

Alle polynomiale functies zijn continu.

Polynomiale functies met een graad groter dan 1 hebben geen asymptoten.

Ongeacht het type polynoomfunctie, het enige snijpunt met de ordinaat-as (Y-as) bevindt zich op de hoogte van zijn onafhankelijke term, dat wil zeggen op het volgende punt:

$(0,a_0)$

Aan de andere kant onderschept een polynoomfunctie de abscis-as (X-as), maximaal zo vaak als de graad van de functie.

Als een polynoomfunctie alleen termen van even graad heeft, impliceert dit dat deze symmetrisch is rond de OY-as. Aan de andere kant, als een polynoomfunctie alleen termen van oneven graad heeft, betekent dit dat de functie symmetrisch is ten opzichte van de oorsprong van de coördinaten.

Het aantal relatieve extrema (maximum of minimum) van een polynoomfunctie is hoogstens de graad van het polynoom van de functie minus 1.

Het aantal buigpunten van een polynoomfunctie is maximaal gelijk aan de graad van het polynoom van de functie minus 2.

Bewerkingen kunnen worden uitgevoerd met polynomiale functies:
- De som van twee polynoomfuncties levert een andere polynoomfunctie op.
- Het product van twee polynoomfuncties geeft aanleiding tot een andere polynoomfunctie.
- Het vermenigvuldigen van een polynoomfunctie met een scalair (reëel getal) resulteert in een vergelijkbare polynoomfunctie, maar met een verkleinde of uitgebreide grafiek.
- De samenstelling van twee polynoomfuncties is gelijk aan een andere polynoomfunctie.