Symmetrie van een functie: symmetrische en asymmetrische functie

In dit artikel leggen we uit wat symmetrische functies zijn (even en oneven functies) en hoe je de symmetrie van een functie kunt bestuderen. Je zult ook de eigenschappen van dit soort functies kunnen zien en ten slotte kun je oefenen met stap voor stap opgeloste oefeningen van symmetrische functies.

Wat is een symmetrische functie?

Een symmetrische functie is een functie waarin een symmetrieas in zijn grafische weergave kan worden gevonden. Er zijn twee soorten symmetrische functies: even functies, symmetrisch rond de Y-as, en oneven functies, symmetrisch rond de oorsprong van de coördinaten.

Bedenk dat een symmetrieas een denkbeeldige lijn is die iets in twee delen verdeelt, zodat de tegenovergestelde punten op gelijke afstand van elkaar liggen.

zelfs functies

Zelfs functies zijn functies die symmetrisch zijn rond de y-as, dat wil zeggen dat de Y-as een symmetrieas van de functie is.

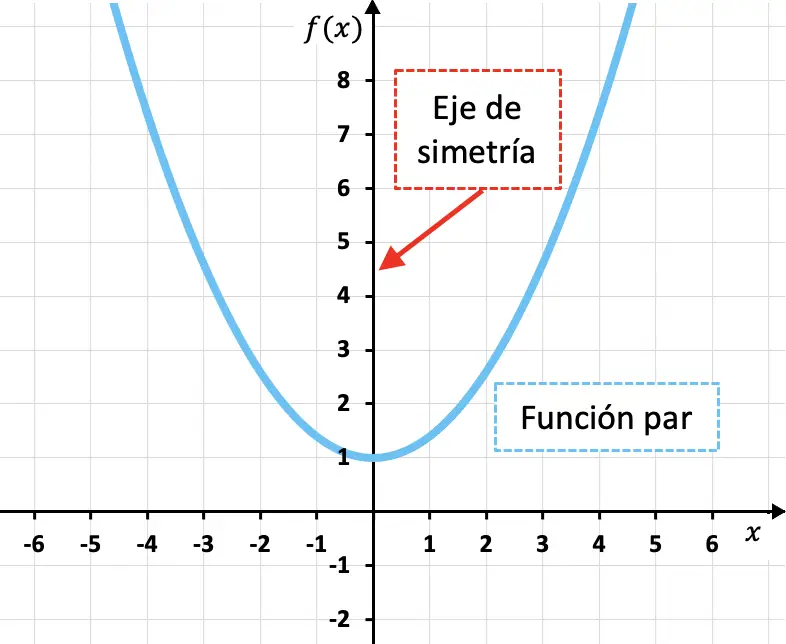
Zoals je kunt zien in de kwadratische functie hierboven, is het beeld van een even functie voor elke waarde van de onafhankelijke variabele (x) equivalent aan het beeld van de functie voor de tegenovergestelde waarde (-x). Met andere woorden, wiskundig gezien is een functie zelfs als deze aan de volgende voorwaarde voldoet:

Even functies zijn een soort symmetrische functies. Laten we nu eens kijken hoe oneven functies eruit zien.

vreemde functies

Oneven functies zijn functies die symmetrisch zijn ten opzichte van de oorsprong van de coördinaten, dat wil zeggen ten opzichte van het punt (0,0).

Hieronder ziet u een vreemde functie in grafiekvorm:

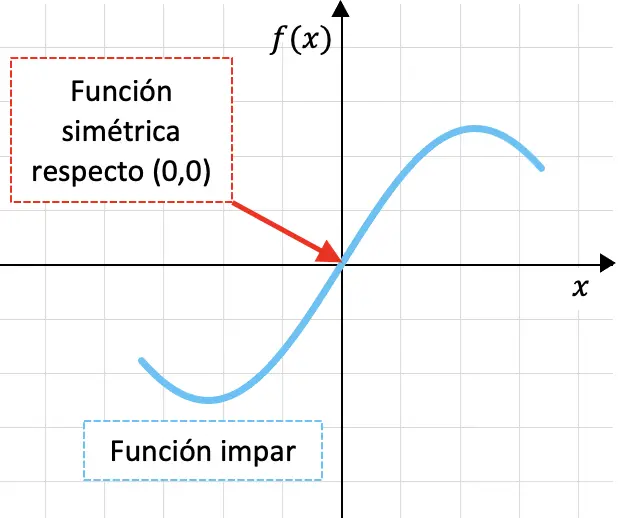
Het feit dat een functie symmetrisch is ten opzichte van de coördinaatoorsprong betekent dat als we de grafiek van de functie eerst door de OY-as en vervolgens door de OX-as vouwen, de grafiek van de functie zou overlappen.

Algebraïsch gezien is een functie oneven als aan de volgende relatie tussen de afbeeldingen is voldaan:

Het kennen van de symmetrie van een functie is erg handig om deze weer te geven, omdat we, als we slechts de ene helft van de grafiek kennen, snel het andere deel kunnen tekenen.

Hoe de symmetrie van een functie te vinden

Om de symmetrie van een functie te bestuderen, moeten we het beeld ervan berekenen

, dat wil zeggen dat het noodzakelijk is om te berekenen

Dus, afhankelijk van het resultaat van de afbeelding, zal de symmetrie van de functie zijn:

1. als deze gevuld is

   

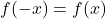
   , de functie is even en daarom symmetrisch ten opzichte van de Y-as.

2. als deze gevuld is

   

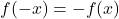
   , de functie is oneven en daarom symmetrisch ten opzichte van de oorsprong van de coördinaten.

3. Als aan geen van de bovenstaande voorwaarden is voldaan, is er sprake van een asymmetrische functie (deze heeft geen symmetrieas).

Laten we bijvoorbeeld de symmetrie van de volgende kubieke functie analyseren:

Om de symmetrie van de functie te bestuderen, berekenen we

De resulterende algebraïsche uitdrukking is equivalent aan de oorspronkelijke functie-uitdrukking, maar is van teken veranderd, of met andere woorden, er is voldaan aan de volgende gelijkheid:

De functie is dus oneven en dus symmetrisch ten opzichte van de oorsprong van de coördinaten (0,0).

Eigenschappen van symmetrische functies

Symmetrische functies hebben de volgende kenmerken:

• De som van twee even/oneven functies is gelijk aan een andere even/oneven functie.
• Het product van twee even functies of twee oneven functies geeft een even functie.
• De afgeleide van een even/oneven functie is een even/oneven functie.
• De samenstelling tussen twee even/oneven functies is gelijkwaardig aan een even/oneven functie.
• De enige functie die zowel even als oneven is, dat wil zeggen symmetrisch ten opzichte van de OY-as en ten opzichte van de oorsprong, is de functie

  

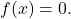
Opgeloste problemen van de symmetrie van een functie

Oefening 1

Zoek de symmetrie van de volgende functie:

Om de symmetrie van de functie te berekenen, moeten we evalueren

Elke macht van een negatief getal verhoogd tot een exponent levert een positief getal op, dus in dit geval is de volgende vergelijking waar:

De functie is daarom even en daarom symmetrisch rond de y-as (Y-as).

Oefening 2

Bestudeer de symmetrie van de volgende rationale functie:

Om de symmetrie van de functie te bepalen, doen we dat

In dit probleem wordt aan geen enkele symmetrievoorwaarde voldaan, omdat het beeld van

is niet gelijk aan

noch aan

De functie heeft dus geen symmetrieas, maar is eerder een asymmetrische functie.

Oefening 3

Bereken de symmetrie van de volgende functie:

Om de symmetrie van de functie te analyseren, moeten we berekenen

In dit geval is de resulterende uitdrukking gelijk aan de oorspronkelijke uitdrukking, maar met een verandering van teken. Er is dus voldaan aan de volgende vergelijking:

De functie is dus oneven en dus symmetrisch ten opzichte van de oorsprong van de coördinaten (0,0).