Op deze pagina vind je alles over de hyperbolische tangens: wat is de formule, de grafische weergave, al zijn kenmerken,…
Hyperbolische raaklijnformule
De hyperbolische tangensfunctie is een van de belangrijkste hyperbolische functies en wordt weergegeven door het symbool tanh(x) . Wiskundig gezien is de hyperbolische tangens gelijk aan de hyperbolische sinus gedeeld door de hyperbolische cosinus.
![]()
Uit de hyperbolische sinusformule en de hyperbolische cosinusformule kunnen we tot de volgende uitdrukking komen:
![]()
Daarom is de hyperbolische tangensfunctie gerelateerd aan de exponentiële functie. In de volgende link kunt u alle kenmerken van dit soort functies bekijken:
➤ Zie: kenmerken van exponentiële functies
Grafische weergave van de hyperbolische tangens
Uit de formule kunnen we de hyperbolische tangensfunctie grafisch weergeven:
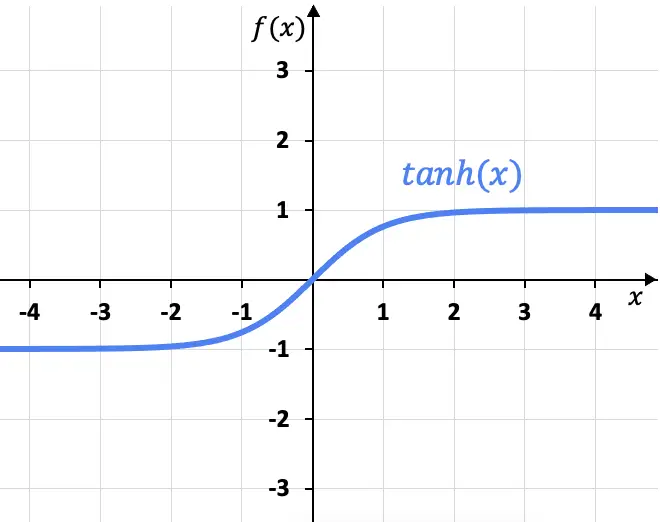
Zoals je in de grafiek kunt zien, heeft de hyperbolische tangensfunctie twee horizontale asymptoten op x=+1 en x=-1, aangezien de limiet van de functie als x plus oneindig nadert x=+1 oplevert, en de limiet tot minus oneindig geeft x=-1.
Aan de andere kant heeft de grafiek van de hyperbolische raaklijn niets te maken met de grafiek van de raaklijn (trigonometrische functie), die een periodieke functie is. U kunt de grafische weergave van de raaklijn en hoe deze verschilt van de hyperbolische raaklijn zien in de volgende link:
➤ Zie: grafische weergave van de raaklijnfunctie
Kenmerken van de hyperbolische tangens
De hyperbolische tangensfunctie heeft de volgende eigenschappen:
- Het domein van de hyperbolische tangensfunctie bestaat uit alle reële getallen.
![]()
- Daarentegen is het pad of bereik van de hyperbolische tangensfunctie beperkt tot waarden tussen -1 en +1 (niet inclusief).
![]()
- De hyperbolische tangens is een continue, bijectieve en oneven functie (symmetrisch ten opzichte van de oorsprong van de coördinaten).
![]()
- De functie snijdt de X-as en de Y-as op de coördinaatoorsprong.
![]()
- De limieten voor plus/minus oneindig van de hyperbolische tangensfunctie geven +1/-1. Daarom heeft de functie een horizontale asymptoot op x=+1 en een andere horizontale asymptoot op x=-1.
![]()
![]()
- De hyperbolische tangens neemt over het gehele domein strikt toe en heeft daarom geen relatieve extrema (noch maximum noch minimum).
- De functie verandert echter van convex naar concaaf op het punt x = 0, dus x = 0 is een buigpunt van de functie.
- Het omgekeerde van de hyperbolische tangensfunctie wordt het hyperbolische tangens- (of hyperbolische boogtangens-) argument genoemd en de formule is als volgt:
![]()
- De afgeleide van de hyperbolische tangensfunctie is 1 gedeeld door het kwadraat van de hyperbolische cosinus:
![]()
- De integraal van de hyperbolische tangensfunctie is de natuurlijke logaritme van de hyperbolische cosinus:
![]()
- De hyperbolische tangens van de som van twee verschillende getallen kan worden berekend door de volgende vergelijking toe te passen:
![]()
- De Taylor-polynoom of de hyperbolische raaklijnreeks heeft de convergentiestraal
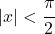
en komt overeen met de volgende uitdrukking:
![]()
Goud
![]()
is het Bernoulligetal .