In dit artikel leggen we uit wat de periodiciteit van een functie is. Daarnaast ziet u verschillende voorbeelden van periodieke functies. Ten slotte zullen we de periode van trigonometrische functies analyseren, aangezien dit een van de belangrijkste kenmerken ervan is.
Wat is de periodiciteit van een functie?
De periodiciteit van een functie is een kenmerk van functies die hun waarden cyclisch herhalen, dat wil zeggen dat een functie periodiek is als de grafiek zich op elk bepaald interval herhaalt. Dit interval wordt een periode genoemd.
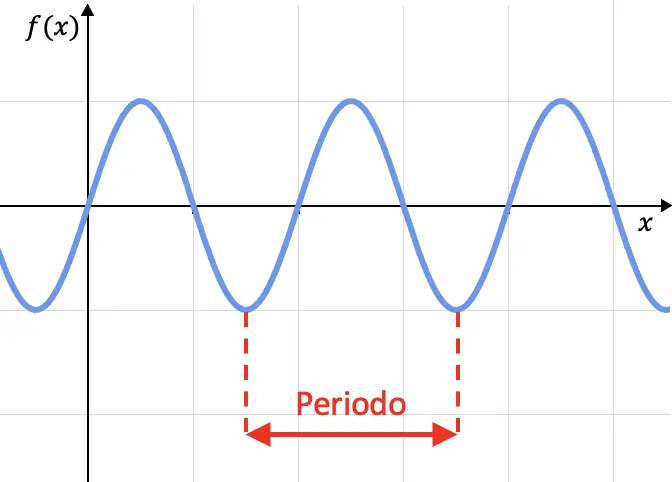
Wiskundig gezien wordt een functie als periodiek gedefinieerd als deze alleen wordt vervuld
![]()
voor elke waarde van de onafhankelijke variabele x.
![]()
Waarbij T de periode is van de periodieke functie ik geheel getal.
Voorbeelden van functieperiodiciteiten
Zodra we het concept van periodiciteit van een functie hebben gezien, zullen we verschillende voorbeelden zien van hoe de periodiciteit van een functie kan worden berekend.
voorbeeld 1
Bepaal of de volgende functie periodiek is:
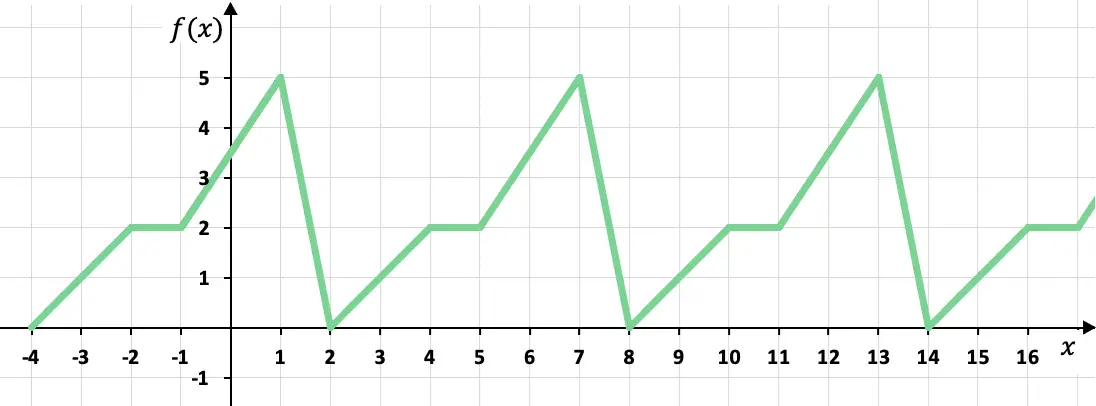
Deze stuksgewijs gedefinieerde functie is een periodieke functie, aangezien de waarden van de grafiek cyclisch worden herhaald. Preciezer gezegd: de functie neemt elke zes x dezelfde waarde aan, daarom is de periode van de functie gelijk aan 6.
![]()
Voorbeeld 2
Zoek de periodiciteit van de volgende functie:
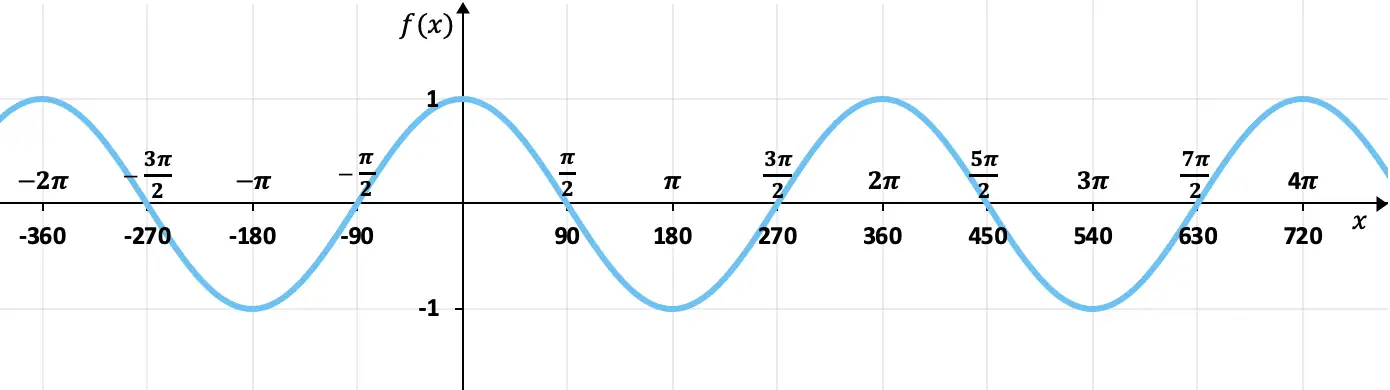
Deze functie komt overeen met de grafische weergave van een trigonometrische functie, meer bepaald de cosinusfunctie.
Zoals we in de grafiek kunnen zien, herhaalt de functie zijn waarden periodiek, dus het is een periodieke functie. Bovendien is er tussen de piek en de piek van de golf een ruimte van 2π (of 360º), dus dit is de periode van de functie.
![]()
Periodiciteit van trigonometrische functies
Periodiciteit en trigonometrische functies zijn nauw met elkaar verbonden. Een van de belangrijkste kenmerken van dit soort functies is dat de meeste trigonometrische functies periodiek zijn.
Vervolgens bestuderen we de periodiciteit van de 3 belangrijkste trigonometrische functies: sinus, cosinus en tangens.
Sinusfunctieperiode
De uitdrukking voor de sinusfunctie is als volgt:
![]()
In dit geval is het niet nodig om de functie in een grafiek weer te geven om de periode ervan te vinden, maar deze kan eenvoudig worden berekend door de volgende formule toe te passen:
![]()
Bovendien heeft de sinusfunctie de bijzonderheid dat als we de periode veranderen, we ook de vorm van de grafiek veranderen. Via de volgende link kunt u zien hoe de periodewaarde de grafische weergave beïnvloedt:
➤ Zie: Grafiek van de sinusfunctie
Periode van de cosinusfunctie
De algebraïsche uitdrukking voor de cosinusfunctie is als volgt:
![]()
Net als bij sinus kan de periode van de cosinusfunctie direct worden gevonden met behulp van de volgende formule:
![]()
De waarde van de cosinusperiode bepaalt volledig de grafiek, klik op de volgende link en ontdek waarom:
➤ Zie: Grafiek van de cosinusfunctie
Periode van de tangensfunctie
De tangensfunctie wordt wiskundig beschreven:
![]()
De periode van de raaklijnfunctie wordt berekend met dezelfde formule als die van de sinus en cosinus:
![]()
De tangensfunctiegrafiek verschilt echter van sinus en cosinus omdat deze ook asymptoten heeft die zich periodiek herhalen. U kunt deze en andere kenmerken van deze trigonometrische functie bekijken op de volgende link: