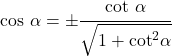Cosinusfunctie - Mathority

Op deze pagina vind je alles over de cosinusfunctie: wat is het, wat is de formule, hoe je het in een grafiek weergeeft, de kenmerken van de functie, amplitude, periode, etc. Bovendien kunt u verschillende voorbeelden van cosinusfuncties zien om het concept volledig te begrijpen. Het verklaart zelfs de cosinusstelling en de relaties die de cosinusfunctie heeft met andere trigonometrische verhoudingen.

cosinusfunctieformule

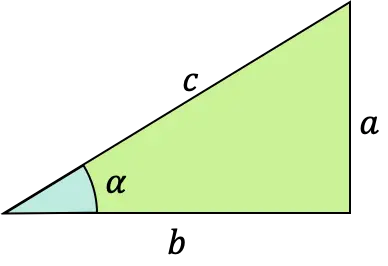
De cosinusfunctie van een hoek α is een trigonometrische functie waarvan de formule wordt gedefinieerd als de verhouding tussen het aangrenzende (of aangrenzende) been en de hypotenusa van een rechthoekige driehoek (driehoek met een rechte hoek).

wat is de formule voor de cosinusfunctie

Dit type wiskundige functie wordt ook wel een cosinus-, cosinus- of cosinusfunctie genoemd.

De cosinusfunctie is een van de drie bekendste trigonometrische verhoudingen, samen met de sinus en de tangens van een hoek.

Karakteristieke waarden van de cosinusfunctie

Sommige hoeken herhalen zich regelmatig en daarom is het handig om de waarde van de cosinusfunctie bij deze hoeken te kennen:

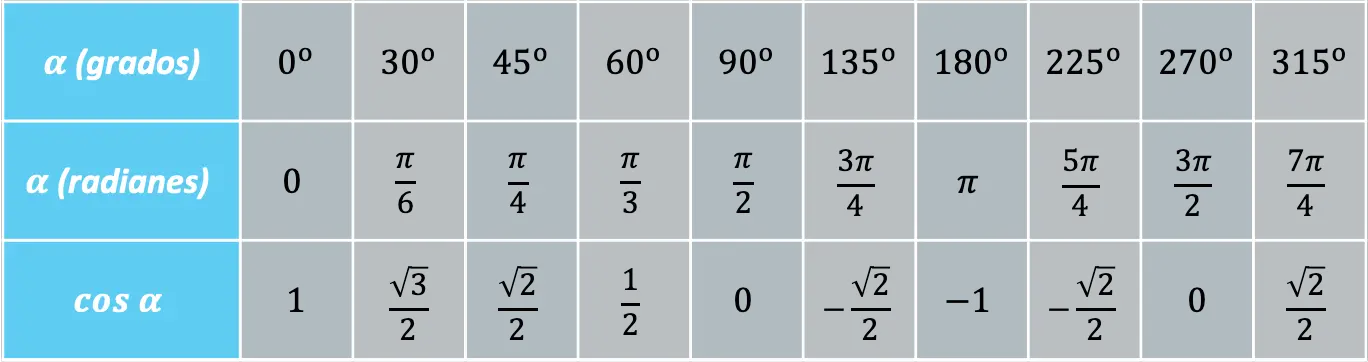
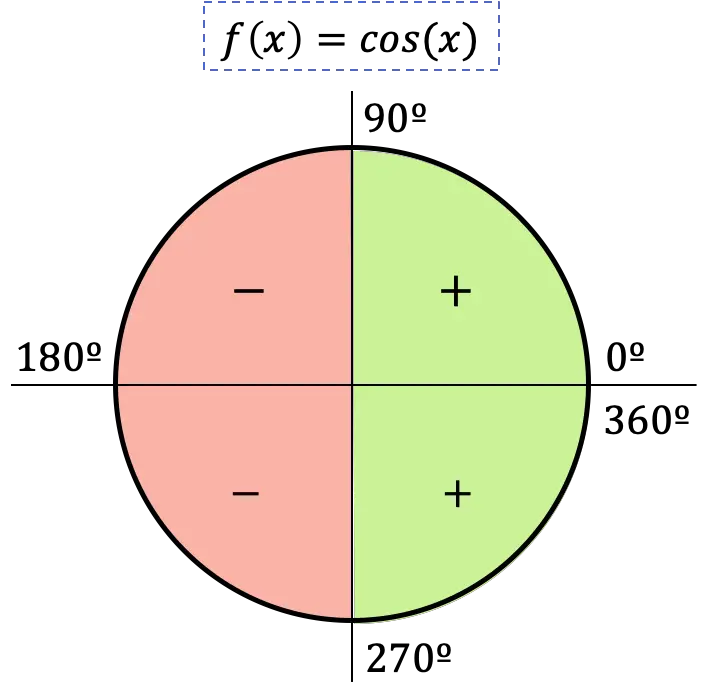
Het teken van de cosinusfunctie hangt dus af van het kwadrant waarin de hoek zich bevindt: als de hoek zich in het eerste of vierde kwadrant bevindt, zal de cosinus positief zijn, aan de andere kant als de hoek in het tweede of derde kwadrant valt. , zal de cosinus negatief zijn.

Grafische weergave van de cosinusfunctie

Met de waardentabel die we in de vorige sectie hebben gezien, kunnen we de cosinusfunctie in een grafiek weergeven. En door de cosinusfunctie in een grafiek weer te geven, verkrijgen we:

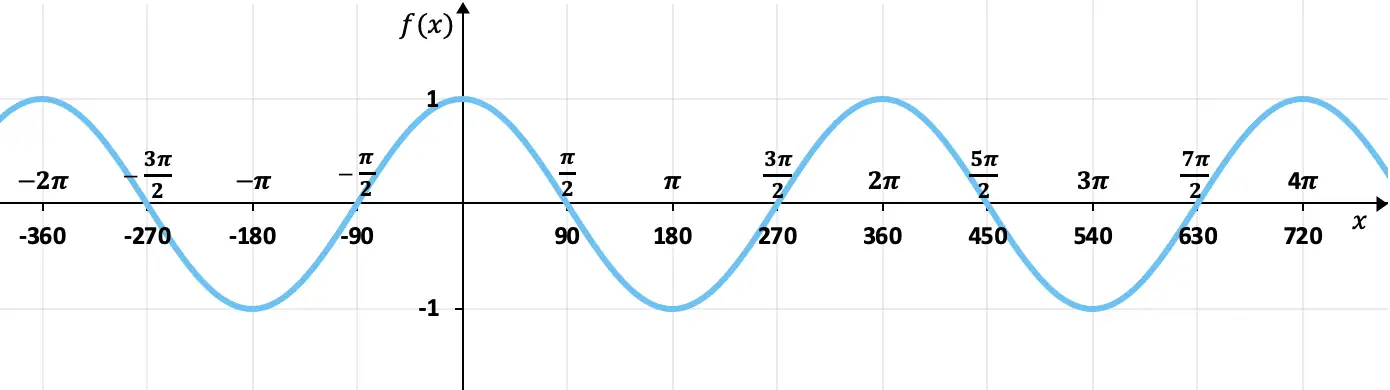
Zoals je in de grafiek kunt zien, liggen de waarden van de afbeeldingen van de cosinusfunctie altijd tussen +1 en -1, dat wil zeggen dat deze bovenaan wordt begrensd door +1 en onderaan door -1. Bovendien worden de waarden elke 360 graden herhaald (2π radialen), dus het is een periodieke functie waarvan de periode 360 graden is.

Aan de andere kant begrijpen we in deze grafiek perfect dat de cosinusfunctie even is, omdat de tegenovergestelde elementen hetzelfde beeld hebben, dat wil zeggen dat deze symmetrisch is ten opzichte van de computeras (Y-as). De cosinus van 90º is bijvoorbeeld 0 en die van -90º is 0.

Eigenschappen van de cosinusfunctie

De cosinusfunctie heeft de volgende kenmerken:

Het domein van de cosinusfunctie bestaat uitsluitend uit reële getallen, aangezien, zoals de grafiek laat zien, de functie bestaat voor elke waarde van de onafhankelijke variabele x.

$\text{Dom } f = \mathbb{R}$

Het pad of bereik van de cosinusfunctie is van negatief 1 tot positief 1 (beide inclusief).

$\text{Im } f= [-1,1]$

Het is een continue functie en een koppel met periodiciteit 2π.

$\displaystyle \text{cos }x = \text{cos}(-x)$

Dit type trigonometrische functie heeft één snijpunt met de OY-as op punt (0,1).

$(0,1)$

In plaats daarvan onderschept het periodiek de abscis (X-as) op oneven meerdere coördinaten van de gemiddelde pi.

$\displaystyle \left(\frac{\pi}{2}+k\pi ,0\right) \qquad k \in \mathbb{Z}$

Het maximum van de cosinusfunctie treedt op wanneer:

$x = 2\pi k \qquad k \in \mathbb{Z}$

En omgekeerd vindt het minimum van de cosinusfunctie plaats bij:

$x = \pi(2k +1 ) \qquad k \in \mathbb{Z}$

De afgeleide van de cosinusfunctie is de sinus waarvan het teken is veranderd:

$f(x)=\text{cos } x \ \longrightarrow \ f'(x)= -\text{sen } x$

Ten slotte is de integraal van de cosinusfunctie sinus:

$\displaystyle \int \text{cos } x \ dx= \text{sen } x + C$

Periode en amplitude van de cosinusfunctie

Zoals we in zijn grafiek zagen, is de cosinusfunctie een periodieke functie, dat wil zeggen dat de waarden ervan met een frequentie worden herhaald. Bovendien zijn de maximale en minimale waarden waartussen het oscilleert afhankelijk van de amplitude. Twee belangrijke kenmerken die de cosinusfunctie bepalen, zijn dus de periode en de amplitude:

$\displaystyle f(x)= A\text{cos}(wx)$

De periode van de cosinusfunctie is de afstand tussen twee punten waarop de grafiek wordt herhaald en wordt berekend met de volgende formule:

$\displaystyle \text{Periodo}=T=\cfrac{2\pi}{w}$

De grootte van de cosinusfunctie is equivalent aan de coëfficiënt vóór de cosinusterm.

$\displaystyle \text{Amplitud}=A$

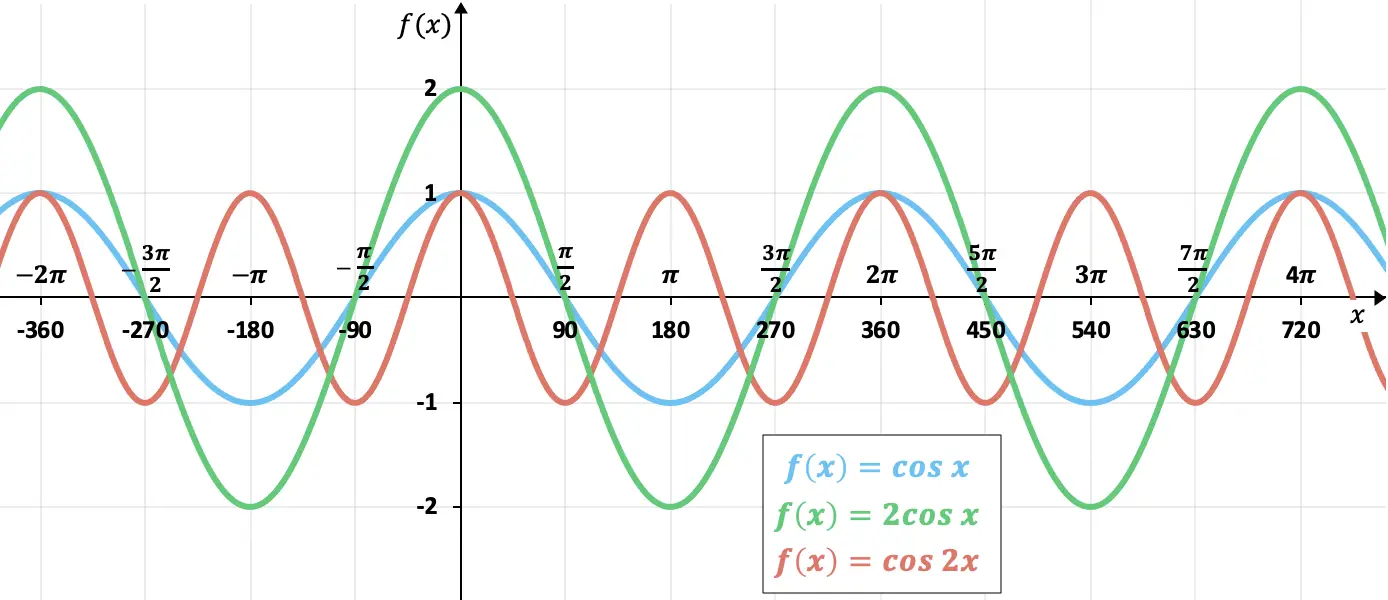
Hieronder ziet u een grafiek die de effecten laat zien van het veranderen van de periode of amplitude:

In de functie die groen wordt weergegeven, kunnen we zien dat door het verdubbelen van de amplitude de functie van +2 naar -2 gaat, in plaats van +1 naar -1. Aan de andere kant kun je in de rood weergegeven functie zien hoe deze twee keer zo snel gaat als de “canonieke” cosinusfunctie, aangezien de periode ervan is gehalveerd.

cosinus stelling

Hoewel de cosinusformule normaal gesproken wordt gebruikt in rechthoekige driehoeken, is er ook een stelling die op elk type driehoek kan worden toegepast: de cosinus of cosinusstelling.

De cosinusstelling relateert de zijden en hoeken van elke driehoek als volgt:

$a^2=b^2+c^2-2\cdot b \cdot c\cdot \text{cos }\alpha$

$b^2=a^2+c^2-2\cdot a \cdot c\cdot \text{cos }\beta$

$c^2=a^2+b^2-2\cdot a \cdot b\cdot \text{cos }\gamma$

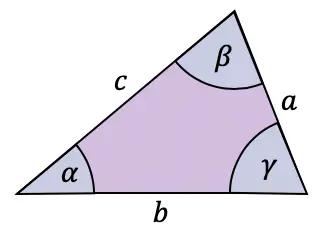
Relaties van de cosinusfunctie met andere trigonometrische verhoudingen

Dan heb je de cosinusrelaties met de belangrijkste goniometrische verhoudingen in de trigonometrie.

Relatie met de borst

De grafiek van de sinusfunctie is equivalent aan de cosinuscurve, maar verschoven
$\displaystyle \frac{\pi}{2}$

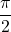
aan de rechterkant kunnen de twee functies daarom worden gekoppeld door de volgende uitdrukking:

$\displaystyle \text{cos }\alpha = \text{sen}\left(\alpha + \frac{\pi}{2} \right)$

Je kunt sinus en cosinus ook in verband brengen met de trigonometrische fundamentele identiteit:

$\displaystyle \text{sen}^2\alpha + \text{cos}^2\alpha=1$

relatie tot de raaklijn

Hoewel het ingewikkeld is om te bewijzen, kan de cosinus alleen worden uitgedrukt volgens de raaklijn:

$\displaystyle \text{cos }\alpha = \pm \cfrac{1}{\sqrt{1+\text{tg}^2\alpha \vphantom{\bigl( }}}$

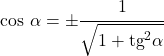
Relatie met de secans

De cosinus en secans zijn multiplicatieve inverses:

$\displaystyle \text{cos }\alpha = \cfrac{1}{\text{sec }\alpha}$

Relatie met de cosecant

De cosinus kan zo worden opgelost dat deze alleen van de cosecans afhangt:

$\displaystyle \text{cos }\alpha =\pm \cfrac{\sqrt{\text{csc}^2\alpha -1 } }{\text{csc }\alpha}$

Relatie met de cotangens

De cosinus en cotangens van een hoek zijn gerelateerd aan de volgende vergelijking:

$\displaystyle \text{cos }\alpha =\pm \cfrac{\text{cot }\alpha}{\sqrt{1+\text{cot}^2\alpha \vphantom{\bigl( }}}$

Cosinus-functie