Op deze pagina wordt uitgelegd wat inverse evenredigheidsfuncties zijn en hoe u deze kunt tekenen. Daarnaast vindt u alle kenmerken van dit type functie, hoe u het domein ervan kunt berekenen en ook verschillende voorbeelden en oefeningen die stap voor stap zijn opgelost om te oefenen.
Wat is een inverse evenredigheidsfunctie?
Een inverse evenredigheidsfunctie is een functie die twee omgekeerd evenredige grootheden met elkaar in verband brengt, dat wil zeggen dat de ene grootheid toeneemt wanneer de andere afneemt en omgekeerd. Over het algemeen worden inverse evenredigheidsfuncties gedefinieerd door de volgende formule:
![]()
Goud
![]()
is een constante die de evenredigheidsratio wordt genoemd.
Inverse evenredigheidsfuncties zijn dus altijd samengesteld uit breuken met een eerstegraadspolynoom in de noemer. Daarom zijn ze een soort rationele functie.
Voorbeelden van inverse evenredigheidsfuncties:
![]()
Over het algemeen
![]()
is over het algemeen de onafhankelijke variabele en
![]()
de afhankelijke variabele, of met andere woorden, de variabele
![]()
afhankelijk zijn van
![]()
Aan de andere kant kan de evenredigheidsratio (de tellerterm) positief of negatief zijn en het teken ervan markeert de toename of afname van de functie:
- Als de constante

negatief is, neemt de functie toe.
- In plaats daarvan, als de constante

positief is, is de functie afnemend.
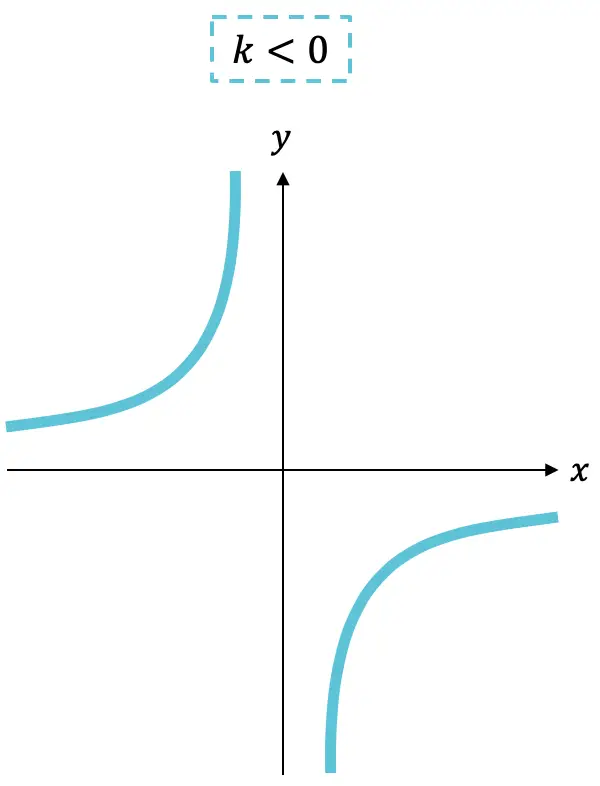
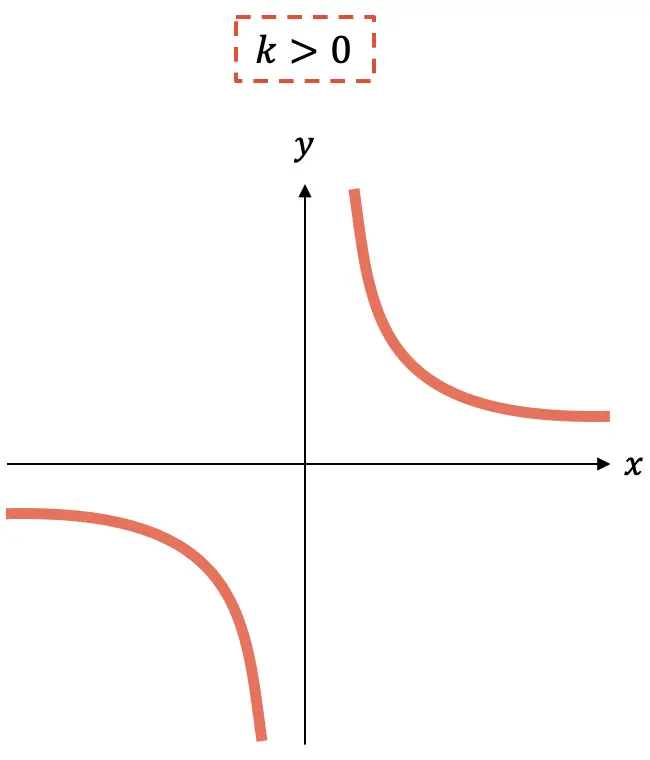
Zoals u kunt zien, bestaat de grafiek van een inverse evenredigheidsfunctie altijd uit twee hyperbolen die, afhankelijk van het teken van k , in het ene of het andere kwadrant zullen liggen.
Domein van een inverse evenredigheidsfunctie
Omdat het een soort rationale functie is, bestaat het domein van een inverse evenredigheidsfunctie uit alle reële getallen, behalve de getallen die uit de noemer verdwijnen . Omdat de noemer nooit nul kan zijn, omdat dat zou resulteren in oneindigheid.
Als voorbeeld zullen we het domein van de volgende inverse evenredigheidsfunctie bepalen:
![]()
Om te weten wanneer de noemer nul is, moeten we de uitdrukking ervan gelijkstellen aan 0 en de vergelijking oplossen:
![]()
![]()
Wanneer x dus de waarde 1 aanneemt, zal de noemer nul zijn en zullen we onbepaaldheid verkrijgen. Het domein van de functie bestaat dus uit alle reële getallen min
![]()
![]()
Hoe u een inverse evenredigheidsfunctie kunt tekenen
We zullen zien hoe we een inverse evenredigheidsfunctie kunnen tekenen aan de hand van een voorbeeld.
- We zullen de volgende functie in een grafiek weergeven:
![]()
Het eerste dat we moeten doen is het domein van de functie vinden. Omdat het een breuk is, kan de noemer nooit 0 zijn, omdat dat dan oneindig zou opleveren. Daarom zal het domein geheel x zijn, behalve wanneer de noemer wordt geannuleerd.
We stellen daarom de noemer gelijk aan 0 om te zien welke x niet tot het domein behoort:
![]()
![]()
Daarom bestaat het domein van de functie uit alle getallen behalve 2:
![]()
Zodra we weten welk nummer niet bij het domein hoort, maken we een tabel met waarden. Om functies van inverse evenredigheid weer te geven, is het nodig om 3 of 4 punten links en 3 of 4 punten rechts te berekenen van het getal dat niet tot domein (2) behoort:
![]()

Laten we nu de punten in een grafiek weergeven :
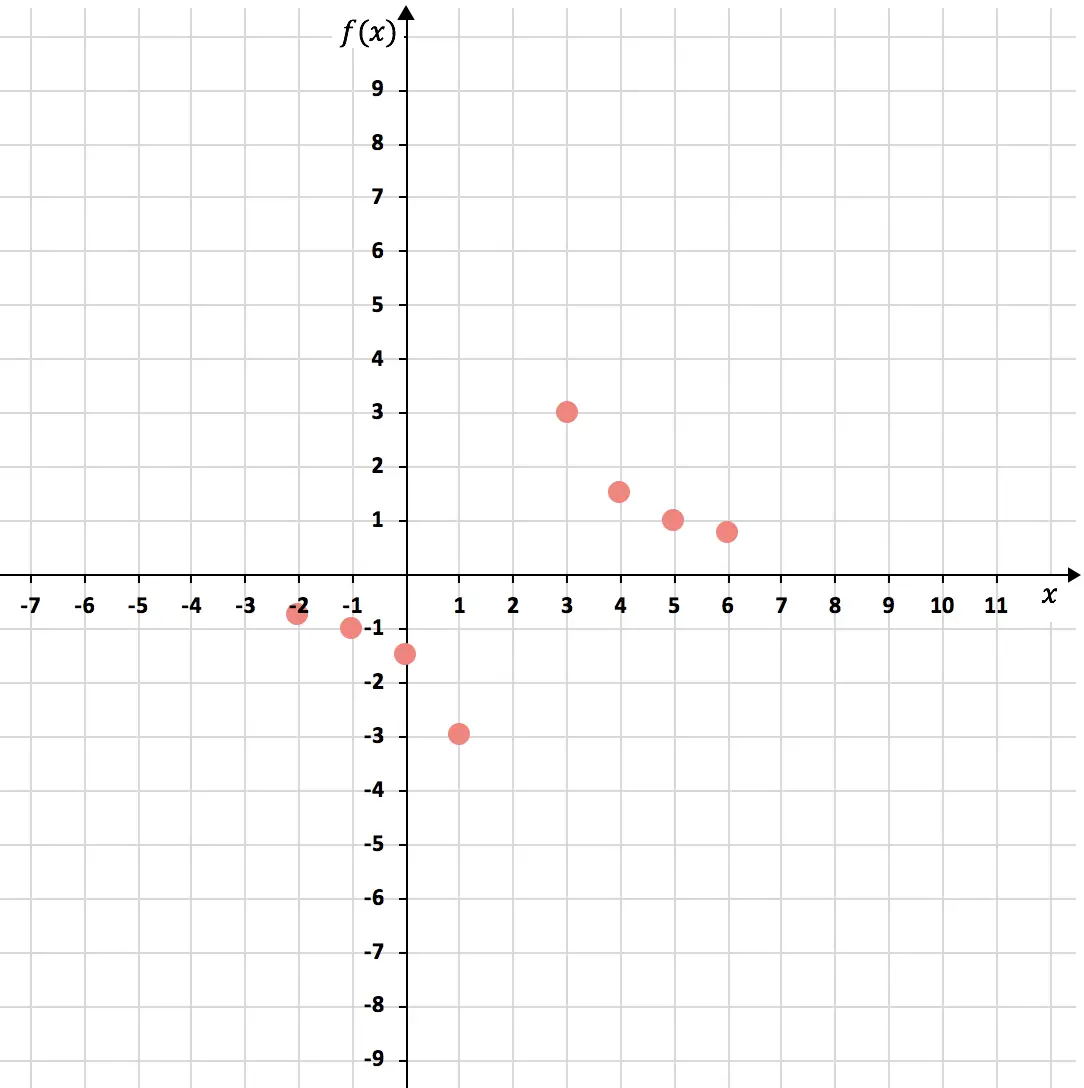
En tenslotte voegen we de punten samen, waardoor de twee hyperbolen van de inverse evenredigheidsfunctie ontstaan. Bovendien verlengen we de takken van de hyperbolen om aan te geven dat ze blijven groeien:

Merk op dat de functie bij benadering is
![]()
, zowel rechts als links. Het raakt echter nooit helemaal 2, het komt heel dichtbij maar raakt het nooit. DUS,
![]()
het is een verticale asymptoot . Het is omdat
![]()
behoort niet tot het domein van de functie en daarom bestaat de functie op dat moment niet.
En hetzelfde gebeurt met de horizontale X-as. De functie benadert
![]()
maar raak het nooit aan. Nog,
![]()
is een horizontale asymptoot .
Dit betekent dat alle inverse evenredigheidsfuncties discontinu zijn, omdat ze altijd een asymptoot hebben.
Op onze website kunt u meer te weten komen over asymptoten en functiegrenzen.
Problemen van inverse evenredigheidsfuncties opgelost
Oefening 1
Bereken het domein van de volgende inverse evenredigheidsfunctie:
![]()
Er bestaat geen inverse evenredigheidsfunctie als de noemer 0 is, omdat de functie dan ∞ zou opleveren. Daarom moeten we de noemer van de functie gelijk stellen aan 0 om te zien dat x de noemer annuleert en daarom niet tot het domein behoort.
![]()
![]()
![]()
![]()
Oefening 2
Grafiek van de volgende inverse evenredigheidsfunctie:
![]()
Het eerste dat u moet doen, is het domein van de functie berekenen:
![]()
![]()
Zodra we weten welk nummer niet bij het domein hoort, creëren we een array van waarden met de functie:

Ten slotte vertegenwoordigen we de verkregen punten in de grafiek en tekenen we de hyperbolen, waardoor we de inverse evenredigheidsfunctie vormen:
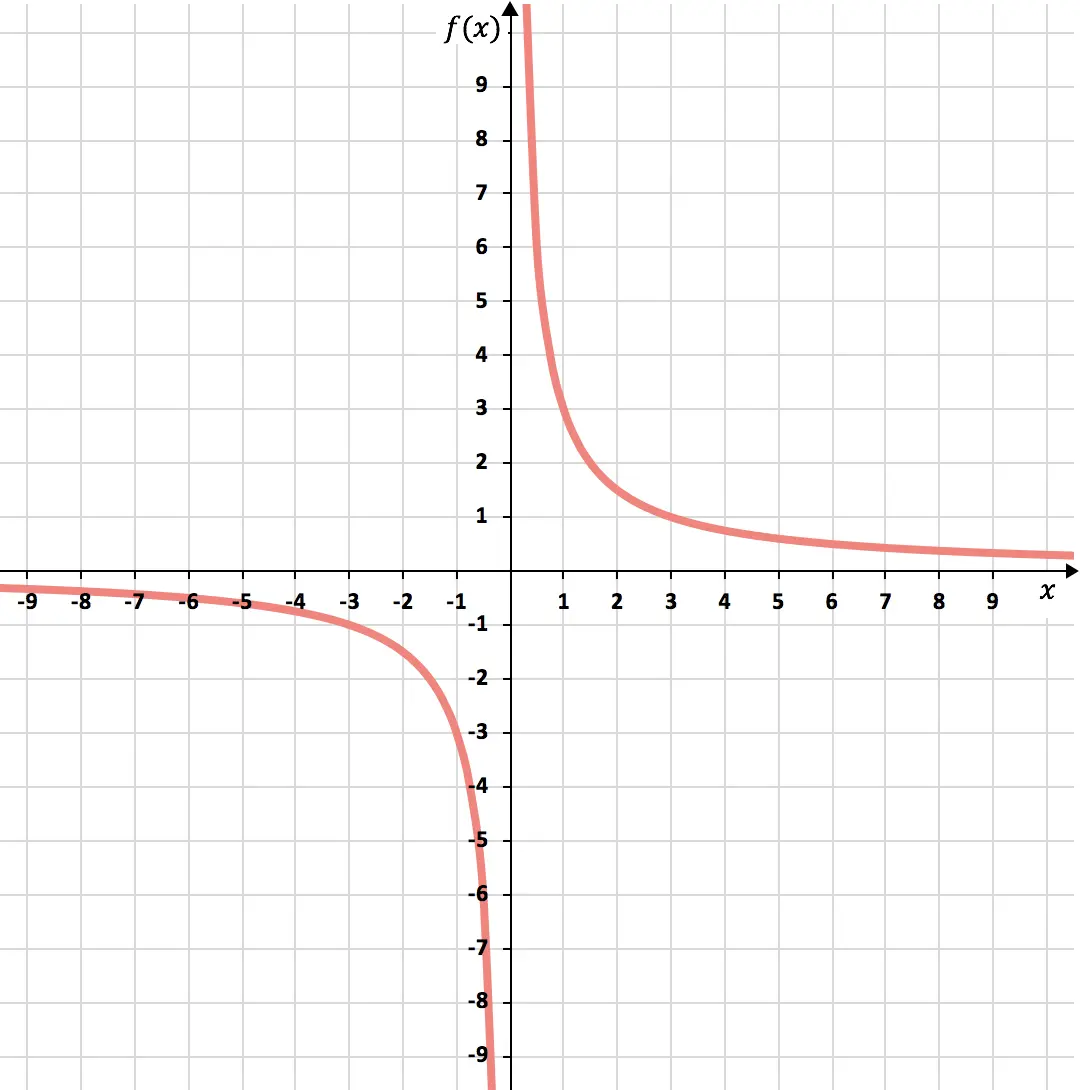
Oefening 3
Grafiek van de volgende inverse evenredigheidsfunctie:
![]()
Het eerste dat u moet doen, is het domein van de functie berekenen:
![]()
![]()
![]()
Zodra we het domein van de functie kennen, construeren we een tabel met waarden:

Ten slotte geven we de verkregen punten weer in een grafiek en plotten we de hyperbolen, waardoor we de inverse evenredigheidsfunctie vormen:
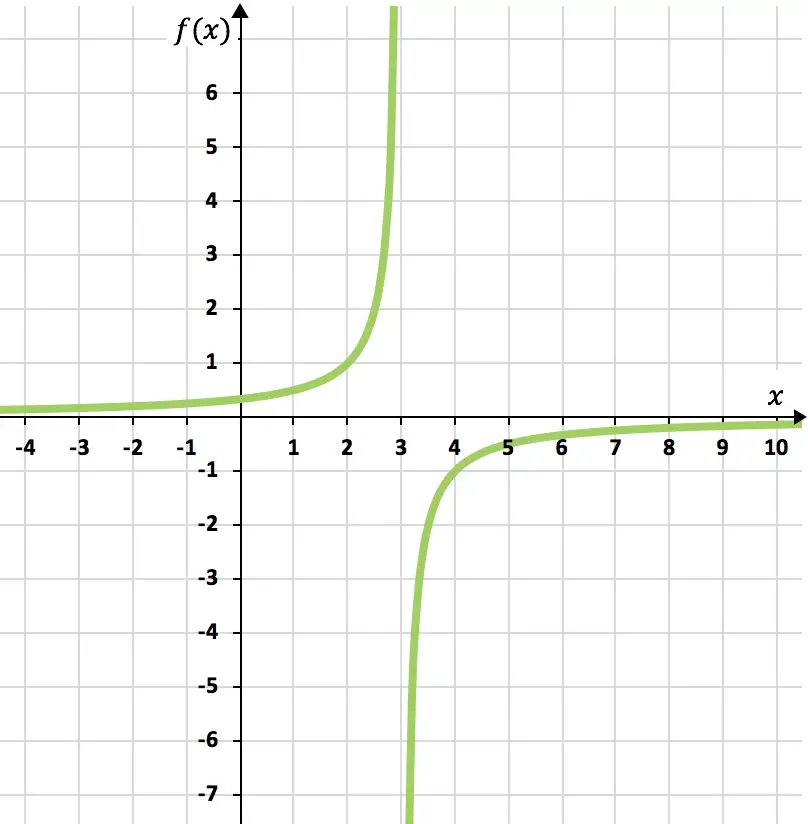
Oefening 4
Grafiek van de volgende inverse evenredigheidsfunctie:
![]()
Eerst moeten we het domein van de functie berekenen:
![]()
![]()
![]()
![]()
Zodra we het domein van de functie kennen, creëren we een array van waarden:
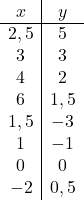
En ten slotte geven we de verkregen punten weer in een grafiek en tekenen we de hyperbolen, waardoor we de inverse evenredigheidsfunctie vormen:
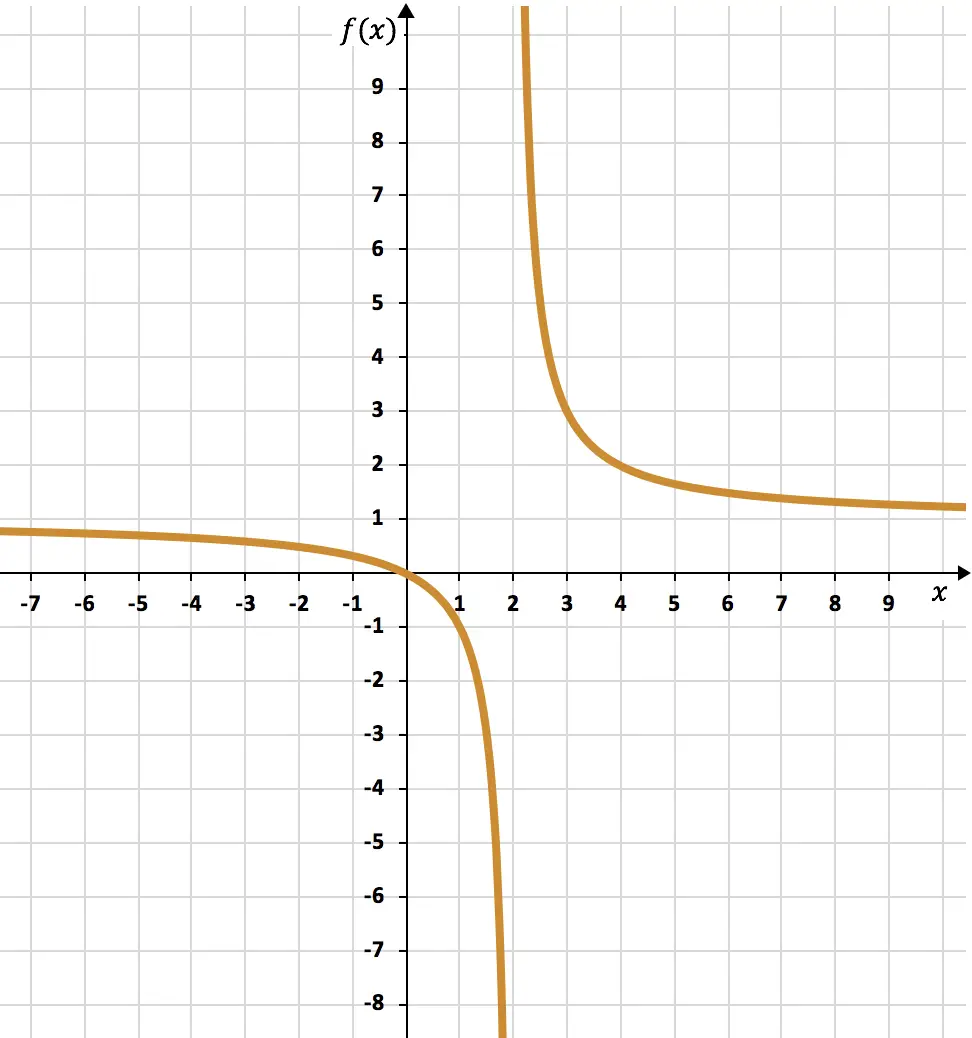
Oefening 5
Grafiek de volgende rationale functie:
![]()
Het eerste dat u moet doen, is het domein van de functie berekenen:
![]()
![]()
![]()
![]()
Zodra we het domein van de functie kennen, construeren we een tabel met waarden:

Om te eindigen, geeft u eenvoudigweg de verkregen punten weer in een grafiek en tekent u de hyperbolen, waardoor de breukfunctie ontstaat:

Toepassingen van de inverse evenredigheidsfunctie
De inverse evenredigheidsfunctie komt in veel gevallen voor in de natuurkunde en wiskunde.
Het wordt bijvoorbeeld gebruikt om de relatie tussen druk en volume te beschrijven in een ideaal gas onderworpen aan een constante temperatuur k. Deze functie wordt de wet van Boyle-Mariotte (P×V=k) genoemd en is een voorbeeld van een inverse evenredigheidsfunctie. Het is duidelijk dat het domein van de definitie van deze functie alleen beperkt is tot de positieve tak, aangezien er geen negatieve volumes of drukken zijn.
De relatie tussen de stroomsterkte en de elektrische weerstand die onderhevig is aan een constant potentiaalverschil, wordt ook bepaald door een omgekeerde evenredigheidsfunctie. Deze functie staat bekend als de wet van Ohm (V=I×R).