Hier vindt u de uitleg van wat ze zijn en hoe ze alle delen van een polynoom worden genoemd (graad, variabelen, onafhankelijke term, enz.). Daarnaast kun je verschillende voorbeelden bekijken en delen van een polynoom oefenen met opgeloste oefeningen.
Maar voordat we zien wat alle delen van een polynoom zijn, moeten we snel de wiskundige definitie ervan bekijken om het concept volledig te begrijpen: een polynoom is een algebraïsche uitdrukking die wordt gevormd door het optellen of aftrekken van monomialen van verschillende graden.
Wat zijn de delen van een polynoom?
De delen van een polynoom zijn:
- Termen : elk monomiaal deel van de polynoom.
- Coëfficiënten : de getallen die bij elke term van de polynoom horen.
- Graad : de grootste exponent waartoe de polynomiale variabele wordt verhoogd.
- Variabele : is de letter die de polynoom heeft.
- Hoofdterm : is de term van de hoogste graad van de polynoom.
- Onafhankelijke term : term van de polynoom die geen variabele bevat.
- Dominante coëfficiënt : coëfficiënt van de dominante term van de polynoom.
Wanneer de polynoom slechts één variabele heeft, is de graad ervan gelijk aan de grootste exponent van zijn termen. Als de polynoom echter twee of meer variabelen heeft, is het moeilijker om de graad ervan te kennen, aangezien er een bewerking moet worden uitgevoerd. Ontdek hoe dit gebeurt door op de volgende link te klikken voor de graad van een polynoom van twee (of meer) variabelen .
Hoe de delen van een polynoom te identificeren
De delen of elementen van een polynoom kunnen gemakkelijk visueel worden gevonden. Hoe dit wordt gedaan, ziet u in het volgende diagram:
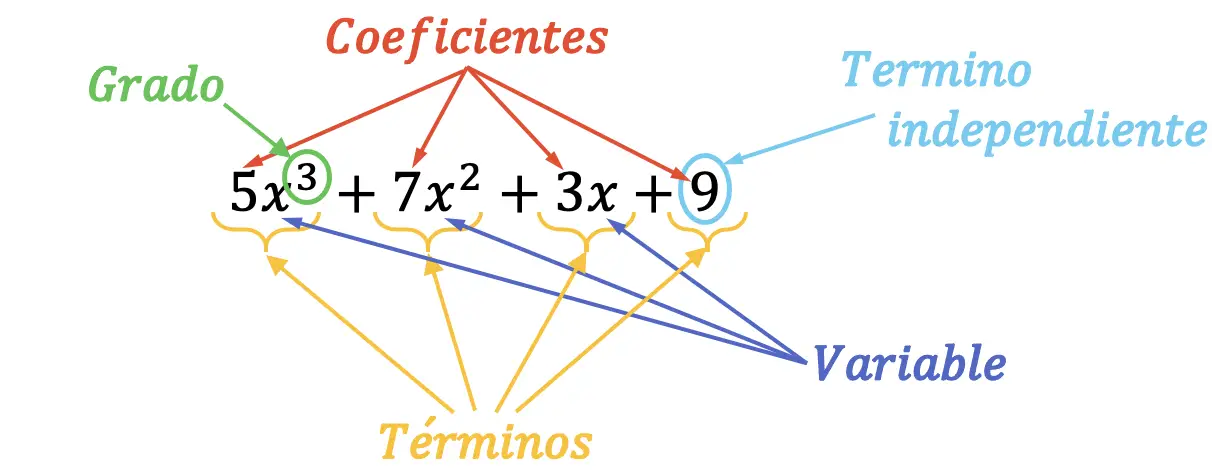
Van de vorige polynoom, die van de derde graad is, zijn alle delen gemarkeerd. Bovendien is de hoofdterm van genoemde polynoom ongeveer 5×3 , omdat dit de monomial van de hoogste graad is. Op dezelfde manier is de leidende coëfficiënt van de polynoom 5, aangezien dit de coëfficiënt van de eerste term is.
In dit geval heeft de polynoom één enkele variabele en heeft daarom slechts één type graad. Maar u moet weten dat wanneer de polynoom multivariabel is, u onderscheid moet maken tussen de absolute graad en de relatieve graad van een variabele. Je kunt zien waar elk van hen uit bestaat in de link die ik je hierboven heb achtergelaten ⬆⬆ ( graad van een polynoom van twee variabelen ).
Voorbeelden van delen van een polynoom
Om de betekenis van de delen van een polynoom en de functie die ze vervullen te begrijpen, zullen we enkele voorbeelden zien van het bepalen van de delen van elk type polynoom:
voorbeeld 1
Identificeer de delen van het volgende kwadratische (graad 2) polynoom:
![]()
- Voorwaarden: 4x 2 , -8x, 1
- Coëfficiënten: 4, -8, 1
- 2e jaar
- Variabel: x
- Hoofdtermijn: 4x 2
- Onafhankelijk mandaat: 1
- Stuurcoëfficiënt: 4
Aan de andere kant moet worden opgemerkt dat de polynoom in dit voorbeeld een trinominaal wordt genoemd. Je kunt zien wat dit type polynoom is in voorbeelden van trinomialen . Bovendien ben je misschien ook geïnteresseerd in een ander type polynoom, genaamd binomiaal (het is gemakkelijker om er bepaalde bewerkingen mee uit te voeren). Je kunt zien wat er speciaal aan is in binomiale voorbeelden .
Voorbeeld 2
Zoek de delen van de volgende polynoom:
![]()
- Voorwaarden: y 3 , 9y 2 , -5y, 3
- Coëfficiënten: 1, 9, -5, 3
- 3e jaar
- variabelen: en
- Hoofdterm: en 3
- Onafhankelijk mandaat: 3
- Stuurcoëfficiënt: 1
Zoals je in dit voorbeeld kunt zien, betekent het dat als er geen getal voor staat, de coëfficiënt één is. De leidende coëfficiënt van deze polynoom is dus gelijk aan 1.
Opgeloste oefeningen van de delen van een polynoom
Om je te helpen de namen van alle delen van een polynoom te onthouden, hebben we verschillende opgeloste oefeningen voor je voorbereid. In de reacties kunt u ons al uw vragen hierover stellen. ⬇⬇
Oefening 1
Zoek alle delen van de volgende polynoom:
![]()
De polynoom in deze oefening heeft geen onafhankelijke term, aangezien alle termen worden gevormd door ten minste één variabele (of letter).
Voorwaarden: 2×4 , 6×2 , x
Coëfficiënten: 2, 6, 1
Niveau 4
Variabel: x
Hoofdterm: 2×4
Onafhankelijke term: niet
Stuurcoëfficiënt: 2
Oefening 2
Zoek alle delen van de volgende polynoom:
![]()
De polynoom in dit probleem bestaat uit twee variabelen: x en y. Nog:
Voorwaarden: -7x 4 y 2 , 3x 4 , -5y 2 , xy, -10
Coëfficiënten: -7, 3, -5, 1, -10
6e jaar
Variabelen: x, y
Hoofdterm: -7x 4 en 2
Onafhankelijk mandaat: -10
Stuurcoëfficiënt: -7
Zoals u kunt zien, moet u, om dit soort polynomen op te lossen, weten hoe u de graad van een polynoom met meer dan één variabele kunt berekenen. Als je nog steeds niet zeker weet hoe je dit moet doen, raad ik je aan de link hierboven in Wat zijn de delen van een polynoom? te bekijken. ( graad van een polynoom van twee variabelen ). ⬆⬆ Je vindt de stap-voor-stap uitleg en diverse voorbeelden.
Hoewel het een radicaal ander concept is, zul je, als je zo ver bent gekomen, zeker ook geïnteresseerd zijn om te weten wat de polynomiale uitdrukking van een getal is. Dit is iets dat niet veel mensen weten, maar dat eigenlijk heel nuttig is.